Ylin's Blog
0%

104:初始图形学(15)

发表于 更新于 分类于 ，
本文字数： 8.3k 阅读时长 ≈ 30 分钟

上一章中完成了对图形渲染的饿BVH加速，现在我们要尝试将图片纹理映射到物体中。

纹理映射

图形学中的纹理映射是将材质效果应用于场景中的物理过程。其中”纹理”指的是效果（这个效果可以是材质属性，或是部分存在与否）本身，而映射则是将效果映射到物体的表面上。

最为常见的纹理映射就是将图像映射到物体表面上，就像是把世界地图依附到球体表面。和我们的直觉不同，纹理映射是一个逆向的过程，我们首先确定物体上的一个点，然后查找纹理贴图给定的颜色，以实现对图片的映射。

不过在此之前，我们先用程序化的方式生成纹理颜色，并创建一个纹理贴图。为了执行纹理查找，我们需要物体表面的纹理坐标(u,v)以定位纹理中的像素，同时也需要保存当前点的三维坐标（部分纹理需要这一部分的信息）

恒定色彩纹理

我们的纹理颜色类将从最简单的恒定色彩纹理开始实现，实际上我们可以将物体的颜色也视作一种纹理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#ifndef TEXTURE_H
#define TEXTURE_H

#include "utils.h"

class texture{
    public:
        virtual ~texture() = default;
        virtual color value(double u, double v, point3& p) const = 0;
};
class solid_color : public texture{
    public:
        solid_color(const color& albedo) : albedo(albedo) {}

        solid_color(double red, double green, double blue) : solid_color(color(red,green,blue)) {}

        color value(double u, double v, point3& p){
            return albedo;
        }
    private:
        color albedo;
};

#endif

这里我们先实现对纹理类的接口的一个实现，然后创建一个恒定色彩纹理类，返回恒定的颜色类型。

注意到我们这里需要使用到(u,v)表面坐标，我们还需要更新hit_record结构，对这些射线碰撞信息进行存储：

1
2
3
4
5
6
7
8
class hit_record {
public:
    point3 p;
    double u;
    double v;
    vec3 normal;
	...
};

棋盘纹理

棋盘纹理作为实体纹理中的一种。实体纹理取决点在空间中的位置，我们可以理解为给空间中的指定点进行着色，而不是给空间中的某个物体上色。正因如此，当我们的物体在空间中移动时，纹理并不会随物体进行移动，反而像是物体在穿过纹理。

这里我们将实现一个棋盘纹理类，它是一种空间纹理（即实体纹理）。根据点在空间中给定的位置进行纹理颜色的渲染。

为了实现棋盘格图案，我们需要对当前点的每个坐标分量取floor，这样我们就将整个空间分割为1x1x1的单元格，每个坐标都可以映射到对应的单元格，我们对奇数的单元格赋予一种颜色，对偶数赋予另外的一种颜色，这样就实现了棋盘的样式。同时我们还可以设置一个缩放因子scale，控制单元格的大小，从而实现对棋盘格的大小控制：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class checker_texture : public texture{
    public:
        checker_texture(double scale, shared_ptr<texture> even, shared_ptr<texture> odd)
            : inv_scale(1.0/scale), even(even), odd(odd) {}

        checker_texture(double scale, const color& c1, const color& c2)
            : checker_texture(scale, make_shared<solid_color>(c1), make_shared<solid_color>(c2)) {}

        color value(double u, double v, point3& p) const override{
            auto xInt = int(floor(inv_scale*p.x()));
            auto yInt = int(floor(inv_scale*p.y()));
            auto zInt = int(floor(inv_scale*p.z()));

            bool isEven = (xInt + yInt + zInt) % 2 == 0;

            return isEven ? even->value(u,v,p) : odd->value(u,v,p);
        }

    private:
        double inv_scale;
        shared_ptr<texture> even;
        shared_ptr<texture> odd;
};

为了进一步的支持纹理，我们拓展lambertian类，使用纹理代替颜色：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class lambertian : public material {
public:
    lambertian(const color& albedo) : tex(make_shared<solid_color>(albedo)) {}

    lambertian(shared_ptr<texture> tex) : tex(tex) {}

    virtual bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) override {
        auto scatter_direction = rec.normal + random_unit_vector();
        if (scatter_direction.near_zero()) {
            scatter_direction = rec.normal;
        }
        scattered = ray(rec.p, scatter_direction, r_in.time());
        attenuation = tex->value(rec.u, rec.v, rec.p);
        return true;
    }

private:
    shared_ptr<texture> tex;
};

这里通过多态的思想实现了对lambertian材质的纹理的实现。

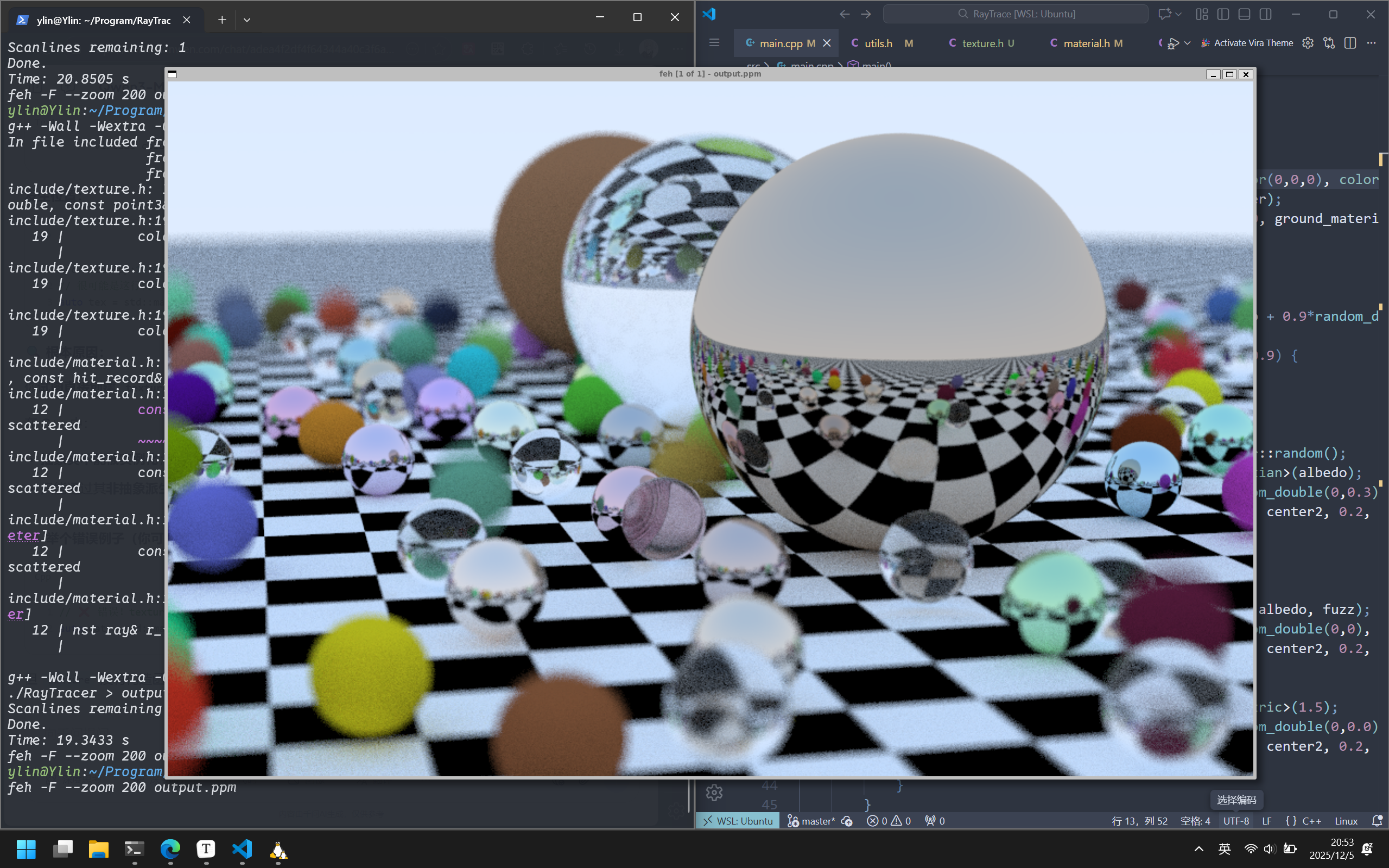
现在我们可以向我们的场景中添加纹理了：

1
2
3
4
   // main.cpp中将地面设置成棋盘样式
auto checker = make_shared<checker_texture>(0.2, color(0,0,0), color(1,1,1));
   auto ground_material = make_shared<lambertian>(checker);
   world.add(make_shared<sphere>(point3(0,-1000,0), 1000, ground_material));

渲染结果如下：

image.png

空间纹理的特殊情况

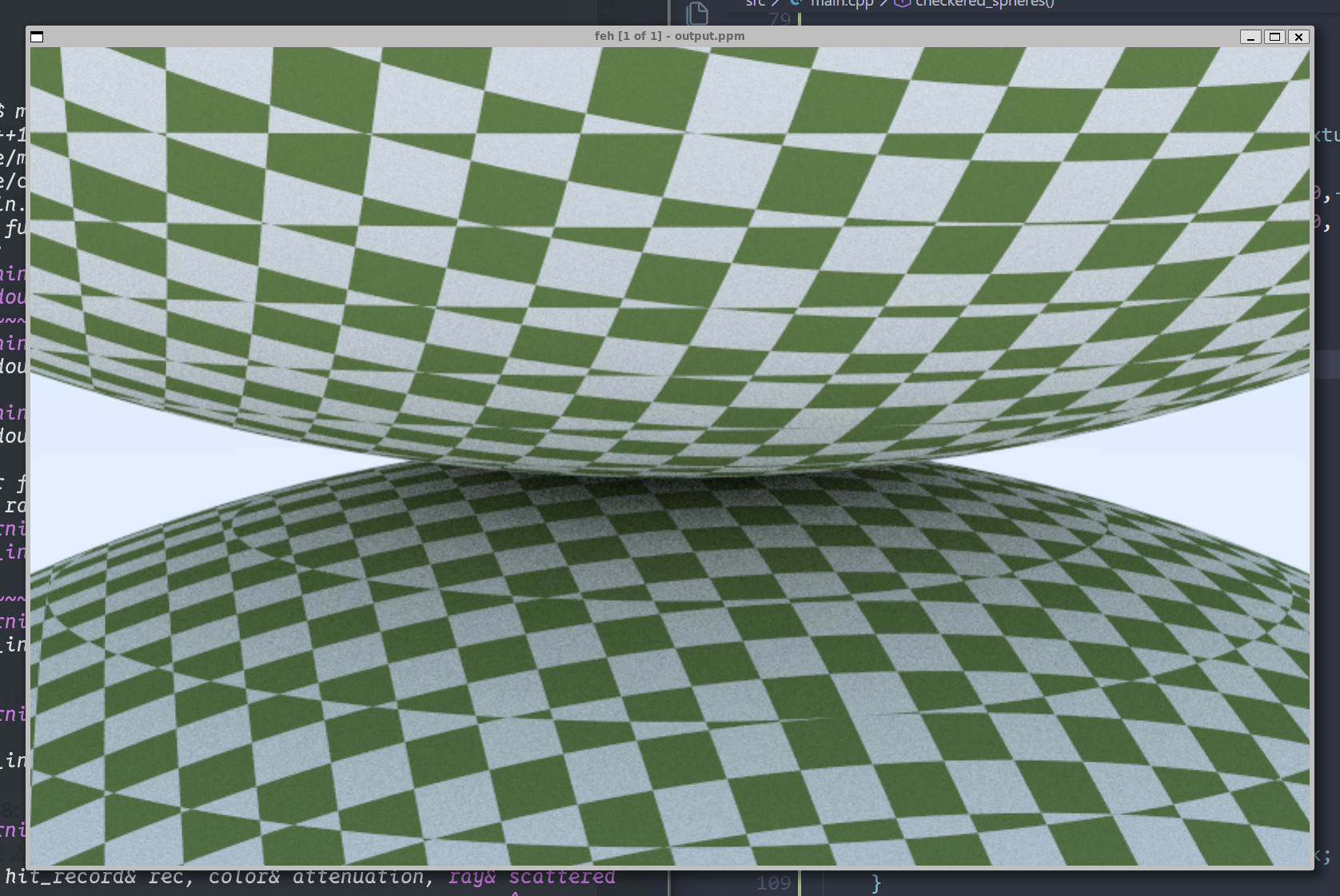
正如之前所提到的，这种实体纹理的上色方式，更像是物体在穿过纹理，从而完成上色。

我们现在创建一个新的场景来观察这种特殊的情况，我们将先前的main函数保存为一个bounding_ball场景，然后现在我们再来创建一个新的场景：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void checkered_spheres() {
    hittable_list world;

    auto checker = make_shared<checker_texture>(0.32, color(.2, .3, .1), color(.9, .9, .9));

    world.add(make_shared<sphere>(point3(0,-10, 0), 10, make_shared<lambertian>(checker)));
    world.add(make_shared<sphere>(point3(0, 10, 0), 10, make_shared<lambertian>(checker)));

    camera cam;

    cam.aspect_ratio      = 25.0 / 16.0;
    cam.image_width       = 800;
    cam.samples_per_pixel = 100;
    cam.max_depth         = 50;

    cam.vfov     = 20;
    cam.lookfrom = point3(13,2,3);
    cam.lookat   = point3(0,0,0);
    cam.vup      = vec3(0,1,0);

    cam.defocus_angle = 0;

    cam.render(world);
}

我们通过main函数中的switch来切换我们想要渲染的场景：

1
2
3
4
5
6
int main(){
    switch(2){
        case 1: bounding_ball(); break;
        case 2: checkered_spheres(); break;
    }
}

我们渲染出来的结果如下：

image.png

这就是空间纹理渲染的特殊情况，不过你应该能理解这是什么情况。所以为了解决这个问题，我们需要使用表面纹理，这就意味着我们需要根据(u,v)的球体表面位置信息来创建纹理。

球体表面纹理坐标

空间纹理通过空间中一点的坐标，实现纹理的绘制。但是真如我们先前所提到的空间纹理的局限性，我们希望能够更具球体表面的坐标实现对图像点对点的映射。这就以为着我们需要一种方法来查找三维球体表面任意点的坐标(u,v)。

这里用到一个经纬度的思想，首先确定出这个点在球体上的经纬度(θ, ϕ)（横纬竖经，这里θ从-Y向上，ϕ从-X到+Z到+X到-Z），然后再将球面坐标表示出来，这里的话，如果学过球面坐标，自然能够得到以下式子： $$ 我们可以简单的推导得到： $$ 所以我们可以写出sphere类中的get_uv方法：

1
2
3
4
5
6
static void get_uv(const point3& p, double& u, double& v){
    auto theta = std::acos(-p.y());
    auto phi = std::atan2(-p.z(),p.x()) + pi;
    u = phi / (2*pi);
    v = theta / pi;
}

然后我们向hit方法中添加，每次碰撞记录的(u,v):

1
2
3
4
5
6
7
8
9
10
11
  bool hit(const ray& r, interval t_range, hit_record& rec) const override {
...
      rec.t = root;
      rec.p = r.at(rec.t);
      vec3 outward_normal = (rec.p - cur_center) / radius;
      rec.set_face_normal(r, outward_normal);
      // 这里的outward 就是从球心指向碰撞点的向量
      get_uv(outward_normal,rec.u,rec.v);
      rec.mat = mat;
      return true;
  }

现在我们就实现了对球体表面的位置的(u,v)二维定位

访问纹理图像数据

现在我们需要一种手段，将图片数据解析为一种二维关系，我们希望通过(u,v)访问图像数据上对应的像素值。所以我们需要将图片加载为一个浮点数数组，便于我们访问。这里我们使用第三方库stb_image.h来实现

首先我们创建一个辅助类来帮助我们管理图片信息内容，以提供一个pixel_data(int x,int y)方法，来访问任意像素的8位（unsigned char）RGB。

我们的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#ifndef IMAGE_H
#define IMAGE_H

#ifdef _MSC_VER
    #pragma warning (push,0)
#endif

#define STB_IMAGE_IMPLEMENTATION
#define STBI_FAILURE_USERMSG

#include "stb_image.h"
#include "utils.h"

class image{
    public:
        image(){}

        image(const char* image_file){
            auto filename = std::string(image_file);
            if(load("../images/" + filename)) return;

            std::cerr << "ERROR: Could not load image file" << image_file << "\n";
        }

        ~image(){
            delete[] bdata;
            STBI_FREE(fdata);
        }

        bool load(const std::string& filename){
            auto n = bytes_per_pixel;
            fdata = stbi_loadf(filename.c_str(), &image_width, &image_height, &n, bytes_per_pixel);
            if(fdata == nullptr) return false;

            byte_per_scanline = bytes_per_pixel * image_width;
            convert_to_bytes();
            return true;
        }

        int width() {return (fdata==nullptr) ? 0 : image_width;}
        int height() {return (fdata==nullptr) ? 0 : image_height;}

        const unsigned char* pixel_data(int x, int y) const{
            static unsigned char magenta[] = {255,0,255};
            if(bdata==nullptr) return magenta;

            x = clamp(x,0,image_width);
            y = clamp(y,0,image_height);

            return bdata + x*bytes_per_pixel + y*byte_per_scanline;
        }

    private:
        const int bytes_per_pixel = 3;      // 每像素的位数(即通道数)
        float* fdata = nullptr;             // 浮点像素数据
        unsigned char* bdata = nullptr;     // 8bit像素数据
        int image_width = 0;                // 图像宽度
        int image_height = 0;               // 图像高度
        int byte_per_scanline = 0;          // 宽的像素数量

    	// return [low,high)
        static int clamp(int x, int low, int high){
            if(x < low) return low;
            if(x < high) return x;
            return high - 1;
        }

        static unsigned char float_to_byte(float value){
            if(value <= 0.0)
                return 0;
            if(value >= 1.0)
                return 255;
            return static_cast<unsigned>(value*256.0);
        }

        void convert_to_bytes(){
            int total_bytes = bytes_per_pixel * image_height * image_width;
            bdata = new unsigned char[total_bytes];

            auto *bptr = bdata;
            auto *fptr = fdata;
            for(auto i=0; i<total_bytes ; i++,fptr++,bptr++)
                *bptr = float_to_byte(*fptr);
        }
};


#ifdef _MSC_VER
    #pragma warning (pop)
#endif

#endif

现在我们封装好了一个加载并获取图像内容的image类，我们可以利用它实现图像纹理image_texture:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class image_texture : public texture{
    public:
        image_texture(const char* filename) : image(filename){}

        color value(double u, double v, const point3& p) const override{
            if(image.height() <= 0) return color(0,1,1);

            u = interval(0,1).clamp(u);
            // 由于图片坐标起始位置是从左上角开始
            // 而图形学坐标从左下角开始,所以需要进行反转
            v = 1.0 - interval(0,1).clamp(v);
            
            auto i = int(u*image.width());
            auto j = int(v*image.height());
            auto pixel = image.pixel_data(i,j);

                    auto color_scale = 1.0 / 255.0;
        return color(color_scale*pixel[0], color_scale*pixel[1], color_scale*pixel[2]);
        }

    private:
        image image;
};

图像纹理渲染

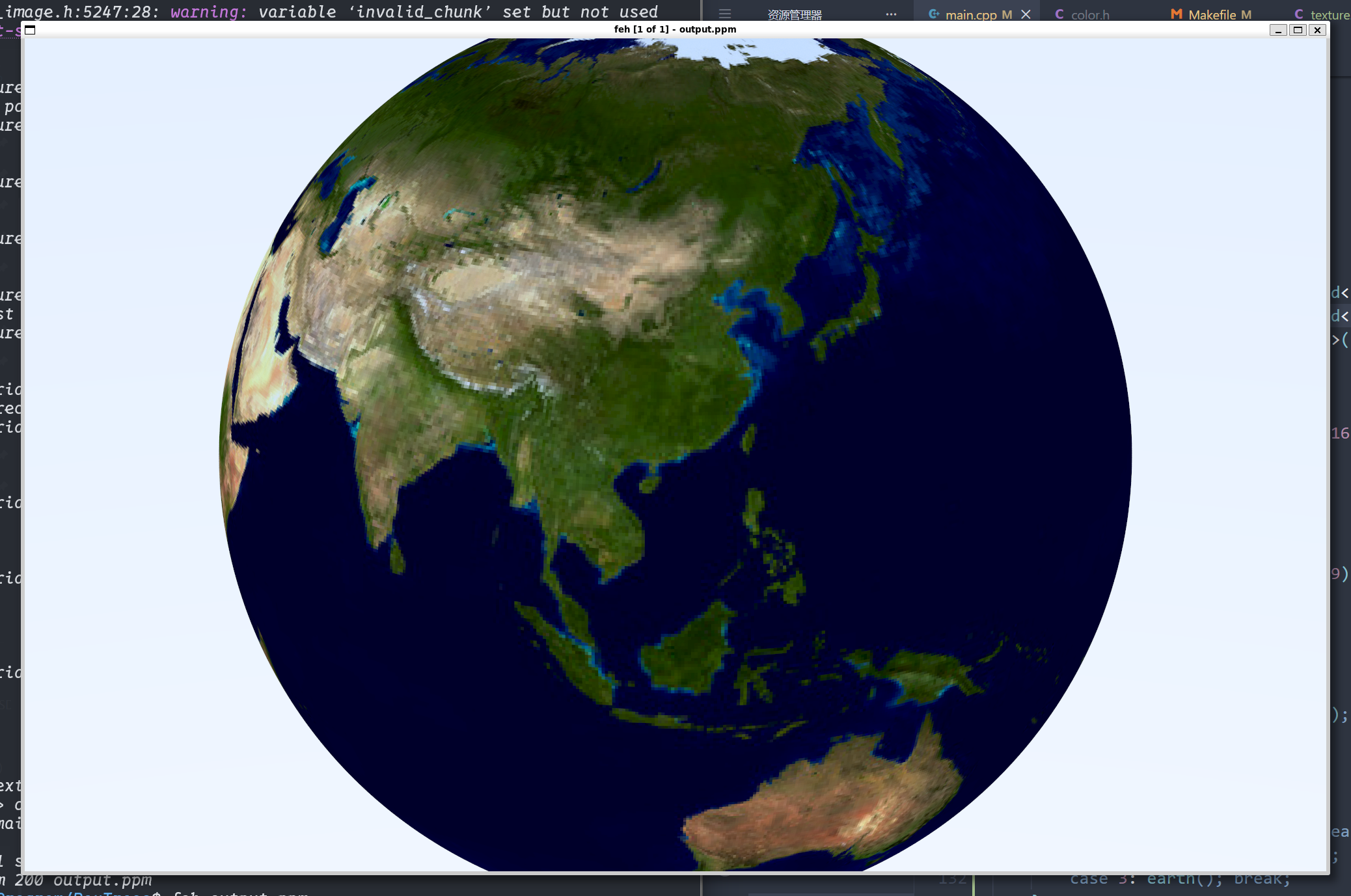
现在我们可以尝试将一个图片进行渲染：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void earth() {
    auto earth_texture = make_shared<image_texture>("earthmap.jpg");
    auto earth_surface = make_shared<lambertian>(earth_texture);
    auto globe = make_shared<sphere>(point3(0,0,0), 2, earth_surface);

    camera cam;

    cam.aspect_ratio      = 25.0 / 16.0;
    cam.image_width       = 2000;
    cam.samples_per_pixel = 100;
    cam.max_depth         = 10;

    cam.vfov     = 20;
    cam.lookfrom = point3(-3.75,4,-9);
    cam.lookat   = point3(0,0,0);
    cam.vup      = vec3(0,1,0);

    cam.defocus_angle = 0;

    cam.render(hittable_list(globe));
}

我们使用一张地球的贴图（效果如下）：

image.png

至此 我们的纹理样式就简单介绍完了