Ylin's Blog
0%

103:初始图形学(14)

发表于 更新于 分类于 ，
本文字数： 3.1k 阅读时长 ≈ 11 分钟

书接上回，上一次实现了物体运动下的图形学渲染。实现了动态模糊的构建。

包围体积层级

现在随着我们场景的复杂化，和对图片质量的提升，有时候渲染一张照片都需要十几分钟。为了让代码运行的更快，我们需要引入一个新的结构 包围体积层级BVH，以优化程序渲染的性能。

射线 - 对象求交，是光线追踪过程中的主要性能瓶颈，运行的时间和物体的数量呈线性关系。每当我们发射一条射线，就需要对场景内的所有物体进行求交判断。但是实际上和很多物体的求交是没有必要的，我们向天空发射的一条光线并不会和地上的物体有所交集。

所以我们为了优化这个过程，我们需要避免不必要的射线 - 对象求交计算，接下来我们要学习的方法就是通过包围体积层次来实现对求交场景的优化。

关键思想

为一组对象创建一个完全包围所有对象的包围盒，假如射线会错过这个包围盒，那么它一定会错过这个包围盒中的所有物体，反之，则有可能击中盒中的任意一个对象，所以我们的思想如下：

1
2
3
4
if(ray hits bounding object)
    return whether ray hits bounded objects
else
    return false

包围体积的层级

为了提高计算的效率，使得处理时间的增长速度慢于物体数量的增长。首先我们需要构建有一个层次化的包围体结构，这里我们通过自顶向下的方法，生成我们的包围体积的层级结构。

一开始我们需要构建一个层次化的包围体结构，用大的包围体包住一群物体，再逐层细化，就像下面这样：

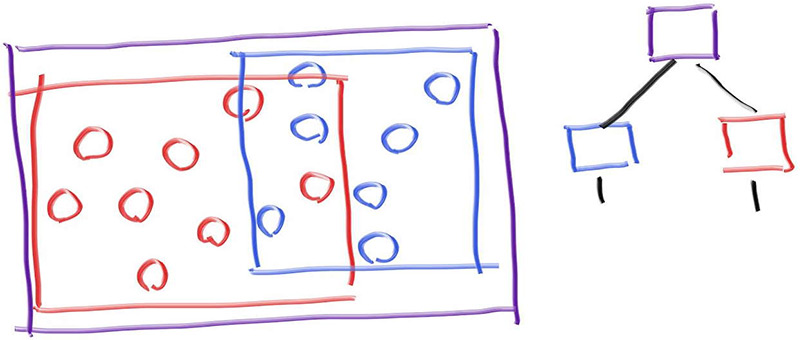image.png

我们可以写出以下伪代码：

1
2
3
4
5
6
if(hit purple)
    hit0 = hits blue enclosed objects
    hit1 = hits red enclosed objects
    if(hit0 or hit1)
        return true and info of closer hit
return false

当我们确定击中紫色包围盒时，分别对里面的蓝色组和红色组进行分析，从而进一步缩小碰撞检测的范围

轴对齐边界框(AABBs)

要让整个层次结构高效工作，我们需要要一个好的划分方式，而且我们需要一个较快的检测光线和包围体相交的算法，否则我们检测相交的速度会抵消掉包围结构层次带来的加速效果。这里我们选择轴对齐包围盒作为我们的包围体。我们通常将其称为AABB。

接下来我们需要了解光线和AABB相交检测的slab方法：

首先我们需要知道什么是片层(Slab)，片层是在一个坐标轴方向上，由两个平行平面围成的空间区域，比如在 x 轴方向，若 AABB 的 x 范围是 [x_min, x_max]，那么这个 slab 就是所有满足 x_min ≤ x ≤ x_max 的点。在我们要用到的3D场景中，AABB = x-slab && y-slab && z-slab。

理解片层之后，我们检测碰撞的关键就在于计算光线和不同片层之间的交点，其中射线的函数定于为P(t) = Q + td，我们可以求出其在x = x0t平面的交点为： $$ \begin{align*} x_0 &= Q_x + t_0d_x \\ t_0 &= \frac{x_0 - Q_x}{d_x} \\ t_1 &= \frac{x_1 - Q_x}{d_x} \end{align*} $$ 知道光线与各个片层之间的交点之后，我们可以进一步判断光线和AABB的相交情况了，以下图为例：

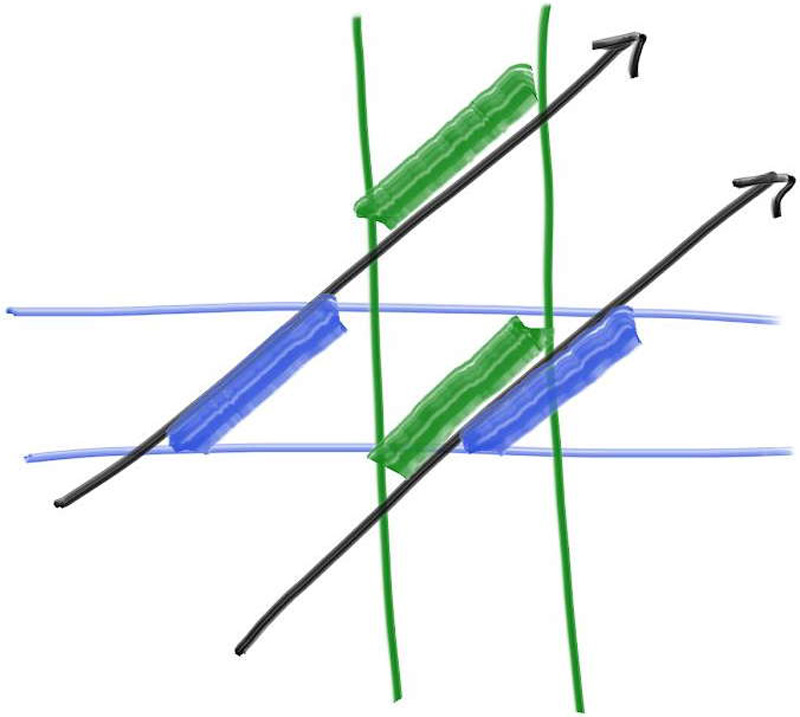image.png

这是一个二维的AABB场景，上面的射线和x、y片层中的交集段并没有重叠，所以我们知道射线并没有和AABB发生交集，下面的射线和x、y片层的交集段发生了重叠，所以说射线和AABB之间是有交集的。

与AABB的射线交

上图我们可以用于以下伪代码确定射线是否和AABB发生碰撞：

1
2
3
interval_x <- compute_intersection_x(ray, x0, x1)
interval_y <- compute_intersection_y(ray, y0, y1)
return overlaps(interval_x, interval_y)

相应的三维版本如下：

1
2
3
4
interval_x <- compute_intersection_x(ray, x0, x1)
interval_y <- compute_intersection_y(ray, y0, y1)
interval_z <- compute_intersection_z(ray, z0, z1)
return overlaps(interval_x, interval_y, interval_z)

我们已经知道了怎么求出射线和片层的相交区间，我们需要进一步的检测这些相交区间是否有交集，现在，我们的关键在于实现overlaps了，在此之前我们需要考虑以下几种特殊情况：

  • 如果射线沿着负x方向运动，我们的计算得到的区间会发生反转，所以我们始终需要根据min和max来标识我们的区间
  • 当dx为0 或接近0时，会求得t为-infinity/+infinity，我们通过min/max可以解决这个问题
  • 当dx为0 但Qx在AABB的界限上/界限内时，加缓冲防止边界问题

现在我们可以写出伪函数overlaps:

1
2
3
4
bool overlaps(t_interval1, t_interval2)
    t_min = max(t_interval.min, t_interval2.min)
    t_max = min(t_interval.max, t_interval2.max)
    return t_max>t_min

对于第三种特殊情况，此时我们无法给出准确的t_min和t_max，所以我们将这个情况称之为NaN，这里我们需要进行手动的处理，为区间添加一个padding，将NaN的情况视作fasle

为此我们需要为interval添加一个expend函数，它给区间填充给定的值：

1
2
3
4
5
6
7
8
9
10
class interval {
public:
	...
    interval expand(double delta) const{
        auto padding = delta/2;
        return interval(min-padding, max+padding);
    }
	...
    static const interval empty,universe;
};

现在，我们可以开始实现AABB类了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#ifndef AABB_H
#define AABB_H

#include "utils.h"

class aabb{
    public:
        interval x,y,z;

        aabb() {}   // 默认为空
        aabb(const interval& x, const interval& y, interval& z)
            : x(x), y(y), z(z) {}
        aabb(const point3& a, const point3& b){
            // 这里的a和b是AABB盒的对顶角
            x = (a[0]<=b[0]) ? interval(a[0],b[0]) : interval(b[0],a[0]);
            y = (a[1]<=b[1]) ? interval(a[1],b[1]) : interval(b[1],a[1]);
            z = (a[2]<=b[2]) ? interval(a[2],b[2]) : interval(b[2],a[2]);
        }

        const interval& axis_interval(int n)const{
            if(n==1) return y;
            if(n==2) return z;
            return x;
        }

        bool hit(const ray& r, interval ray_t) const{
            const point3& ray_orig = r.origin();
            const vec3& ray_dir = r.direction();

            for(int axis=0;axis<3;axis++){
                const interval& ax = axis_interval(axis);
                const double adinv = 1.0 / ray_dir[axis];

                auto t0 = (ax.min - ray_orig[axis]) * adinv;
                auto t1 = (ax.max - ray_orig[axis]) * adinv;
                
                // 收缩区间（取交集）
                if(t0 < t1){
                    if(t0 > ray_t.min) ray_t.min = t0;
                    if(t1 < ray_t.max) ray_t.max = t1;
                }else{
                    if(t1 > ray_t.min) ray_t.min = t1;
                    if(t0 < ray_t.max) ray_t.max = t0;
                }

                // 说明无交点
                if(ray_t.min >= ray_t.max)
                    return false;
            }
            return true;
        }
};

#endif

这里的关键在于hit函数，我们通过区间收缩的方式实现对交集的判断。

为可击中类创建包围盒

现在我们需要为所有的可击中类构建一个包围盒，对于单个的物体，我们将其包围盒视作包围结构层次中的叶子节点，这个我们之后会提到。

由于我们的物体有部分是动画的，所以我们为其生成的包围盒边界应该等于其运动范围，首先，我们需要升级我们的hittable类：

1
2
3
4
5
6
class hittable{
public:
    virtual ~hittable() = default;
    virtual bool hit(const ray& r, interval t_range, hit_record& rec) const = 0;
    virtual aabb bounding_box() const = 0;
};

对于静态和动态的球体，我们很容易为其创建出包围盒：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class sphere: public hittable {
public:
    // 静态球体
    sphere(const point3& static_center, double radius, shared_ptr<material> mat)
        : center(static_center,vec3(0,0,0)), radius(radius), mat(mat) {
            auto rvec = vec3(radius,radius,radius);
            bbox = aabb(static_center - rvec, static_center + rvec);
        }
    // 动态球体
    sphere(const point3& center1, const point3& center2, double radius, shared_ptr<material> mat)
        : center(center1,center2-center1), radius(radius), mat(mat) {
            auto rvec = vec3(radius,radius,radius);
            aabb box1(center.at(0) - rvec, center.at(0) + rvec);
            aabb box2(center.at(1) - rvec, center.at(1) + rvec);
            bbox = aabb(box1,box2);
        }
    
    aabb bounding_box() const override {return bbox;}

	...

private:
	...
    aabb bbox;
};

这里注意到我们直接将box1和box2合并成了一个新的包围盒区间，这是我们新定义的一种构造方法，也便于之后的包围盒合并：

1
2
3
4
5
6
7
8
9
10
   aabb(const aabb& box1, const aabb& box2){
       x = interval(box1.x, box2.x);
       y = interval(box1.y, box2.y);
       z = interval(box1.z, box1.z);
   }
// 这里用到的Interval合并形式，来自于interval类中新定义的合并构造
interval(const interval& a,const interval& b){
       min = a.min <= b.min ? a.min : b.min;
       max = a.max >= b.max ? a.max : b.max;
   }

创建对象列表的边界框

现在我们需要更新对象列表hittable_list，现在列表中的物体被创建时，会生成相应的包围盒边界。而我们需要随着每个新子节点的加入逐步的更新边界框，于是我们有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class hittable_list : public hittable {
private:
    aabb bbox;
public:
    std::vector<shared_ptr<hittable>> objects;
	....
    void add(shared_ptr<hittable> object) { 
        objects.push_back(object); 
        bbox = aabb(bbox,object->bounding_box());
    }
    aabb bounding_box() const override {return bbox;}

	....
};

BVH节点类

BVH本质上也是一个hittable ，它代表一组几何体，光线可以击中它以进行相交判断。我们将它视作一个对象的容器，它封装了几何体，通过包围盒相交测试进行加速检测。

我们通过一个类来实现它，它既可以是节点，也可以是整棵树的根：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#ifndef BVH_H
#define BVH_H

#include "AABB.h"
#include "hittable.h"
#include "hittable_list.h"
#include "utils.h"

class bvh_node: public hittable{
    public:
        bvh_node(std::vector<shared_ptr<hittable>>& objects, size_t start, size_t end) {
            // 待具体实现
        } 
        bvh_node(hittable_list list): bvh_node(list.objects, 0, list.objects.size()) {
            // 重载并使用了上面的初始化方法
        }

        bool hit(const ray& r, interval ray_t, hit_record& rec) const override{
            if(!bbox.hit(r,ray_t))
                return false;

            bool hit_left = left->hit(r, ray_t, rec);
            bool hit_right = right->hit(r, ray_t, rec);

            return hit_left||hit_right;
        }

        aabb bounding_box() const override{return bbox;}

    private:
        shared_ptr<hittable> left;
        shared_ptr<hittable> right;
        aabb bbox;
};

#endif

接下来的重点在于怎么将hittable_list构建成我们想要的BVH。我们希望每个BVH下至多有两个左右节点，但是我们以什么为依据进行划分呢，以下是我们的做法：

  • xyz轴任选其一
  • 根据轴值进行排序
  • 将子树对半存放

当我们构建BVH的递归生成时，会有以下几种情况：

  • list表中剩余一个物体，我们让BVH节点的子树均指向它
  • list表中剩余两个物体，我们让BVH节点的左右子树分别指向
  • list表中有两个以上物体，我们取一轴进行排序，递归进行生成BVH

因此，我们的BVH生成的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bvh_node(std::vector<shared_ptr<hittable>>& objects, size_t start, size_t end) {
    int axis = random_int(0,2);
    
    auto comparator = (axis==0) ? box_x_compare : (axis==1) ? box_y_compare : box_z_compare;

    size_t object_span = end - start;

    if(object_span == 1){
        left = right = objects[start];
    }else if(object_span == 2){
        left = objects[start];
        right = objects[start+1];
    }else{
        sort(std::begin(objects)+start, std::begin(objects)+end, comparator);
        auto mid = start + object_span/2;
        left = make_shared<bvh_node>(objects, start, mid);
        right = make_shared<bvh_node>(objects, mid, end);
    }
    bbox = aabb(left->bounding_box(), right->bounding_box());
}

这里sort使用的判断逻辑如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
static bool box_compare(
            const shared_ptr<hittable> a, const shared_ptr<hittable> b, int axis_index
        ) {
            auto a_axis_interval = a->bounding_box().axis_interval(axis_index);
            auto b_axis_interval = b->bounding_box().axis_interval(axis_index);
            return a_axis_interval.min < b_axis_interval.min;
        }

        static bool box_x_compare (const shared_ptr<hittable> a, const shared_ptr<hittable> b) {
            return box_compare(a, b, 0);
        }

        static bool box_y_compare (const shared_ptr<hittable> a, const shared_ptr<hittable> b) {
            return box_compare(a, b, 1);
        }

        static bool box_z_compare (const shared_ptr<hittable> a, const shared_ptr<hittable> b) {
            return box_compare(a, b, 2);
        }

不过实际上我们是可以对这一部分优化的。我们希望构造出来的BVH树是均衡的，所以每次对场景内的物体进行划分时，我们希望，左右子树的分布是均衡的，这就要求我们每次选择的检测轴应该是边长最长的轴。为此我们需要一个函数为我们计算出包围盒的范围，我们将以此为依据实现更加平衡的BVH树结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bvh_node(std::vector<shared_ptr<hittable>>& objects, size_t start, size_t end) {
            bbox = aabb::empty;
    		// 对区间内的所有包围盒取并集 
            for(size_t object_index = start; object_index < end; object_index++)
                bbox = aabb(bbox, objects[object_index]->bounding_box());
            // 选择边长最大的维度 作为划分轴
            int axis = bbox.longest_axis();
            
            auto comparator = (axis==0) ? box_x_compare : (axis==1) ? box_y_compare : box_z_compare;

            size_t object_span = end - start;

            if(object_span == 1){
                left = right = objects[start];
            }else if(object_span == 2){
                left = objects[start];
                right = objects[start+1];
            }else{
                sort(std::begin(objects)+start, std::begin(objects)+end, comparator);
                auto mid = start + object_span/2;
                left = make_shared<bvh_node>(objects, start, mid);
                right = make_shared<bvh_node>(objects, mid, end);
            }

            bbox = aabb(left->bounding_box(), right->bounding_box());
        }

为了实现对最长轴的判断 和 包围盒并集的实现，我们需要优化我们的aabb类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class aabb{
    public:
		...
		// 取最长轴
        int longest_axis() const {
            if(x.size() > y.size())
                return x.size() > z.size() ? 0 : 2;
            else
                return y.size() > z.size() ? 1 : 2;
        }
		// 空包围盒 与 无限包围盒
        static const aabb empty, universe;
};

const aabb aabb::empty = aabb(interval::empty, interval::empty, interval::empty);
const aabb aabb::universe = 
    aabb(interval::universe, interval::universe, interval::universe);

至此我们就实现了图形的加速渲染。太爽了。

速度差不多提升3-4倍，随着场景规模的提升，这个提升的效果更加明显，可以借下面这个图来感受一下。我们差不多实现了从O(n)到O(logn)的优化：

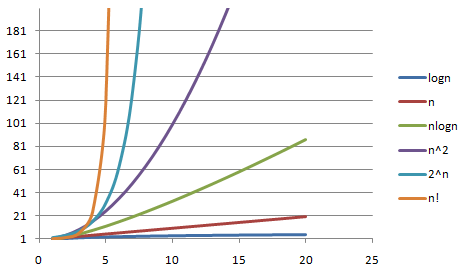image.png