Ylin's Blog
0%

99:图

发表于 更新于 分类于 ，
本文字数： 2.4k 阅读时长 ≈ 9 分钟

今天接着来认识一下图，结束了图的学习，数据结构的部分就告一段落了。之后就是涉及到一些基本的算法问题，感觉也会越来越难。

图

认识图

和之前的数据结构不同，图是一种非线性的结构，由顶点和边组成，以下面为例，我们可以将图G抽象的表示成一组顶点和一组边的集合：

1
2
3
V = {1,2,3,4,5}
E = {(1,2),(1,3),(1,5),(2,3),(2,4),(2,5),(4,5)}
G = {V,E}

如果将顶点看作节点，将边看作连接各个节点的引用（指针），我们就可以将图看作一种从链表拓展而来的数 据结构。

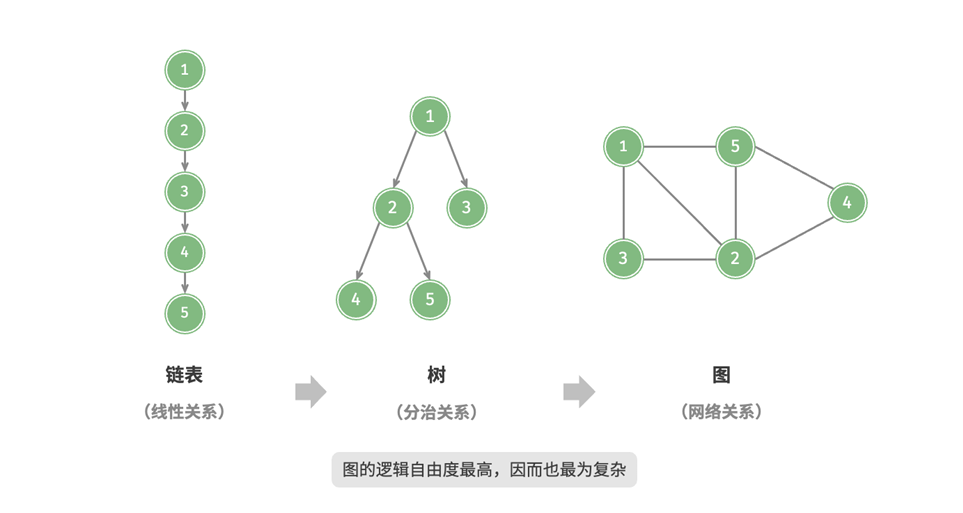image.png

图的常见类型和术语

结合不同的场景，我们可以从不同的角度对图进行分类：

  • 根据边是否具有方向，分为有向图和无向图
  • 根据顶点直接是否全部联通，分为联通图和非联通图
  • 根据边上的权重，非为无权图和有权图
  • ….

在不同的场景中我们选择合适的类型，来解决问题。

图的数据结构有以下常用术语：

  • 邻接：当两顶点之间存在边相连时，称这两个顶点邻接
  • 路径：从顶点A到顶点B经过的边构成的序列被称为从A到B的路径
  • 度：一个顶点拥有的边数。对有向图，根据边的方向，还分为入度和出度。

图的表示

图通常使用两种表示方式，我们这里均以无向图为例：

邻接矩阵

设图的顶点数量为𝑛，邻接矩阵使用一个n×n大小的矩阵来表示图，每一行（列）代 表一个顶点，矩阵元素代表边，用1或0表示两个顶点之间是否存在边。

设邻接矩阵为𝑀、顶点列表为𝑉 ，那么矩阵元素𝑀[𝑖,𝑗]=1表示顶点𝑉[𝑖]到顶点𝑉[𝑗] 之间存在边，反之𝑀[𝑖,𝑗]=0表示两顶点之间无边。

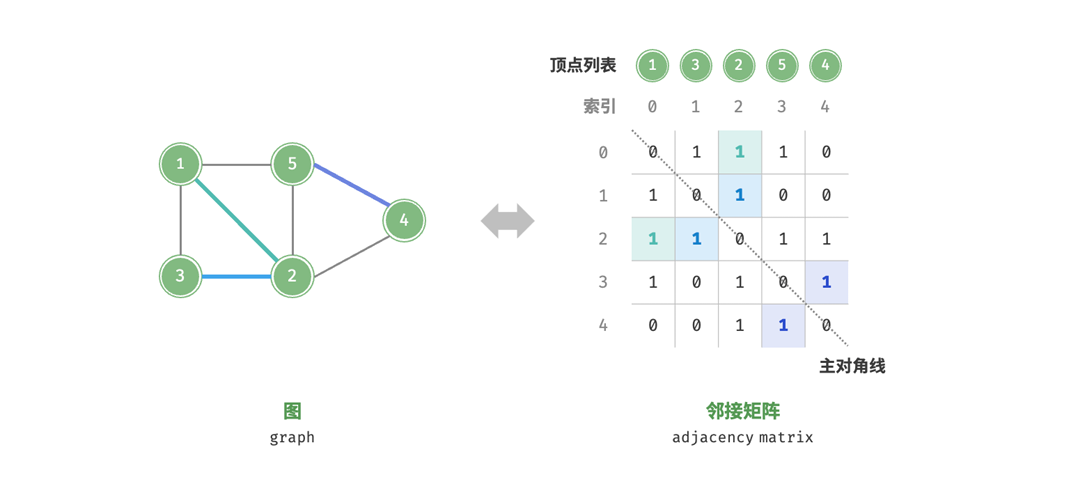image.png

邻接矩阵有以下性质：

  • 在简单图中，顶点不能和自己相连，所以邻接矩阵主对角线上的元素是没有意义的
  • 对于无向图，两个方向的边等价，此时邻接矩阵关于主对角线对称
  • 将邻接矩阵的元素替换成权重就是有权图

邻接表

邻接表使用n个链表来表示图，链表节点表示顶点。第i个链表对应顶点i，其中存储了该顶点的所有邻接顶点（与该顶点相连的顶点）。如下图：

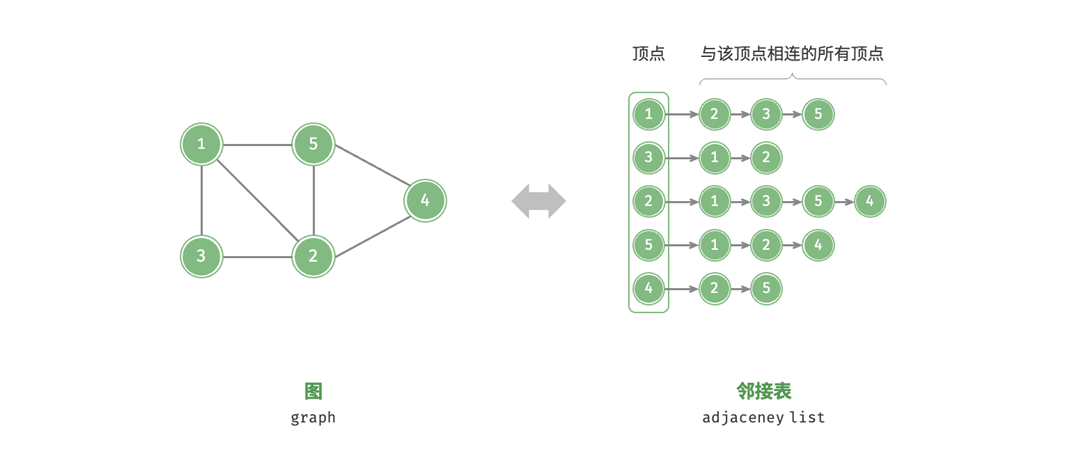image.png

两种表示方法的比较

对于邻接矩阵，我们可以直接访问矩阵元素实现对边的CRUD，时间效率高达O(1)。但是矩阵存储的空间复杂度为O(n2)

对于邻接表，由于表中只存储实际已存在的边数，而边数通常小于n2，所以空间存储的效率上来看，邻接表要更加的节省空间。但是对于CRUD的操作，邻接表需要通过遍历搜索的方式来进行，所以时间效率更差。

但是结合先前的只是，对于这种链表较长的情况，我们可以将它优化成哈希表或者AVL树等结构，实现对时间效率的优化，所以对于大规模的图的使用场景，邻接表也更加普遍。

图的基本操作

图的操作主要可以分为对顶点和对边的操作，这里分别通过邻接矩阵和邻接表的方式进行实现。

基于邻接矩阵的实现

给定给一个顶点数量为n的无向图，我们需要完成以下操作：

  • 添加或删除边：直接在邻接矩阵修改指定的边，只不过要注意同时更新两个方向的边（无向图）
  • 添加顶点：在邻接矩阵的尾部添加一行一列，并初始化为0即可。
  • 删除顶点：在邻接举证中删除一行一列，将剩下的元素向左上补齐。对于最坏的情况（删除首行首列）需要移动(n − 1)2个元素
  • 初始化：传入n个顶点，初始化长度为n的顶点列表和nxn大小的邻接矩阵
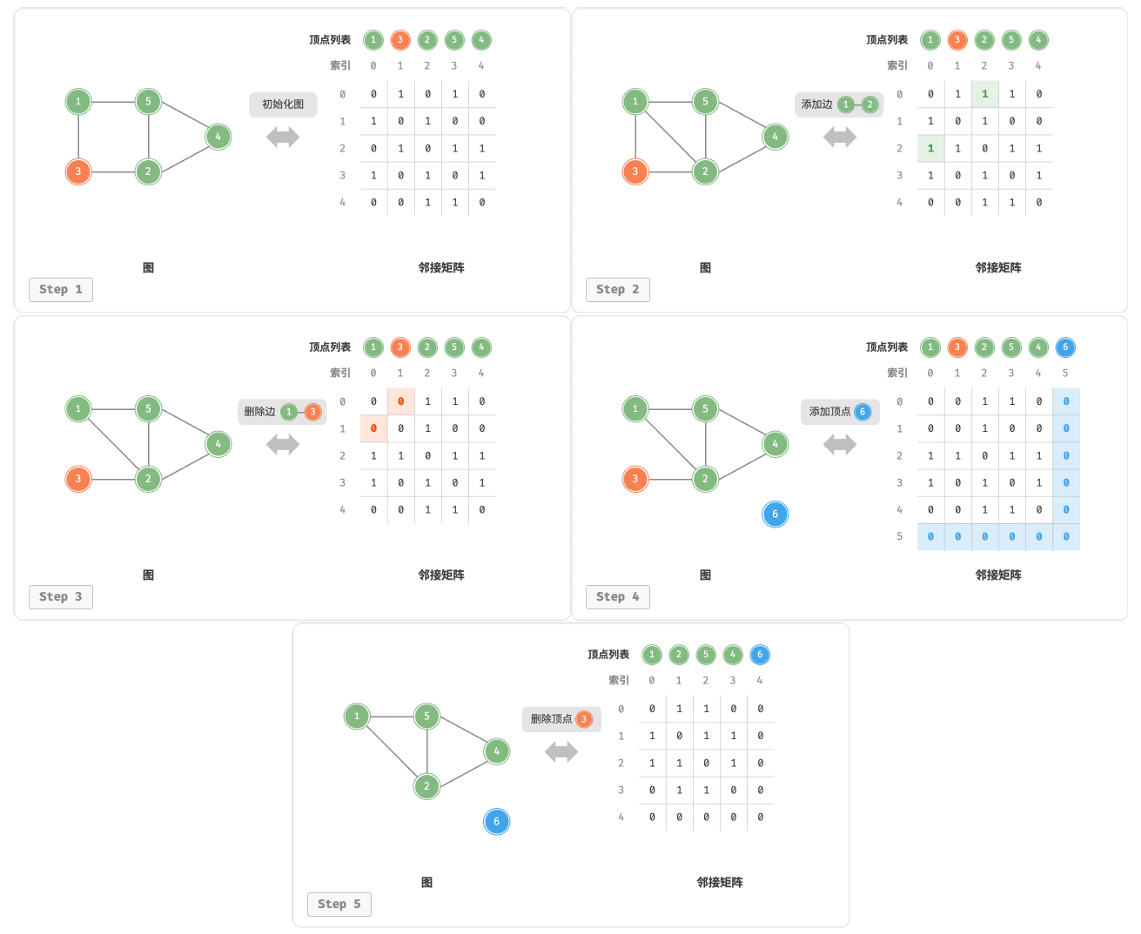image.png

我们的具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class GraphMap{
    private:
        vector<int> vertices;           // 顶点列表
        vector<vector<int>> adjMat;     // 邻接矩阵
    
    public:
        GraphMap(const vector<int> &vertices, const vector<vector<int>> &edges){
            for(int val : vertices)
                addVertex(val);
            for(const vector<int> &edge : edges)
                addEdge(edge[0],edge[1]);
        }

        int size() const{
            return vertices.size();
        }

        void addVertex(int val){
            int n = size();
            vertices.push_back(val);
            // 向邻接矩阵中添加一行
            adjMat.emplace_back(vector<int>(n,0));
            for(vector<int> &row: adjMat)
                row.push_back(0);
        }

        void removeVertex(int index){
            if(index >= size())
                throw out_of_range("顶点不存在");
            vertices.erase(vertices.begin() + index);
            // 删除行
            adjMat.erase(adjMat.begin() + index);
            // 删除列
            for(vector<int> &row : adjMat)
                row.erase(row.begin() + index);
        }

        void addEdge(int i,int j){
            if(i<0 || i>=size() || j<0 || j>=size() || i==j)
                throw out_of_range("顶点不存在");
            adjMat[i][j] = 1;
            adjMat[j][i] = 1;
        }

        void removeEdge(int i,int j){
            if(i<0 || i>=size() || j<0 || j>=size() || i==j)
                throw out_of_range("顶点不存在");
            adjMat[i][j] = 0;
            adjMat[j][i] = 0;
        }
};

基于邻接表的实现

设无向图的顶点总数为n、边总数为m，我们需要完成以下操作：

  • 添加边：在顶点对应链表的末尾添加边就行了。但是要注意无向图要加两个方向的边
  • 删除边：在顶点管理的链表中查找并删除指定的边。无向图中删两个方向。
  • 添加顶点：在邻接表中添加一个链表，并将新增顶点作为链表头节点
  • 删除顶点：遍历整个邻接表，删除包含指定顶点的所有边
  • 初始化：在邻接表中创建n个顶点和2m条边
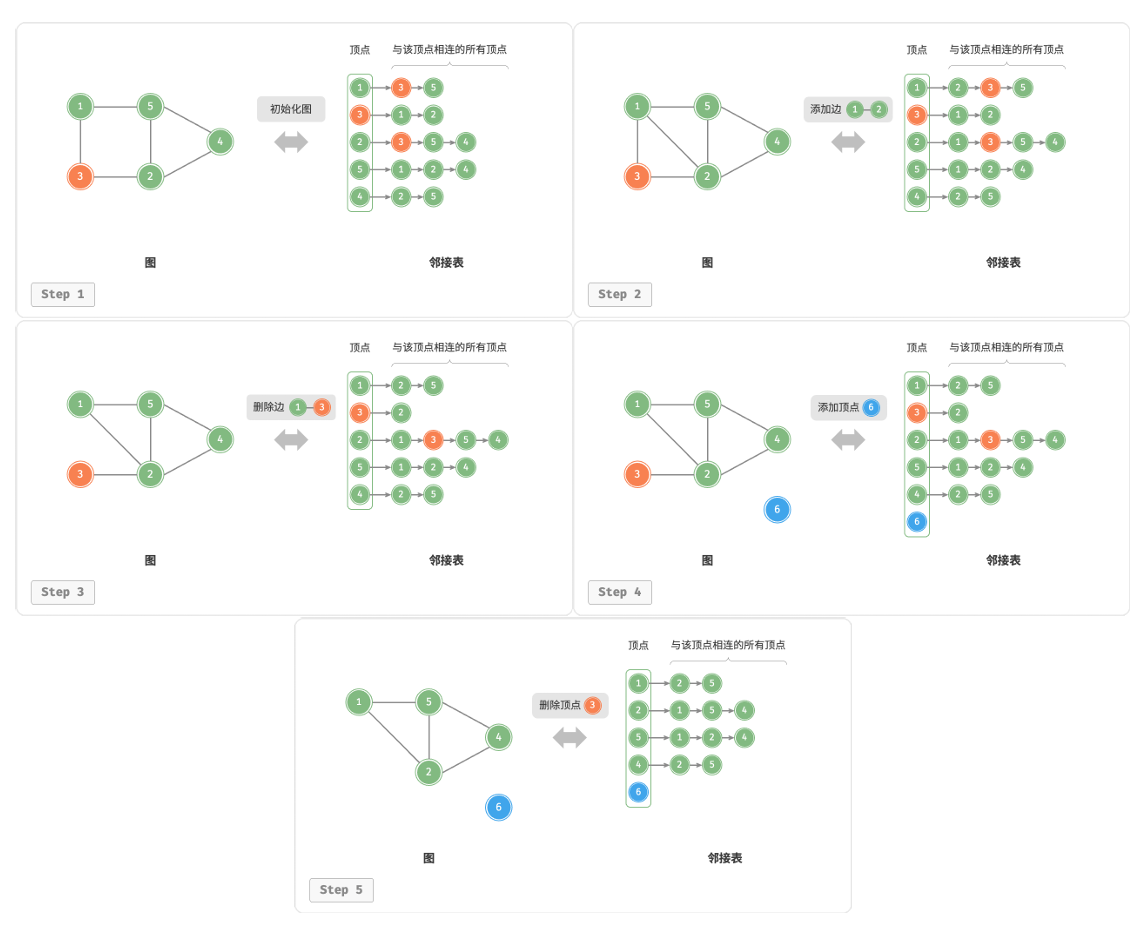image.png

以下是邻接表的代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class GraphList{
    private:
        unordered_map<Vertex* ,vector<Vertex*>> adjList;

        void remove(vector<Vertex*> &vec, Vertex* vet){
            for(int i=0;i<vec.size();i++){
                if(vec[i]==vet){
                    vec.erase(vec.begin()+i);
                    break;
                }
            }
        }

    public:
        GraphList(const vector<vector<Vertex*>> &edges){
            for(const vector<Vertex *> & edge: edges){
                addVertex(edge[0]);
                addVertex(edge[1]);
                addEdge(edge[0],edge[1]);
            }
        }

        int size(){
            return adjList.size();
        }

        void addVertex(Vertex* vet){
            if(adjList.count(vet))
                return;
            adjList[vet] = vector<Vertex*>();
        }

        void removeVertex(Vertex* vet){
            if(!adjList.count(vet))
                throw invalid_argument("不存在顶点");
            adjList.erase(vet);
            for(auto &adj : adjList)
                remove(adj.second,vet);
        }

        void addEdge(Vertex* vet1, Vertex* vet2){
            if(!adjList.count(vet1) || !adjList.count(vet2) || vet1==vet2)
                throw invalid_argument("不存在顶点");
            adjList[vet1].push_back(vet2);
            adjList[vet2].push_back(vet1);
        }

        void removeEdge(Vertex* vet1, Vertex* vet2){
            if(!adjList.count(vet1) || !adjList.count(vet2) || vet1==vet2)
                throw invalid_argument("不存在顶点");
            remove(adjList[vet1],vet2);
            remove(adjList[vet2],vet1);
        }
};

这里为了方便，我们使用动态数组代替了链表。用哈希表来表示邻接表结构。

同时需要注意在邻接表中我们使用Vertex类来表示顶点，也是为了方便。如果我们使用列表索引来区分不同德顶点的话，那么每当我们删除一个索引为i的顶点，就需要遍历整个邻接表，把所有索引大于i的顶点重新更新一遍，这样的话效率就很差。

图的遍历

树代表的是一对多的关系，图代表的是多对多的关系，所以我们可以将树视作图的一个特例。所以说树的遍历操作实际上也是图的遍历操作的一种特例。

和树类似的，我们有两种遍历方式实现对图的遍历操作：广度优先遍历和深度优先遍历

广度优先遍历

广度优先遍历是一种由近及远的遍历方式，从某个节点出发，始终优先访问距离最近的顶点，并一层层向外 扩张。以下图为例：

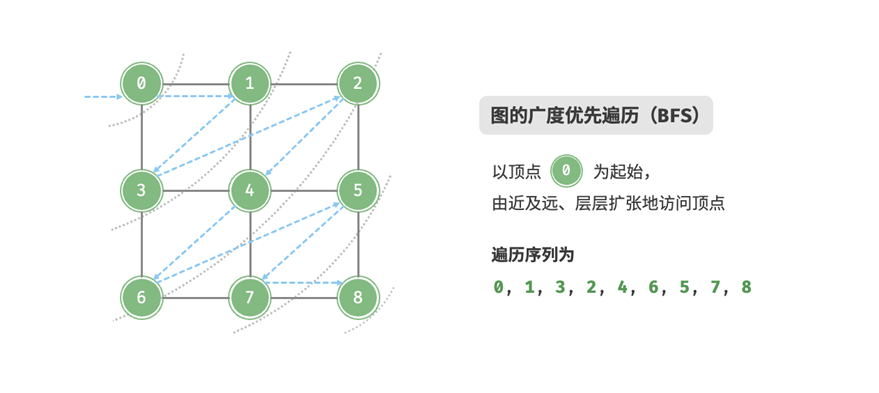image.png

从左上角顶点出发，首先遍历该顶点的所有邻接顶点，然后遍历下一个顶点的所有邻 接顶点，以此类推，直至所有顶点访问完毕。

算法实现

BFS通常需要一个辅助队列来实现，通过队列先进先出的性质，实现BFS由近及远的思路。我们的实现流程如下：

  • 将遍历起始顶点startVet加入队列中，开始循环
  • 在每次迭代中，弹出队首顶点并访问，将该顶点的所有邻接点加入到队列尾部
  • 循环上一步，知道队列为空

同时我们还需要一个哈希集合visited来记录哪些节点被访问，以防止重复遍历顶点。

我们的具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<Vertex*> graphBFS(GraphList &graph, Vertex* startVet){
    vector<Vertex*> res;				// 返回的顶点序列
    unordered_set<Vertex*> visited;		 // 哈希集合,用来记录被访问过的顶点	
    queue<Vertex*> que;					// 辅助队列	
    que.push(startVet);
    while(!que.empty()){
        Vertex* vet = que.front();
        que.pop();
        res.push_back(vet);
        for(auto adjVet : graph.adjList[vet]){
            if(visited.count(adjVet))
                continue;				// 跳过已访问的顶点
            que.push(adjVet);
            visited.emplace(adjVet);
        }
    }
    return res;
}

可以通过画图的方法帮助理解一下这个过程

深度优先遍历

深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。以下图为例

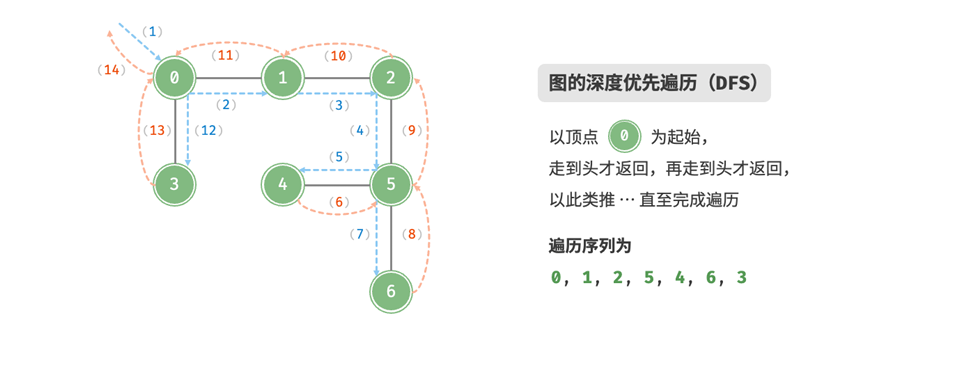image.png

算法实现

这种走到尽头并返回的样式，我们可以通过递归的方式实现。关键在于怎么设置边界条件，退出递归。我们的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void dfs(GraphList &graph, unordered_set<Vertex*> &visited,
         vector<Vertex*> &res, Vertex * vet){
    // 记录访问节点
    res.push_back(vet);
    // 标记已访问节点
    visited.emplace(vet);
	// 遍历所有邻接顶点
    for(Vertex* adjVet : graph.adjList[vet]){
        if(visited.count(adjVet))
            continue;
        // 递归访问邻接顶点
        dfs(graph,visited,res,adjVet);
    }
}

vector<Vertex*> graphDFS(GraphList &graph, Vertex* startVet){
    // 顶点遍历序列
    vector<Vertex*> res;
    // 以访问过的顶点
    unordered_set<Vertex*> visited;
    dfs(graph,visited,res,startVet);
    return res;
}

可以自己尝试手推一下这个过程，加深理解。