学一种新的数据结构——“堆”，但是貌似和底层原理中的堆并不一样。之前总是略有耳闻，但是一直都很少仔细去了解。

堆

堆是一种满足特定条件的完全二叉树，根据性质可以分为两种类型：

小顶堆：任意节点的值 <= 子节点的值
大顶堆：任意节点的值 >= 子节点的值

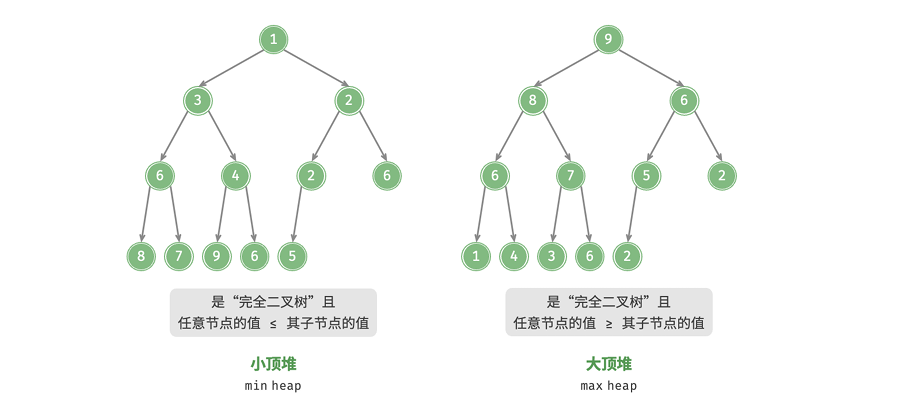
堆作为完全二叉树的一个特例，有以下规则：

最底层的节点靠左排列，其他层被节点填满。
二叉树的根节点被称为堆顶，二叉树底层靠右的节点称为堆底
对于大(小)顶堆，堆顶元素的值是最大(小)的

堆的常用操作

有一种抽象的数据结构——优先队列，定义为具有优先级排序的队列。通常我们会使用堆来实现优先队列，大顶堆就相当于元素按大到小的顺序出队的优先队列。这里我们将其视作等价的数据结构。

这里我们先通过优先队列来认识一下堆的一些操作：

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main(){
    priority_queue<int, vector<int>, greater<int>> minheap;
    priority_queue<int, vector<int>, less<int>> maxheap;

    maxheap.push(1);
    maxheap.push(5);
    maxheap.push(4);
    maxheap.push(2);
    maxheap.push(2);
    maxheap.push(3);

    cout << "The size is " << maxheap.size() << endl;
    int top = maxheap.top();
    cout << "The top is " << top << endl;

    bool isEmpty = maxheap.empty();

    return 0;
}

常用的可以总结为以下几类：

堆的实现

现在我们尝试从底层实现一个堆，这里我们用大顶堆演示，小顶堆只需要将所有的大小逻辑判断反转即可。

堆的存储和表示

堆是一种完全二叉树，我们之前提到过完全二叉树十分适合用数组来进行存储，所以这里我们的底层实现选择用数组，和之前的实现一样。我们使用索引的映射公式来代替节点指针：

int left(int i){
    return 2*i+1;
}

int right(int i){
    return 2*i+2;
}

int parent(int i){
    return (i-1)/2;
}

访问堆顶元素

堆顶元素就是二叉树的根节点，也就是我们数组的首元素：

class Heap{
    public:
		...
        int peek(){
            return heap[0];
        }
		...
    private:
        vector<int> heap;
};

元素入堆

给定val，我们将其添加到堆底。但是此时插入的值可能会破坏当前到根节点的路径，导致堆的成立条件被破坏。所以我们需要遍历修复从插入节点到根节点路径上的所有节点，这个过程我们称之为堆化

从入堆节点开始，我们从底执行堆化。我们依次比较当前节点和父节点的大小，如果插入节点更大就讲他们交换，知道修复所有的节点关系。

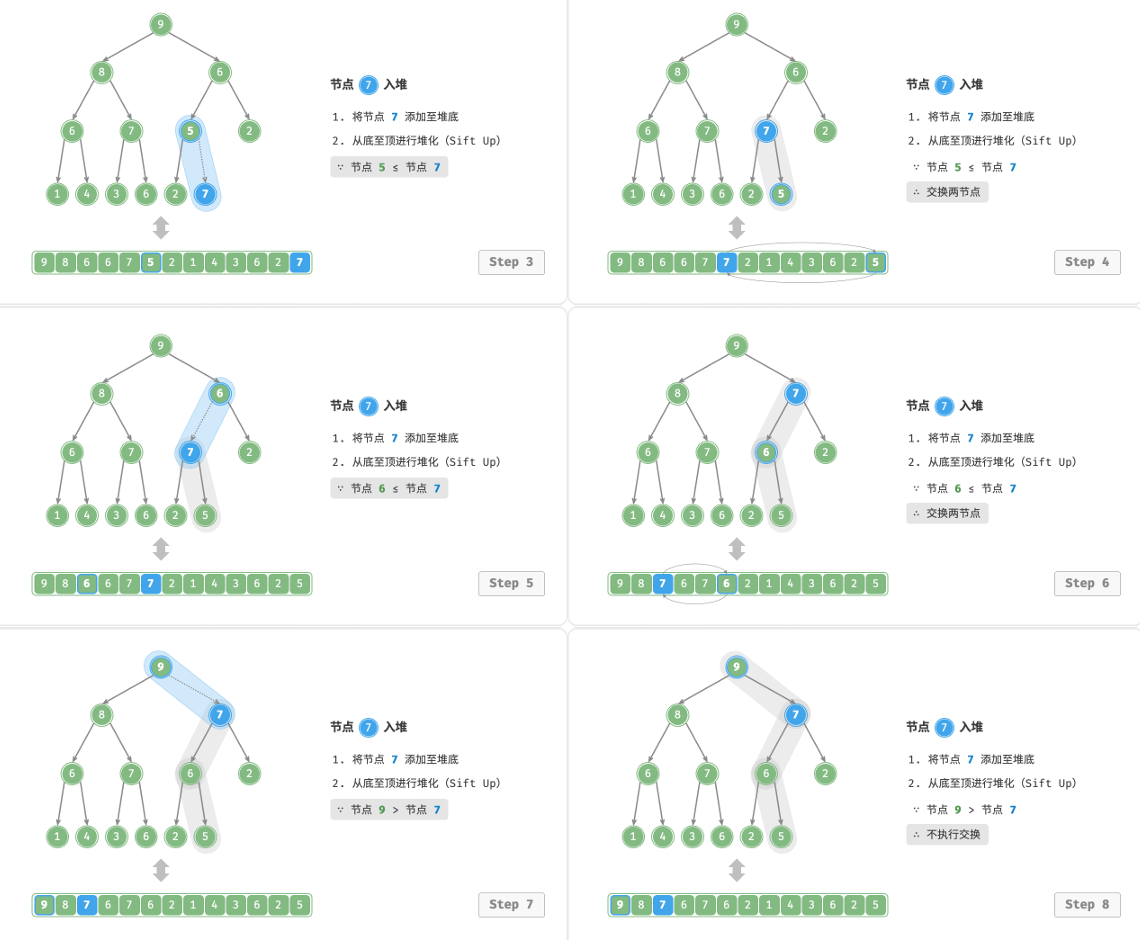
我们可以通过以下方式实现这个过程：

      void push(int i){
          heap.push_back(i);
          // 从堆底开始堆化
          siftUp(heap.size()-1);
      }
	
// 堆化
      void siftUp(int i){
          while(true){
              int p = parent(i);
              if(p<0 || heap[i] <= heap[p])
                  break;

              swap(heap[i],heap[p]);
              // 向上堆化
              i=p;
          }
      }

堆顶元素出栈

堆顶元素是二叉树的根节点，如果我们直接从数组中删除首元素，那么会破坏整个树的树状结构，这导致后续的堆化难以修复。所以我们采取以下步骤将堆顶元素出栈：

交换堆顶元素（根节点）和堆底元素（最右元素）
交换完成之后，我们将堆底删除
从根节点开始自顶向底执行堆化

自顶向下的堆化和自底向上的堆化逻辑相反，我们将当前节点和较大的子节点进行比较，然后进行交换，直到没有子节点或者无需再交换了：

出堆的实现方式如下：

void pop(int i){
    if(heap.empty())
        throw out_of_range("堆为空");
    swap(heap[i], heap[heap.size()-1]);
    heap.pop_back();
    siftDown(0);
}

void siftDown(int i){
    while(true){
        // ma为较大的节点
        int l=left(i), r=right(i), ma = i;
        if(l < heap.size() && heap[i] < heap[l])
            ma = l;
        if(r < heap.size() && heap[i] < heap[r])
            ma = r;
        // l,r越界或者i已经是最大节点 则退出堆化
        if(ma==i)
            break;
        swap(heap[i],heap[ma]);
        i = ma;
    }
}

建堆操作

我们希望能直接根据一个列表中的所有元素来构建一个堆。我们有两种可行的方案：

创建一个空堆，然后遍历列表，对每一个元素都进行入堆操作。但是对于n个元素执行复杂度为O(logn)的入堆操作，时间复杂度会增长到O(nlogn)
另一个方法就是，将列表中的元素添加到完全二叉树中，尽管现在的堆的性质并没有被满足。接下来我们倒序遍历堆，并对每个非叶节点进行一次自顶向下的堆化。这样每当我们堆化一个节点之后，都会以该节点为根节点形成一个子堆。

这里我们着重分析一下第二种方法。我们可以通过以下方法实现：

Heap(vector<int> vec){
    heap = vec;
    // 倒序遍历的第一个非叶节点 就是最后一个叶节点的父节点
    for(int i=parent(heap.size()-1); i>=0; i--)
        siftDown(i);
}

这个方法下的复杂度被优化到了O(n)，更加的便捷。

Top-k问题

所谓top-k问题，就是给定一个长度为n的无序数组nums，请返回数组中最大的k个元素。

对于这个问题我们有很多种解决方案：

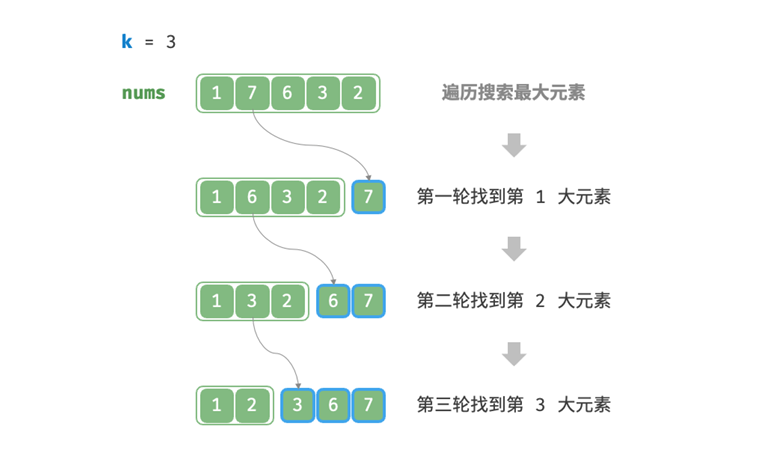
遍历选择

我们可以像这样对一个长度为n的序列进行k次遍历，每轮遍历都提取出当前序列中的最大的数据。时间复杂度为O(nk)。当k接近n时，时间复杂度增长到O(n^2)

排序

先对数组nums进行排序，然后再返回最右边的k个数据。这个方法主要取决于对数组排序的时间复杂度，对于std::sort，这个方法的复杂度是O(nlogn)

堆

我们可以基于堆更加高效的完成这个任务，我们遵循以下步骤实现：

初始化一个小顶堆，此时其堆顶元素最小。
然后将数组的前k个元素依次入堆
从第k+1个元素开始，如果当前元素大于堆顶元素，我们就将堆顶出堆，并将当前元素入堆。
遍历完成之后，堆中保存的就是最大的k个元素。

我们可以写出以下代码：

priority_queue<int, vector<int>, greater<int>> topHeap(vector<int> nums, int k){
    priority_queue<int, vector<int>, greater<int>> heap;
    for(int i=0;i<k;i++)
        heap.push(nums[i]);
    for(int i=k;i<nums.size();i++){
        if(heap.top() < nums[i]){
            heap.pop();
            heap.push(nums[i]);
        }
    }
    return heap;
}

总共进行了n轮入堆和出堆，由于堆大小是固定的k，所以我们只需要维护k个元素，所以实际上我们的计算复杂度只有O(nlogk)，在k较小时，我们的时间复杂度约等于O(n)

由此可以看到通过堆的思路，对解决TopK问题的显著提升。尤其是对于这种方法，适用于动态数据流的使用场景。在不断加入数据时，我们可以持续维护堆内的元素，从而实现最大的𝑘个元素的动态更新。

Ylin's Blog

98:堆

堆