Ylin's Blog
0%

97:平衡树

发表于 更新于 分类于 ，
本文字数： 1.4k 阅读时长 ≈ 5 分钟

书接上回，接着研究一下AVL树。

AVL树

在二叉搜索树中，我们可以知道，在多次的插入和删除之后，二叉树的左右可能会失去平衡，从而导致退化成链表，在这样的情况下我们的算法的效率会从O(logn)退化到O(n)：

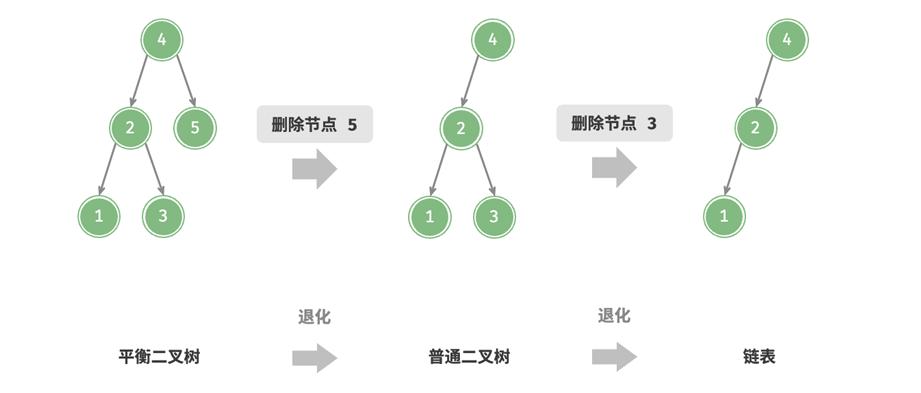image.png
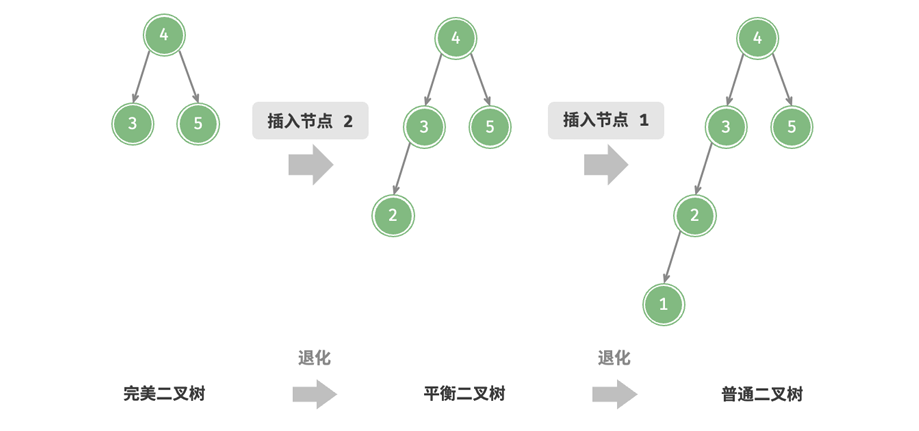image.png

但是我们接下来将要提到的AVL树，将解决这些问题

AVL树的常见术语

AVL树本质是二叉搜索树和二叉平衡树的结合，所以同时满足这两种树的性质：

  1. 节点高度

“节点高度”是指从该节点到它的最远叶节点的距离，即所经过的“边”的数量。这里我们让叶子节点的高度为0，把空节点的高度设置为-1。我们将根据这些性质来编写我们的数据结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
struct TreeNode{
    int val{};
    int height = 0;
    TreeNode* left{};
    TreeNode* right{};
    TreeNode() = default;
    explicit TreeNode(int x): val(x) {} 
};

// 获取高度
int height(TreeNode* node){
    return node == nullptr ? -1 : node->height;
}

// 更新节点高度
void updateHeight(TreeNode* node){
    // 当前节点的高度 = 最高子树高度 + 1
    node->height = max(height(node->left),height(node->right)) + 1;
}
  1. 节点的平衡因子

节点的平衡因子定义为节点左子树的高度减去右子树的高度，同时规定空节点的平衡因子为0。对于AVL树，我们要求树中任意节点的平衡因子-1<=f<=1，否则这个树就进入了失衡状态。我们可以写出以下函数：

1
2
3
int balance(TreeNode* node){
    return node == nullptr ? 0 : height(node->left) - height(node->right);
}

AVL树的旋转

AVL树的精髓就在于旋转操作，当我们的树中存在失衡节点时，我们可以通过“旋转”操作，在不影响中序遍历序列的前提下，使失衡的节点重新回到平衡的状态。

我们将|平衡因子| > 1的节点称为失衡节点，根据不同的失衡情况，我们有四种旋转操作：

右旋

image.png

结合这张图来看，从底至顶看，二叉树中首个失衡节点是“节点3”。我们关注以该失衡 节点为根节点的子树，将该节点记为 node ，其左子节点记为 child ，执行“右旋”操作。完成右旋后，子树 恢复平衡，并且仍然保持二叉搜索树的性质。

但是对于，当节点child有右节点（记作grand_child）的情况下，我们需在右旋中添加一步：将grand_child设置为node的左子节点。

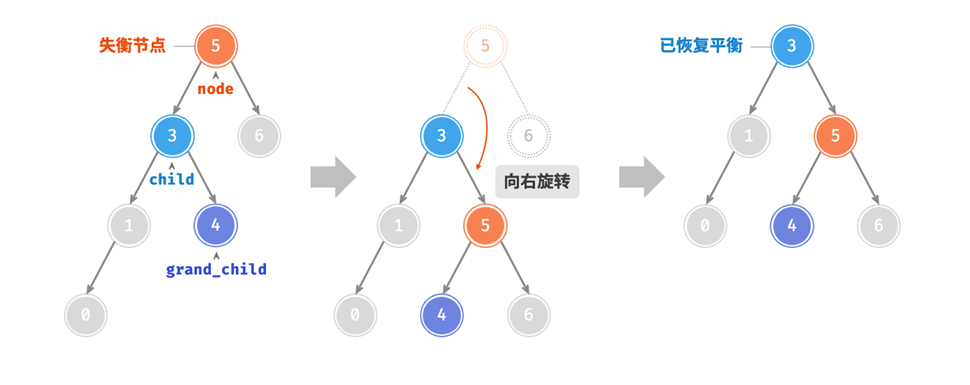image.png

我们可以通过修改节点指针的方法来实现：

1
2
3
4
5
6
7
8
9
10
11
TreeNode* rightRotate(TreeNode* node){
    TreeNode* child = node->left;
    TreeNode* grandChild = child->right;
    child->right = node;
    // 当grandChild为null时无影响
    node->left = grandChild;
    updateHeight(child);
    updateHeight(node);
    // 右旋后child作为左子树的根节点
    return child;
}

左旋

左旋作为右旋的镜像版本，对应右节点失衡的情况，同样是下面的两种情况：

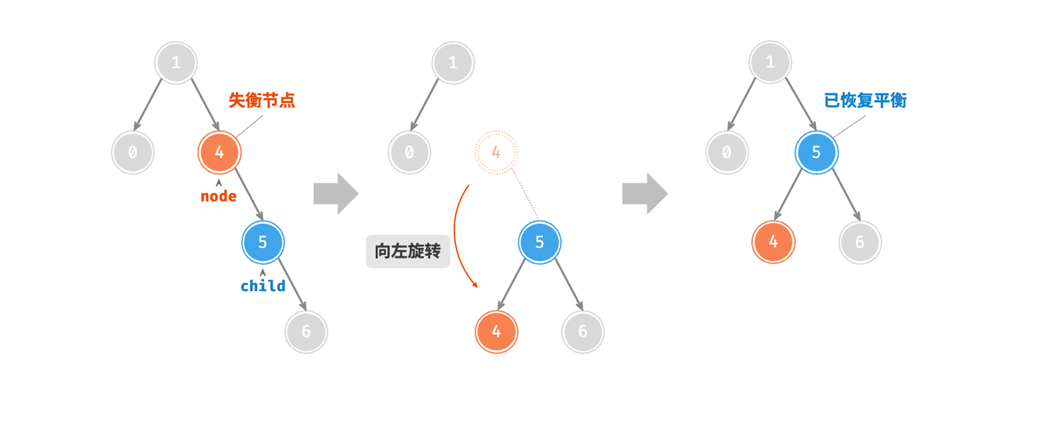image.png
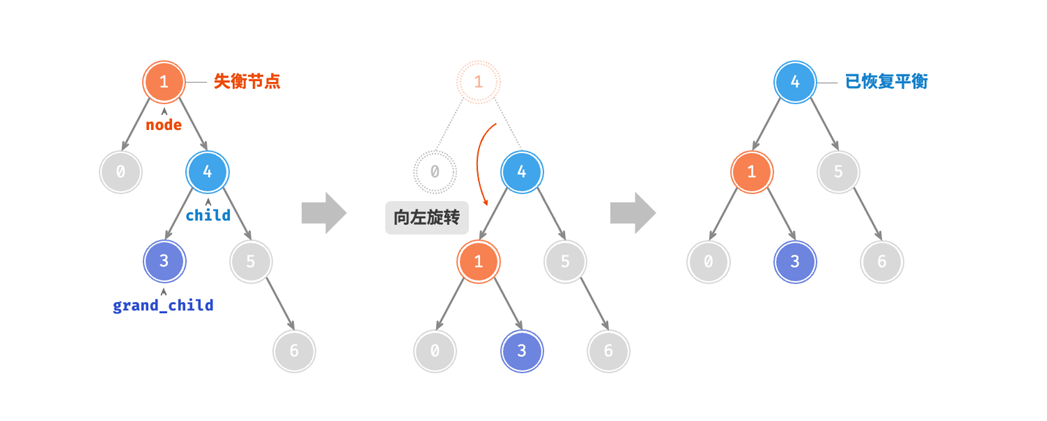image.png

我们可以写出：

1
2
3
4
5
6
7
8
9
TreeNode* leftRotate(TreeNode* node){
    TreeNode* child = node->right;
    TreeNode* grandChild = child->left;
    child->left = node;
    node->right = grandChild;
    updateHeight(child);
    updateHeight(node);
    return child;
}

先左旋后右旋

对于下面这种情况，我们需要先对child进行左旋，再对node进行右旋：

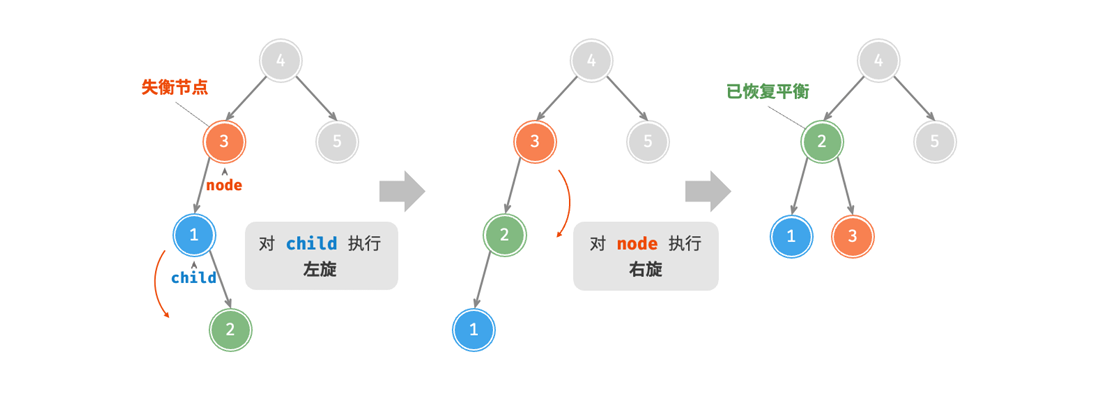image.png

先右旋后左旋

这种情况依旧是上一种情况的镜像对称情况：

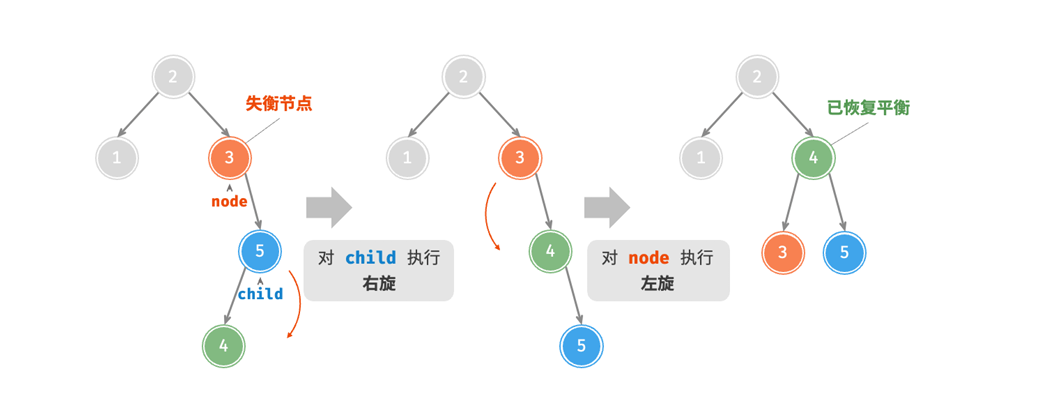image.png

旋转的选择

讲完了四种旋转的操作，现在我们需要分析，在什么情况下需要对我们的树进行哪些操作了，这里的话我推荐看一个视频：平衡二叉树(AVL树)_哔哩哔哩_bilibili

我们的步骤总结如下：

  • 先检查失衡节点的子节点child的平衡因子，大于0则需要进行右旋操作，小于0则需要进行左旋操作。
  • 然后检查失衡节点node的平衡因子，大于1则需要进行右旋操作，小于1则需要左旋操作。
  • 最后比较对子节点chlid和失衡节点node的需要进行的操作，如果相同则合并，不同则先操作子节点后操作失衡节点。

我们也可以用一张表来进行这个判断：

image.png

现在我们可以写出AVL树的平衡函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
TreeNode* rotate(TreeNode* node){
    int _balanceFactor = balance(node);
    TreeNode* child = node->left;
    if(_balanceFactor > 1){
        // 右旋
        if(balance(child)<-1)
            // 先左旋
            child = leftRotate(child);
        return rightRotate(node);
    }else if(_balanceFactor < -1){
        // 左旋
        if(balance(child)>1)
            // 先右旋
            child = rightRotate(child);
        return leftRotate(node);
    }else{
        // 平衡
        return node;
    }
}

AVL树的常用操作

  1. 插入节点

AVL树的节点插入操作和二叉搜索树一样，只不过在AVL树插入节点之后，从这个节点到根节点的路径上可能会出现一系列的失衡节点。所以我们需要从这个节点开始，自底向上的执行平衡操作，知道所有的失衡节点都恢复平衡。我们的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
TreeNode* _insert(TreeNode* node, int num){
    if(node==nullptr)
        return new TreeNode(num);
    if(num < node->val)
        node->left = _insert(node->left,num);
    else if(num > node->val)
        node->right = _insert(node->right,num);
    else 
        return node;
    
    updateHeight(node);
    return rotate(node);
}
  1. 删除操作

删除也是差不多，需要在删除的基础之上，从底部到顶部进行平衡操作，确保所有的失衡点都恢复平衡：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
TreeNode* _remove(TreeNode* node, int num){
    if(node==nullptr)
        return nullptr;
    if(num < node->val)
        node->left = _remove(node->left,num);
    else if(num > node->val)
        node->right =_remove(node->right,num);
    else{
        if(node->left==nullptr||node->right==nullptr){
            TreeNode* child = node->left==nullptr ? node->right : node->left;
            delete node;
            return child;
        }else{
            TreeNode* tmp = node->right;
            while(tmp->left !=nullptr)
                tmp = tmp->left;
            int val = tmp->val;
            node->right = _remove(node->right,tmp->val);
            node->val = val;
        }
    }
    updateHeight(node);
    return rotate(node);
}
  1. 查找操作

和二叉搜索树一样，没有变化