Ylin's Blog
0%

95:树

发表于 更新于 分类于 ，
本文字数： 2.6k 阅读时长 ≈ 10 分钟

打算系统性的学一下数据结构与算法，这个就相当于笔记做一下记录了。 # 树

二叉树

二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用。我们可以用以下数据结构表示：

1
2
3
4
5
6
struct TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x): val(x), left(nullptr), right(nullptr){}
};

这里每个节点都有两个引用，分别为左右子节点，中间的节点为这两个节点的父节点。左右子树的概念也可以类推。在二叉树中，除叶节点外，其他所有节点都包含子节点和非空子树。

二叉树常用的术语

二叉树中的性质较为复杂，所以我们需要记住许多相关的术语：

  • 根节点：位于二叉树顶层的节点，没有父节点。
  • 叶节点：没有子节点的节点，其两个指针均指向 None
  • 边：连接两个节点的线段，即节点引用（指针）
  • 节点所在的层：从顶至底递增，根节点所在层为1。
  • 节点的度：节点的子节点的数量。在二叉树中，度的取值范围是0、1、2。
  • 二叉树的高度：从根节点到最远叶节点所经过的边的数量
  • 节点的深度：从根节点到该节点所经过的边的数量。
  • 节点的高度：从距离该节点最远的叶节点到该节点所经过的边的数量。
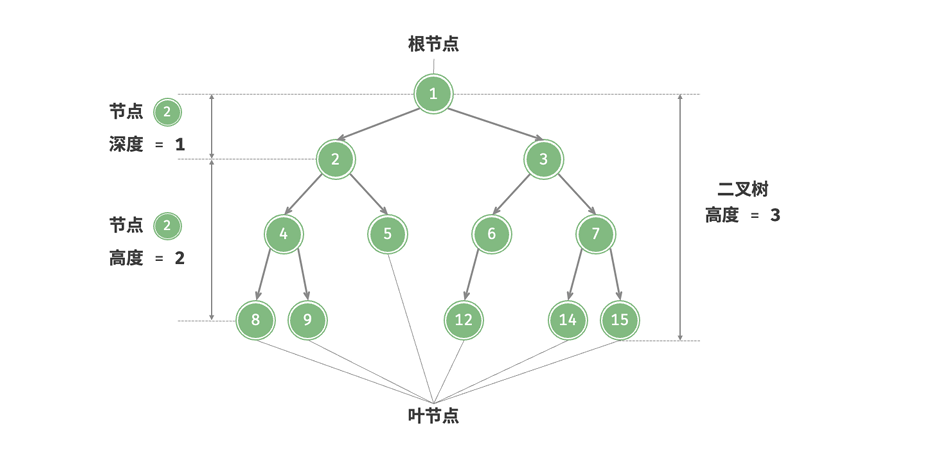image.png

二叉树的基本操作

  1. 初始化二叉树

​ 初始化节点，并构造引用：

1
2
3
4
5
6
7
8
9
10
11
12
int main(){
    TreeNode* n1 = new TreeNode(1);
    TreeNode* n2 = new TreeNode(2);
    TreeNode* n3 = new TreeNode(3);
    TreeNode* n4 = new TreeNode(4);
    TreeNode* n5 = new TreeNode(5);

    n1->left = n2;
    n1->right = n3;
    n2->left = n4;
    n2->right = n5;
}
  1. 插入与删除节点

​ 二叉树中的插入与删除节点可以通过修改指针实现，效果见下图：

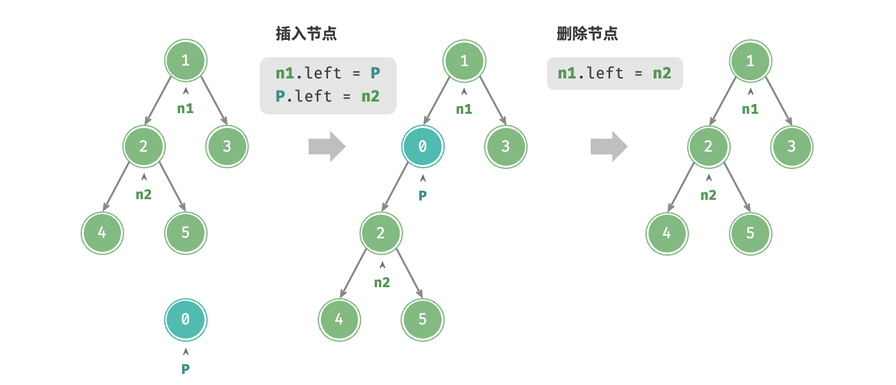image.png

二叉树的类型

完美二叉树

完美二叉树的所有层的节点都被完全填满。且在完美二叉树中，叶节点的度为0，其余所有节点的度都为2；若树的高度为ℎ，则节点总数为2ℎ+1−1，呈现标准的指数级关系：

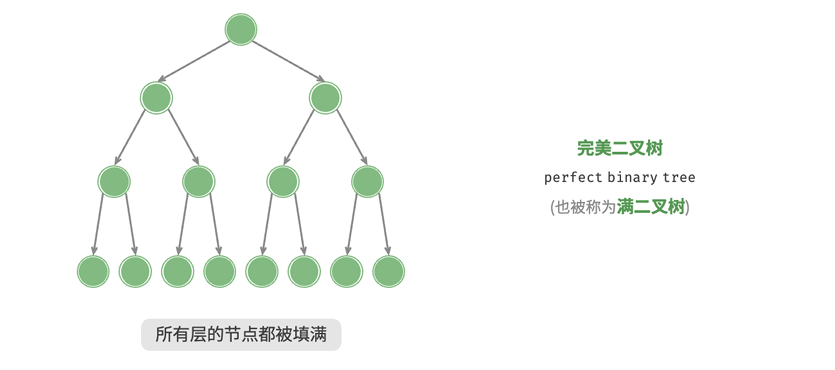image.png

关于完美二叉树，我们需要注意到它的几个性质：

  • 第i层的节点数量： 2i − 1
  • 高度为h的树的叶节点数量：2h
  • 高度为h的树的节点总数： 2h + 1 − 1
  • 节点总数为n的树的高度：log2(n + 1) − 1

完全二叉树

完全二叉树只有最底层的节点未被填满，且最底层的节点尽量靠左边。

注：完美二叉树是一种特殊的完全二叉树

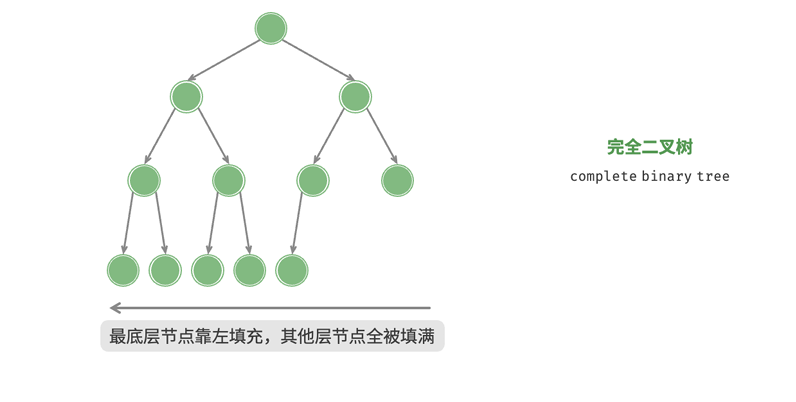image.png

完满二叉树

完满二叉树除了叶子节点之外，其余所有节点都有两个子节点：

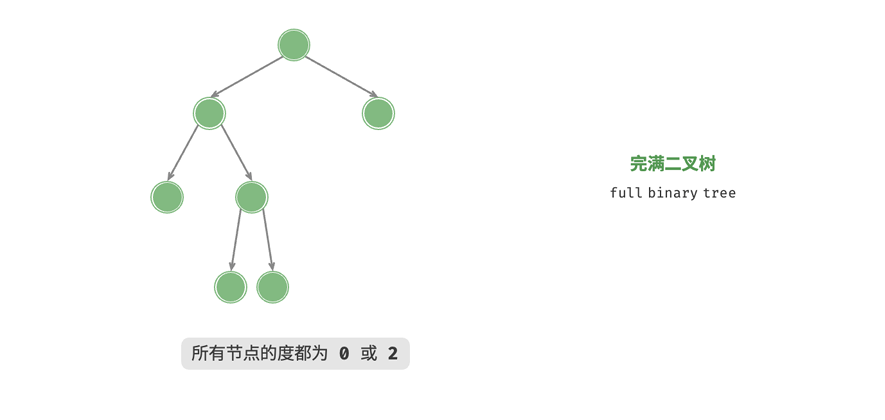image.png

平衡二叉树

平衡二叉树中的任意节点的左子树和右子树的高度之差的绝对值不超过1，|左子树高度-右子树高度|<=1

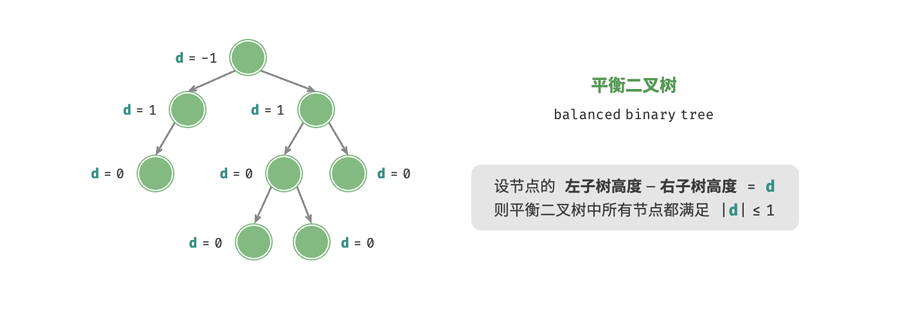image.png

二叉树遍历

常见的二叉树遍历有：层序遍历、前序遍历、中序遍历和后序遍历

层序遍历

层序遍历是从顶部到底部逐层遍历二叉树，并在每一层按照从左到右的顺序访问节点。这种遍历方式本质上属于广度优先遍历，我们也称之为广度优先搜索：

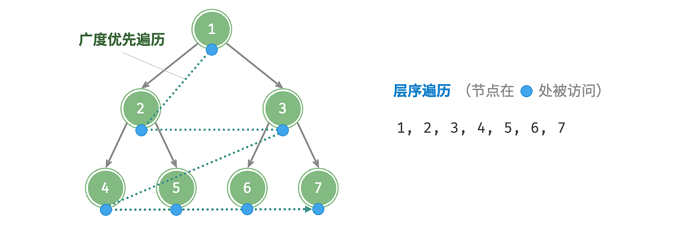image.png

其代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<int> BFS(TreeNode* root){
    queue<TreeNode*> q;		// 用于存放遍历序列
    q.push(root);
    vector<int> vec;
    while(!q.empty()){
        TreeNode* node = q.front();
        q.pop();			// 将需要处理的节点出列
        vec.push_back(node->val);
        if(node->left!=nullptr)
            q.push(node->left);
        if(node->right!=nullptr)
            q.push(node->right);
    }
    return vec;
}

前中后序遍历

相应的这种遍历方式实际上是一种深度优先的遍历，我们称之为深度有限的搜索。这里我们有三种不同的遍历顺序，我们可以通过简单的递归来实现，具体实现如下。就不做过多的说明，因为很直观：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 前序
void preOrder(TreeNode* root){
    if(root==nullptr)
        return;
    cout << root->val << endl;
    preOrder(root->left);
    preOrder(root->right);
}
// 中序
void inOrder(TreeNode* root){
    if(root==nullptr)
        return;
    inOrder(root->left);
    cout << root->val << endl;
    inOrder(root->right);
}
// 后序
void pastOrder(TreeNode* root){
    if(root==nullptr)
        return;
    pastOrder(root->left);
    pastOrder(root->right);    
    cout << root->val << endl;
}

二叉树的数组表示

我们先前对二叉树的实现是通过链表进行实现的，节点之间则通过指针连接。但是实际上我们也可以通过数组实现二叉树的结构。

表示完美二叉树

对于一颗完美二叉树，我们可以将所有的节点按照层序遍历的顺序存储一个数组中，则每个节点都对应唯一的数组索引，根据层序遍历的特性，我们也可以推导出父子节点之间的索引关系：

若某节点的索引为𝑖， 则该节点的左子节点索引为2𝑖+1，右子节点索引为2𝑖+2

这里的映射关系就相当于先前的指针，我们只需要知道当前的索引，就能找到其对应的左右节点

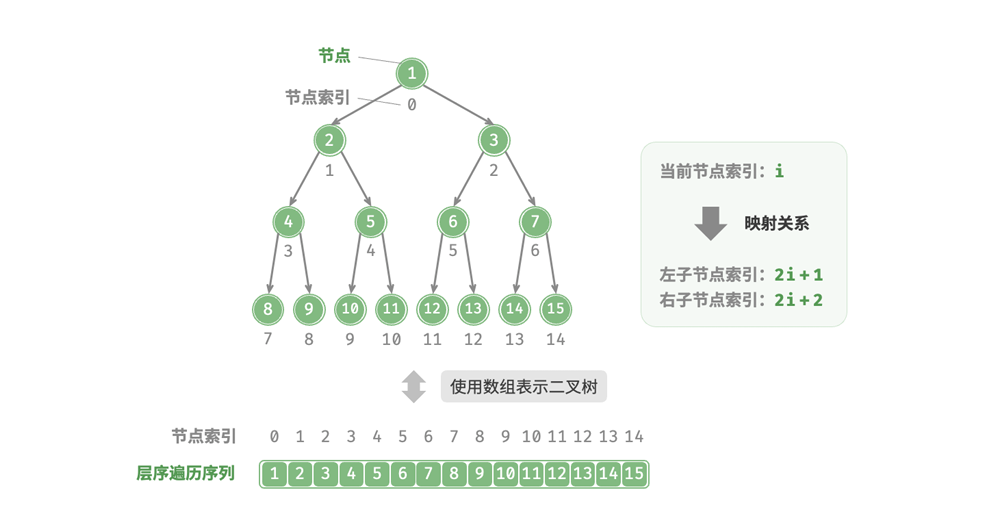image.png

表示任意二叉树

完美二叉树是一个特例，在实际情况中，我们的二叉树中间层有很多None，如果层序遍历不包含这些None，那么我们就无法根据一个数组来还原二叉树的形态：

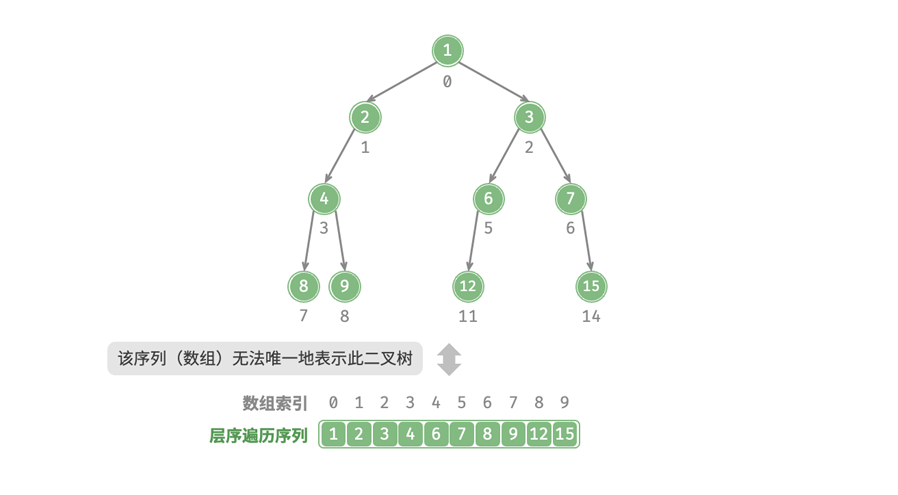image.png

所以我们尝试在层序遍历的序列中显式的写出所有的None:

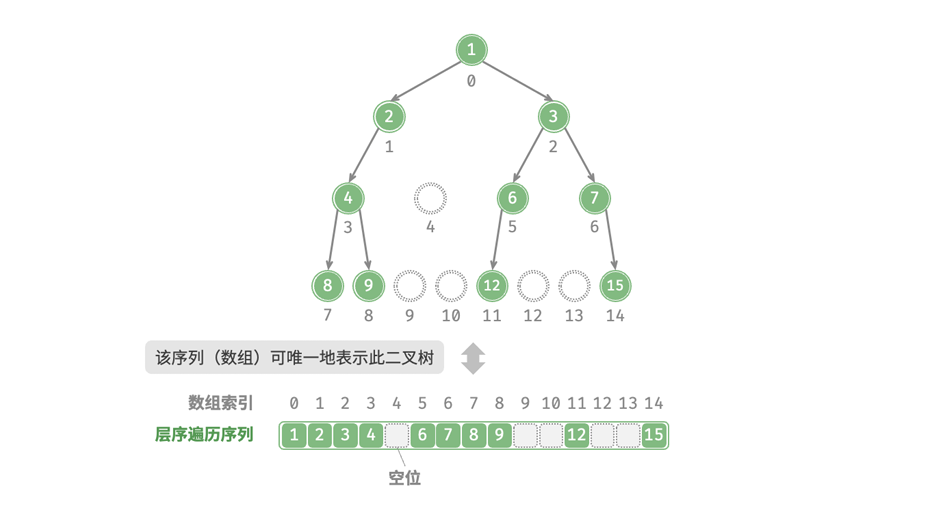image.png

就可以清晰的表示一个二叉树的结构。当然需要注意的是，完全二叉树十分适合用数组来表示，我们知道其None只会出现在最底层的右边，一定出现在层序遍历序列的末尾。这意味着当我们对完全二叉树进行存储时，我们可以忽略所有的None

二叉树的数组实现

现在我们尝试用数组实现二叉树的结构，我们需要支持以下操作：

  • 给定某节点，获取其值、左右子节点、父节点
  • 获取前序、中序、后序遍历、层序遍历序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <vector>
#include <iostream>

using namespace std;

class ArrayBinaryTree{
public:
    ArrayBinaryTree(vector<int> arr){
        tree = arr;
    }

    int size(){
        return tree.size();
    }

    int val(int i){
        if(i<0 || i>=size())
            return -1;
        return tree[i];
    }

    int left(int i){
        return 2*i+1;
    }

    int right(int i){
        return 2*i+2;
    }

    int parent(int i){
        return (i-1)/2;
    }

    vector<int> BFS(){
        vector<int> res;
        for(int i=0;i<size();i++)
            if(val(i)!=-1)
                res.push_back(val(i));
        return res;
    }

    void preOrder(int index){
        if(val(index)==-1)
            return;
        cout << val(index) << endl;
        preOrder(left(index));
        preOrder(right(index));
    }

    void inOrder(int index){
        if(val(index)==-1)
            return;
        inOrder(left(index));
        cout << val(index) << endl;
        inOrder(right(index));
    }

    void pastOrder(int index){
        if(val(index)==-1)
            return;
        pastOrder(left(index));
        pastOrder(right(index));
        cout << val(index) << endl;
    }
    
private:
    vector<int> tree;
};

二叉搜索树

如下图所示，二叉搜索树需要满足以下条件：

  • 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树所有节点的值
  • 任意节点的左右子树也时二叉搜索树，满足上一个条件
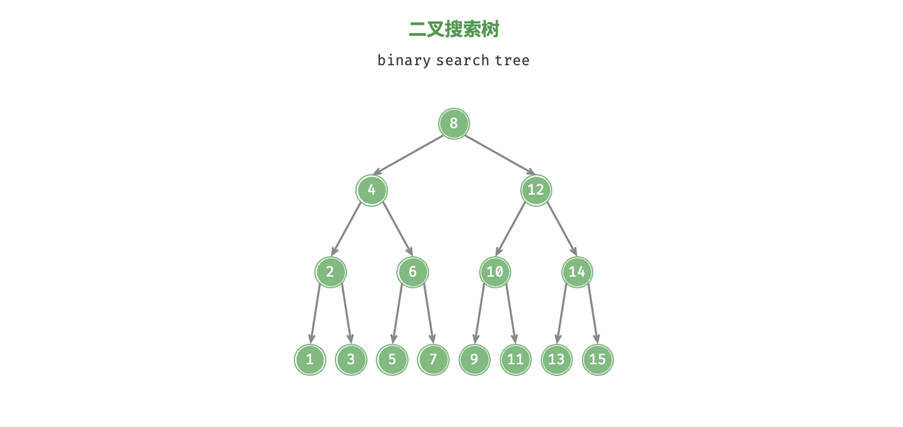image.png

二叉搜索树的操作

我们将二叉搜索树封装为一个类BinarySerchTree，并声明一个成员变量root，指向树的节点。

  1. 查找节点

给定一个目标节点值num，我们可以很快的根据二叉搜索树的性质来查找，我们可以声明一个节点cur，从二叉树的根节点root出发，循环比较值，知道找到对应的节点。

二叉搜索树的查找操作实际上和二分查找差不多，循环次数最多为树的高度：

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode* search(int num){
           TreeNode* cur = root;
           while(cur != nullptr){
               if(cur->val < num)
                   cur = cur->right;
               else if(cur->val > num)
                   cur = cur->left;
               else
                   break;
           }
           return cur;
       }
  1. 插入节点

给定一个等待插入的元素num，为了保持二叉树的性质，我们进行以下步骤：

  • 查找插入位置：和查找操作相似，从根节点出出发，直到越过叶节点时退出循环。
  • 在该位置插入节点：初始化节点num，将该节点置于none的位置。
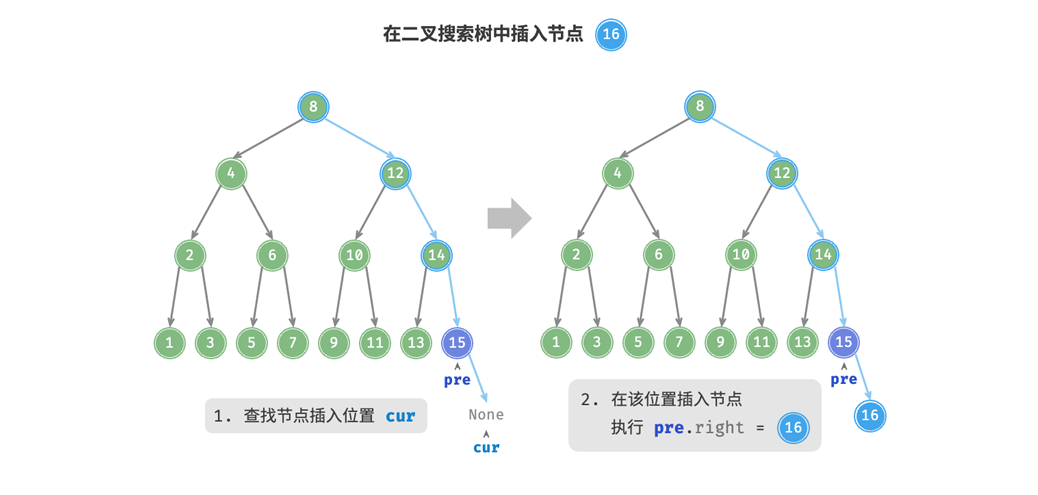image.png

在编写的过程中我们需要注意两点：

  • 如果插入的数值已经存在，那么则不插入。
  • 使用pre节点保存cur的上一个位置，以为我们指定插入位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void insert(int num){
           if(root == nullptr) return;
           TreeNode* cur = root;
           TreeNode* pre = nullptr;
           while(cur != nullptr){
               if(cur->val == num)
                   return;
               pre = cur;
               if(cur->val < num)
                   cur = cur->right;
               else
                   cur = cur->left;
           }
           TreeNode* node = new TreeNode(num);
           if(num > pre->val)
               pre->right = node;
           else
               pre->left = node;
       }
  1. 删除节点

在二叉树中查找到目标节点，并将其删除，和插入节点类似，我们需要保证在删除操作完成之后仍然保持着二叉树的性质。所以我们需要根据目标子节点的数量，分为0\1\2三种情况进行相应的处理。

对于度为0的情况，我们只需要简单的删除：

image.png

当度为1时，我们需要将待删除的节点替换成其子节点：

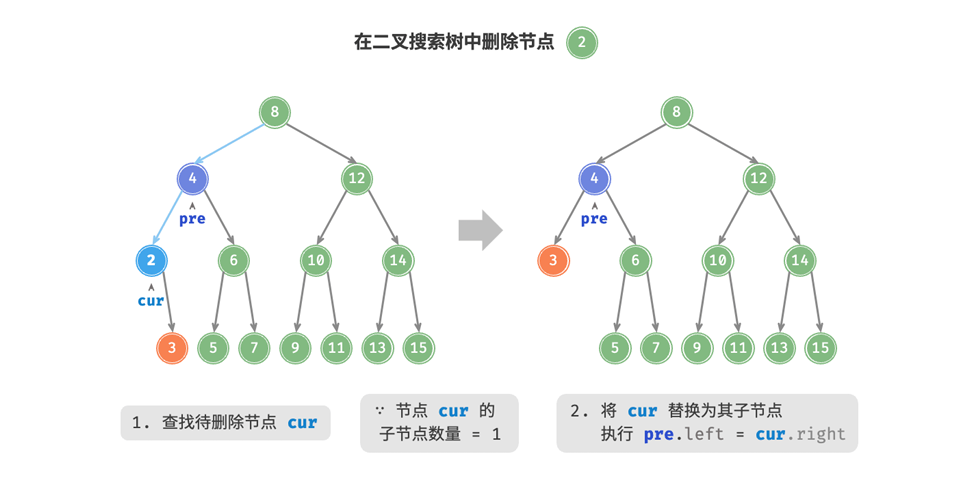image.png

对于度为2的节点，我们则需要谨慎处理。首先我们需要找到一个能替换它的节点（左子树的最大值或是右子树的最小值），并将其删除，覆盖待删除的节点：

  • 找到待删除节点在中序遍历序列中的下一个节点，记为tmp
  • 用tmp的值覆盖待删除节点的值，并在书中递归删除节点tmp
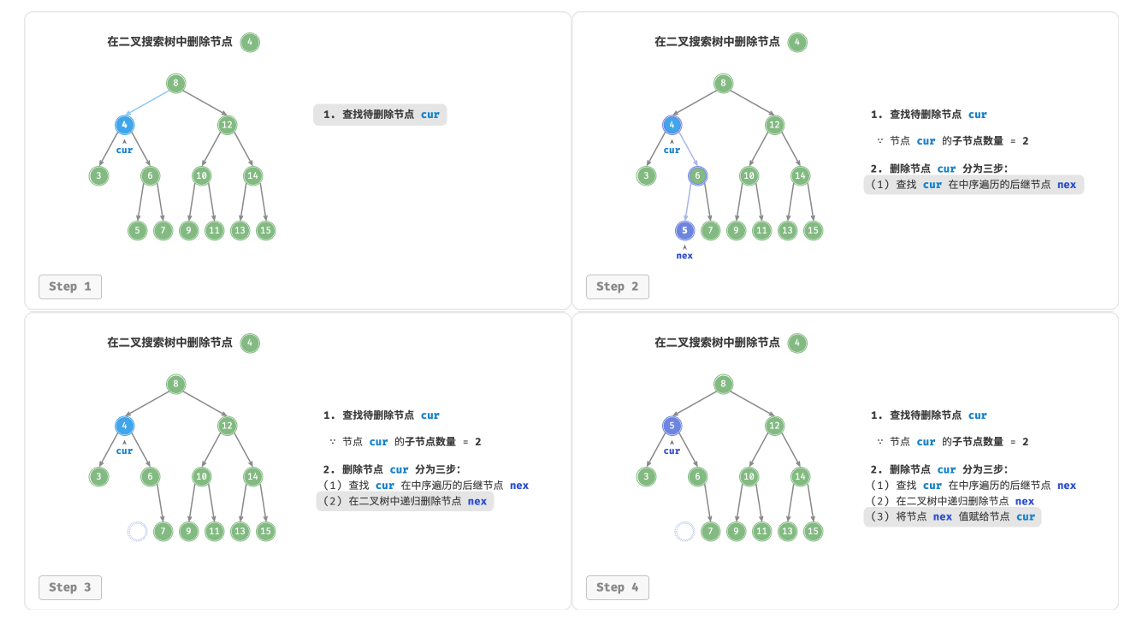image.png

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void remove(int num){
    if(root == nullptr) return;
    TreeNode* cur = root;
    TreeNode* pre = nullptr;
    while(cur != nullptr){
        if(cur->val == num)
            break;
        pre = cur;
        if(cur->val < num)
            cur = cur->right;
        else
            cur = cur->left;
    }
    if(cur == nullptr) return;
    // 度为0/1
    if(cur->left==nullptr || cur->right==nullptr){
        TreeNode* child = cur->left==nullptr?cur->right:cur->left;
        if(cur!=root){
            if(pre->left==cur)
                pre->left = child;
            else
                pre->right = child;
        }else{
            root = child;
        }
        delete cur;
    }else{
        TreeNode* tmp = cur->right;
        // 寻找后继节点
        while(tmp->left!=nullptr)
            tmp = tmp->left;
        // 递归删除后继节点
        remove(tmp->val);
        cur->val = tmp->val;
    }
}
  1. 中序遍历有序

由于搜索二叉树的性质，当我们对其进行中序遍历时，总是会优先遍历下一个最小节点，所以我们知道：搜索二叉树的中序遍历时升序的。所以我们可以直接得到搜索二叉树的有序数据。

AVL树

之后单独开一篇讲 感觉比较复杂