最近很流行这些,出于好奇,我也想知道这些技术背后的原理是什么。而且我感觉很多知识可能之后会用到,所以我打算浅浅的了解一下。最终的目标是实现一个手写数字识别的神经网络吧。试试看吧。
神经网络简介
基础构件:神经元
神经元是神经网络的基本单元。它接受输入,对数据进行计算从而产生一个输出。比如下面的一个二元输入神经元样例:
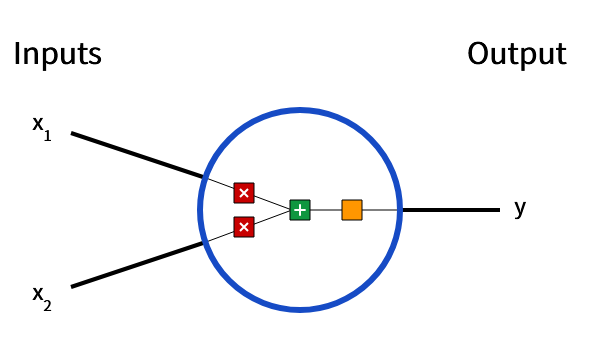 image.png
image.png
这个神经元进行了以下操作:
输入乘以权重w:
x1 –> x1 * w1 x2 –>
x2 * w2
加权输入与偏置b相加:
( x1 * w1) + (x2 * w2) +
b
最后将总和传递给激活函数:(其中f是激活函数)
y = f(x1 * w1 + x2 * w2 +
b)
对于任意输入的神经元,我们的输出是:
$$
y = f\left(\sum_{i=1}^{n} w_i x_i + b\right)
$$
对于激活函数f我们需要额外了解到,在不引入激活函数的情况下,我们的输出和下一个输入的结果之间总是线性的关系。我们使用激活函数则可以将无界的输入转换成良好的、可以预测形式的输出。这里我们使用的激活函数是sigmoid函数:
$$
\begin{aligned}
f(x)=\frac{1}{1+e^{-x}}
\end{aligned}
$$
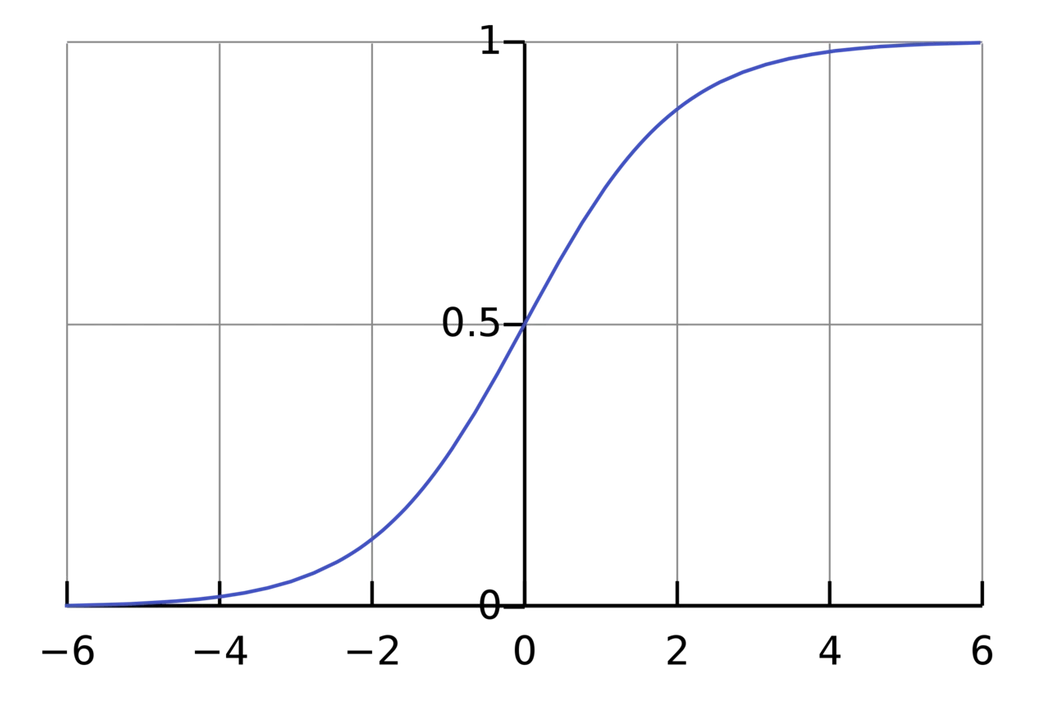 image.png
image.png
sigmoid函数只输出(0,1)范围内的数值,它将(−∞, +∞)的数值压缩到了(0,1).
简单的举例
假设我们现在有一个使用sigmoid激活函数的二元输入神经元,其w=[0,1] b=4
若我们想神经元输入x = [2,3],我们可以得到
1
2
3
| (w * x) + b = 0*2 + 1*3 + 4
= 7
y = f(w*x+b) = f(7) = 0.999
|
我们向前传递输入以获取输出,这个过程我们称之为前馈(feedforward)
神经元的代码实现
我们使用Python中的numpy来实现这个功能:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| import numpy as np
def sigmoid(x: float) -> float:
return 1/(1+np.exp(-x))
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0,1])
bias = 4
n = Neuron(weights,bias)
x = np.array([2,3])
print(n.feedforward(x))
|
可以看到我们的输出和我们的计算是吻合的
将神经元组合成神经网络
神经网络实际上是许多相互连接的神经元,一个简单的神经元长这样:
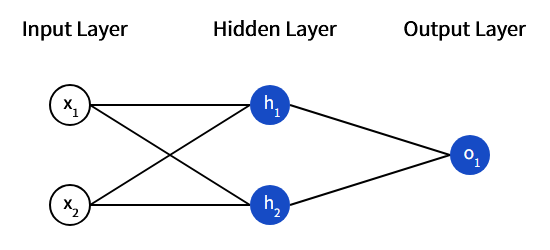 image.png
image.png
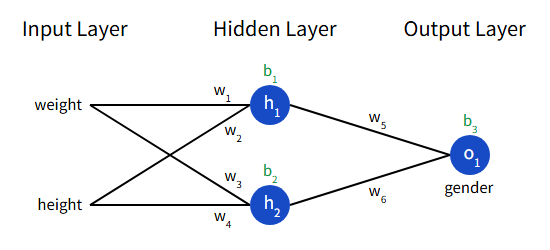
这个网络有两个输入组成的输入层,还有两个神经元(h1,h2)组成的隐藏层,以及一个神经元(o1)组成的输出层。其中隐藏层指的是位于输入层和输出层之间的任何层,可以有多个隐藏层。
简单的举例:前馈计算
我们使用上述的网络,令每个神经元都是使用sigmoid激活函数且w=[0,1] b=0,用h1 h2 o1来表示神经元的输出,则有:
1
2
3
4
5
6
7
| h1 = h2 = f(w*x+b)
=f((0*2)+(1*3)+0)
=f(3)
=0.9526
o1 = f(w*x+b)
= f(0.9526)
= 0.7216
|
此时我们的神经网络的前馈就是0.7216,整个过程简而言之就是,将输入信息通过网络中的神经元向前传递,最终得到输出信息,作为整个神经网络的前馈
神经网络的代码实现
现在我们为这个简单的神经网络实现前向传播
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class NeuralNetwork:
def __init__(self):
weights = np.array([0,1])
bias = 0
self.h1 = Neuron(weights,bias)
self.h2 = Neuron(weights,bias)
self.o1 = Neuron(weights,bias)
def feedforword(self,x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
out_o1 = self.o1.feedforward(np.array([out_h1,out_h2]))
return out_o1
network = NeuralNetwork()
x = np.array([2,3])
print(network.feedforword(x))
|
和我预期的答案是吻合的
训练神经网络
损失
训练神经网络意味着,有预测的答案和实际的答案。训练的过程就是让网络预测的结果贴合真实的答案。那么首先我们就需要知道,预测的答案和真实的答案差距有多大,我们需要将它量化。
假设有以下测量值:
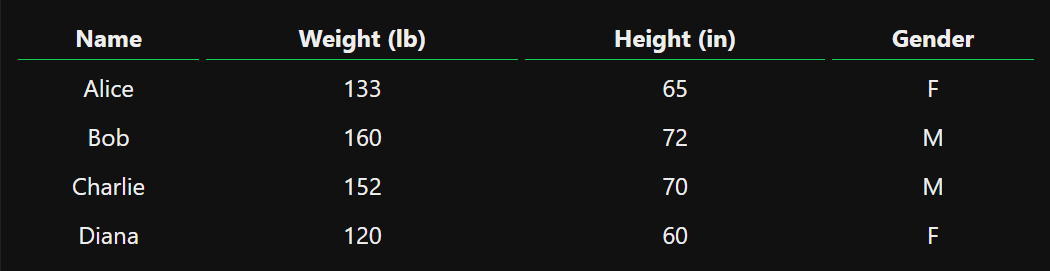 image.png
image.png
我们用0表示男性,用1表示女性。我们要训练我们的网络,根据体重和身高预测某人的性别。我们通过对数据设置偏移,让它更容易被处理:
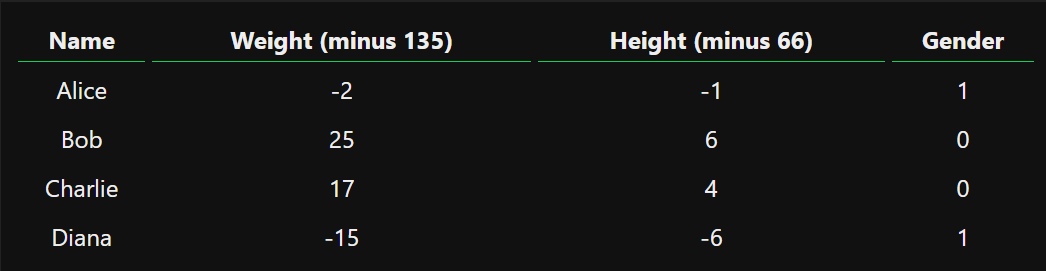 image.png
image.png
现在我们需要找到一个方法量化它的”好坏”,以训练它做的更好。这里我们使用均方误差损失(MSE)来衡量它的好坏:
$$
MSE = \frac{1}{n}\sum_{i=1}^{n}(y_{true} - y_{pred})^2
$$ 其中:
- n是样本数量,这里是4
- y代表被预测的变量,这里是性别
- ytrue是变量的真实值(“正确答案”)
- ypred是网络输出的结果,即预测值
我们可以用代码实现MSE的计算:
1
2
| def mse_loss(y_true,y_pred):
return ((y_true - y_pred)**2).mean()
|
反向传播
我们现在已经量化了我们的损失,我们现在需要通过调整网络的权重和偏差从而使得预测更加准确。我们该怎么做呢?
我们从下面这个最简单的情况开始,一点一点反推整个训练的过程
 image.png
image.png
在这次训练中,正确答案为1,预测结果为ypred。此时有: $$
\begin{align*}
MSE = \frac{1}{1}\sum_{i=1}^{n}(1-y_{pread})^2
= (1-y_{pred})^2
\end{align*}
$$
有了量化的偏差,接下来我们给网络中的每个权重和偏差都标记出来,此时我们可以写出一个多变量函数:
L(w1, w2, w3, w4, w5, w6, b1, b2, b3)
假如我们调整w1,那么损失L会怎么变化呢?也就是说我们需要求出$\frac{\partial L}{\partial
w_1}$,从而进一步调整w1以减少L
我们可以用下列过程来求出它: $$
\begin{align*}
\frac{\partial L}{\partial w_1} &= \frac{\partial L}{\partial
y_{pred}}*\frac{\partial y_{pred}}{\partial w_1}
\\
\frac{\partial L}{\partial y_{pred}} &= \frac{\partial
(1-y_{pred})^2}{\partial y_{pred}} = -2(1-y_{pred})
\end{align*}
$$ 我们想处理$\frac{\partial
y_{pred}}{\partial w_1}$,需要用h1 h2 o1
来代表神经元的输出,然后得到: $$
\begin{align*}
\frac{\partial y_{pred}}{\partial w_1} &= \frac{\partial
y_{pred}}{\partial h_1}*\frac{\partial h_1}{\partial w_1}
\\
\\
y_{pred} &= o_1 = f(w_5h_1 + w_6h_2 + b_3)
\\
\frac{\partial y_{pred}}{\partial h_1} &= w_5*f'(w_5h_1 + w_6h_2 +
b_3)
\\
\\
h_1 &= f(w_1x_1+w_2x_2+b_1)
\\
\frac{\partial h_1}{\partial w_1} &= x_1*f'(w_1x_1+w_2x_2+b_1)
\end{align*}
$$ 这里我们要用到激活函数的导数,所以对其进行求导: $$
\begin{align*}
f(x)&=\frac{1}{1+e^{-x}}
\\
f'(x)&=\frac{e^{-x}}{(1+e^{-x})^2}=f(x)*(1-f(x))
\end{align*}
$$ 现在我们可以合并计算出 $$
\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial
y_{pred}}*\frac{\partial y_{pred}}{\partial h_1}*\frac{\partial
h_1}{\partial w_1}
$$
这个反向计算偏导数的系统被称之为反向传播。现在我们可以带入数值计算出$\frac{\partial L}{\partial
w_1}=0.0214$,我们可以根据这个值来训练我们的权重。
训练
于是我们可以制定我们的训练过程了。在这里我们使用一种名为随机梯度下降的算法,它将告诉我们如何调整权重和偏差以最小化损失。它实际上就是这么个更新公式:
$$
w_1 \gets w_1 - \eta*\frac{\partial L}{\partial w_1}
$$ 这里的η指的是学习率,用来控制我们训练的速度和精度。我们对网络中的每个权重和偏差都这么做,我们的损失将慢慢减少,我们的网络将越来越准确。
我们的徐连过程将如下:
- 从数据集中选择一个样本(随机梯度下降的原理就是一次只操作一个样本)
- 计算损失相对于权重或偏差的所有偏导数
- 使用更新方程来更新每个权重和偏差
- 重复
实现一个完整的神经网络
现在我们可以实现一个完整的神经网络来实现这个训练过程了
这是我们的数据集和网络结构:
 image.png
image.png
 image.png
image.png
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
| import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def deriv_sigmoid(x):
return sigmoid(x)*(1-sigmoid(x))
def mse_loss(y_true,y_pred):
return ((y_true - y_pred)**2).mean()
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
class NeuralNetwork:
def __init__(self):
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self,x):
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self,data,all_y_trues):
learn_rate = 0.05
epochs = 5000
for epoch in range(epochs):
for x,y_true in zip(data,all_y_trues):
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
d_L_d_ypred = -2*(y_true-y_pred)
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
self.w1 -= d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1 * learn_rate
self.w2 -= d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2 * learn_rate
self.b1 -= d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1 * learn_rate
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
if epoch % 10 == 0:
y_preds =np.apply_along_axis(self.feedforward,1,data)
loss = mse_loss(all_y_trues,y_preds)
print("Epoch %d loss: %.3f" % (epoch,loss))
data = np.array([
[10.6, 5.7],
[9.8, 6.7],
[9.1, 8.0],
[8.6, 9.1],
[8.0, 9.7],
[7.5, 10.1],
[7.2, 10.8],
[7.0, 10.7],
[22.6, 20.4],
[22.1, 22.8],
[21.4, 24.3],
[20.4, 24.0],
[19.4, 23.2],
[18.7, 22.5],
[17.9, 21.6],
[17.5, 21.0]
])
all_y_trues = np.array([
1,1,1,1,1,1,1,1,
0,0,0,0,0,0,0,0
])
network = NeuralNetwork()
network.train(data,all_y_trues)
print(network.feedforward([161-150,65-50]))
|
找了下几个热心嘉宾试了一下还是很准确滴








