64:存储器层次结构与性能利用

我们学习一下现代计算机中的存储器架构，以及它的一些具体实现。我们该如何利用存储器的性能来实现对局部性的高效利用？它背后的原理又是什么呢？

存储器存储结构

不同的存储器有着不同的存储技术和存储性能，可喜的是，它们的属性很好的互相补齐各自的不足，利用这个性质，出现了一种组织存储器系统的方法，称之为存储器层次结构。

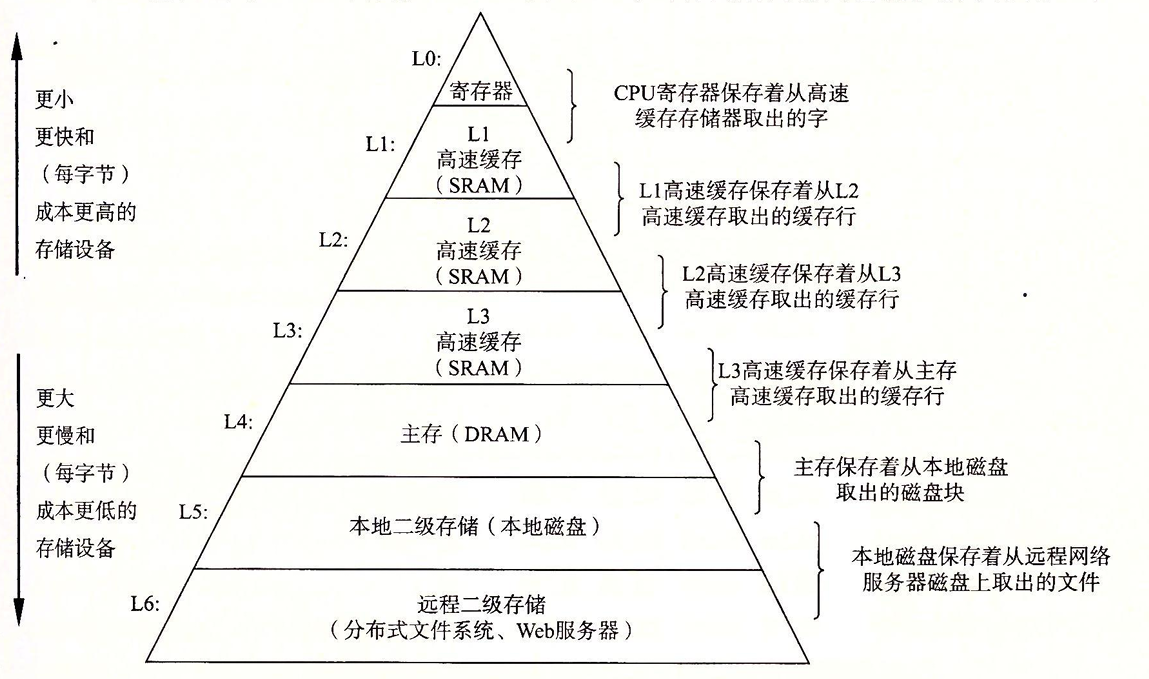
从高层往底层走，存储器的容量、成本、速度都越来越慢。所以我们以下面为基础，不断的向上层提供数据。其中我们就不得不提到存储器结构中最为关键的缓存

缓存

存储器之间的属性有着较大的差异，通常我们需要在其之间设置一个缓冲，以更好的实现数据的读取和转移。其中，高速缓存就是一种小而迅速的存储设备，它作为更大、更慢的存储器设备的数据的缓存区域。而使用高速缓存的过程我们就称之为缓存。缓存的基本原理如下：

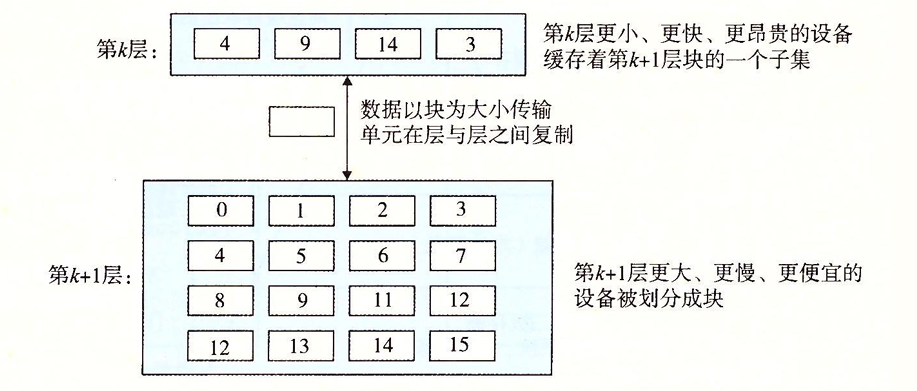
对于缓存，我们还要理解它的各个状态：

缓存命中

当程序需要k+1层的某个数据对象d时，它首先到k层中去查找，如果找到了，则此时数据d缓存命中。

缓存不命中

相反，如果k层没有找到数据d时，我们则发生缓存不命中。此时k层的缓存从第k+1层中取出包含d的块。如果此时k层的缓冲已经满了，就会覆盖其中的一个块，这个过程叫做替换/牺牲。具体替换哪个块由替换策略所决定。

缓存不命中的状态：

强制不命中（冷不命中）：此时缓存为空，无论什么数据都不会命中。
容量不命中：当前的工作集的大小大于缓存的大小。
冲突不命中：有些替换策略会将符合同一规则的块指定替换到上层换从中的指定块，这种策略比较简洁容易实现。此时就可能会出现同组的块互相冲突。类似于哈希表中的哈希冲突。

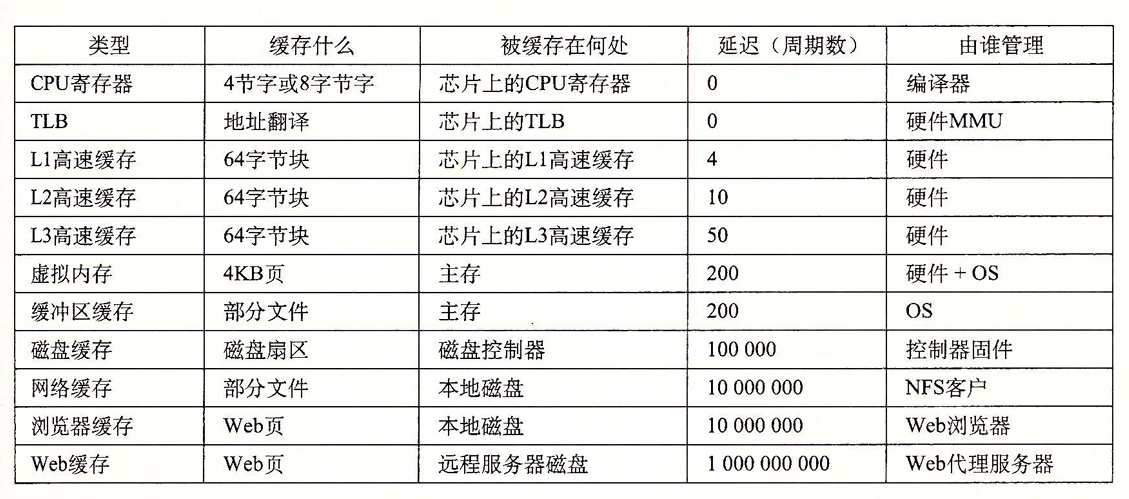
存储器层次结构的本质是，每一层存储设备都是较低一层的缓存。所以在每一层中，都需要有某种形式的逻辑来管理缓存（将缓存分块，在不同层之间传送块，判定是否命中，并处理它们），不论是硬件还是软件。下面有一张表，大致的说明了各个缓存的管理实现：

高速缓存存储器

为了更好的理解存储器缓存的原理，我们需要介绍一下高速缓存存储器的组织架构。

计算机的地址数量通常由存储器的位数所决定，当存储器的位数为m时，计算机的内存空间就有2^m个地址。而高速缓存存储器的结构如下：

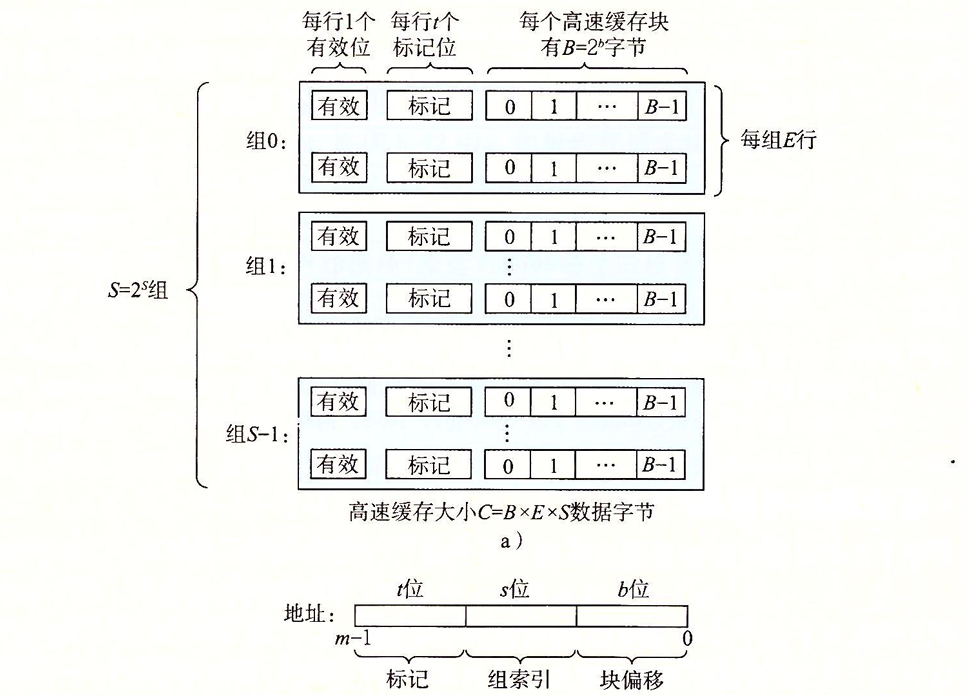
一个高速缓存存储器被分作S(2^s)个高速缓存组，每个高速缓存组有E个高速缓存行，每个高速缓存行中有B(2^b)个数据块。我们通过对地址字段进行划分，从而实现对高速缓存的定位。

当我们拿到一个地址，想要尝试从高速缓存存储器中取出一个数据块时，都要经历以下过程：

读组索引：根据地址中的s位的数据来确定数据所在的缓存组
标记比对：当数据行有效时，与其比较t位标记值，如果标记相同则确定数据存储行。
读块索引：根据地址中的b位数据确定数据在缓存块中的偏移地址。
缓存不命中：则重复上述的步骤向下取需要的数据。

你可能会好奇，为什么使用中间的几位作为组索引，而不是高位呢？这是为了避免高位的一致性从而导致连续的内存空间被分配到一个组，从而引发冲突不命中，下图很好的说明了这一点：

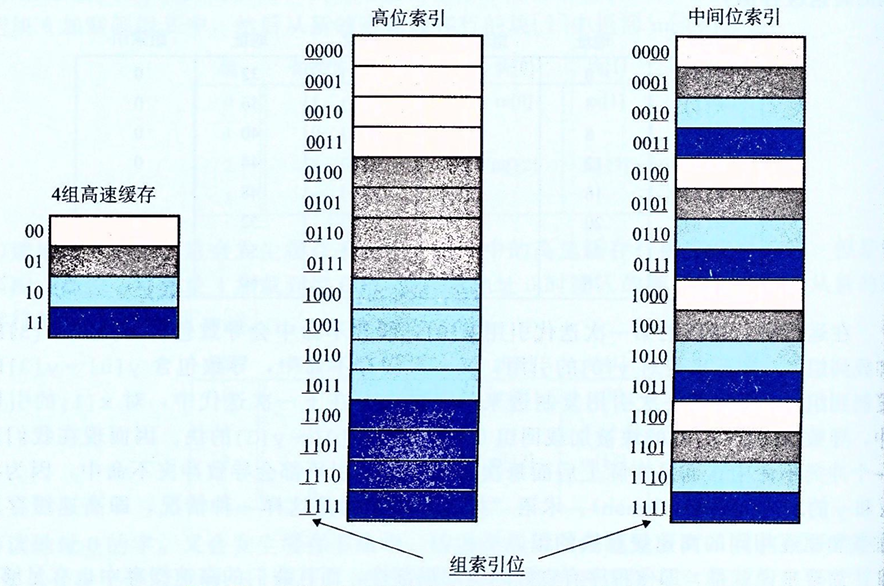
同时，根据每个组的高速缓存行的数量，也可以分成以下高速缓存存储器类型：

直接映射高速缓存

E=1，每组高速缓存行只有一行，所以不需要再组中查找对应的缓存行，且实现起来比较简单。但是对于冲突不命中的应对上效果很差，因为每个组只能取一条数据。
全相联高速缓存

S = 0，E = C/B。所有的缓存行都存储在一个组中，由于没有固定的映射关系，所以任何主存块可以存储在缓存的任何位置。灵活性很高，很好的避免了冲突的关系。但是由于结构复杂，且每次访问时，需要匹配缓存行，消耗了大量的时间，访问速度慢。
组相联高速缓存

相当于直接映射和全相联的中和版本。每个组有一定的缓存行。

高速缓存层次结构分析

我们给出一个真实的高速缓存层次结构

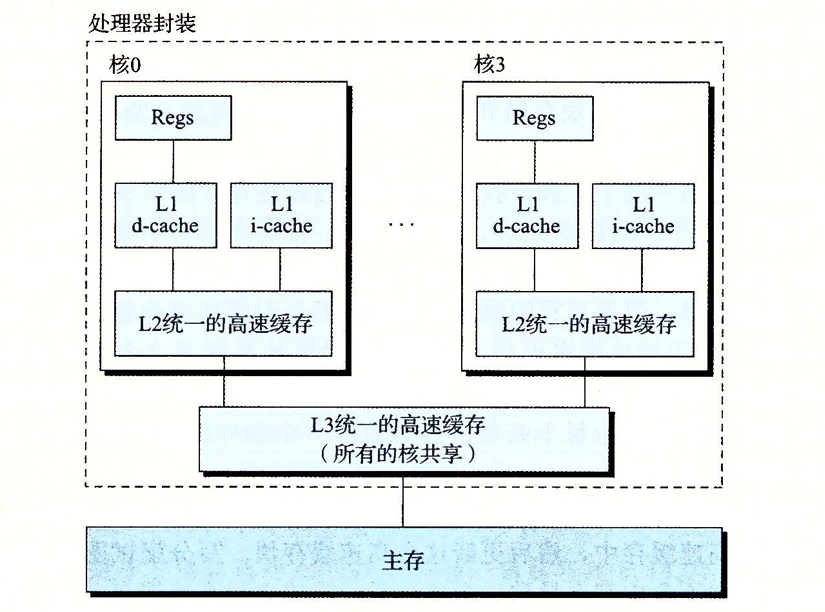
实际上高速缓存存储器不仅存储数据，同时存储着指令，只不过指令是只读的，数据则可读可写。芯片上的每个核有着自己的高速缓存，同时共享一个高速缓存和主存。在复杂的资源共享管理下，实现工作

高速缓存参数的性能影响

定性的分析高速缓存的影响参数：

高速缓存大小

较大的高速缓存可以提高缓存的命中率，但也意味着会造成更大的运行开销，这也是为什么越上层的存储器越小，这可以减少访问的时间。
块大小

大的块可以更好的利用程序中的空间局部性。但是在缓存空间给定的情况下，较大的块会导致较少的缓存内存行，会加剧数据冲突。从而导致时间局部性所受到的损耗大于空间局部性带来的好处。
相联度

即高速缓存行数E的选择，较高的相联度可以减少冲突不命中导致的不命中处罚，但是访问速度低，而且较大的块也会导致更严重的不命中处罚。而较低的相联度虽然访问速度快，但是也会导致更多的不命中处罚。所以需要根据不同的情况选择不同的相联度。

在L1中，通常使用相联度低的存储方式，因为不命中的处罚较小（数据较少）。但是对于底层的主存等区域，每次不命中的处罚很严重，所以要提高相联度，尽可能的减少不命中。
写策略

直写（立即将高速缓存块写入第一层的存储器中）比较容易实现，而且可以使用写缓冲区进行内存更新，但是会导致总线的流量增大。写回（尽可能的推迟更新，只有该块被替换的时候才将数据块更新到第一层的存储器中）引起的传送会更少。此外，越往底层走，传送的时间更长。所以在下层，会尽可能的使用写回。

局部性

一个具有良好局部性的程序，通常会有着更好的效率。它们倾向于使用离它们较近的数据项，或是最近引用过的数据项，这被称为局部性原理。

局部性别分为空间局部性和时间局部性。对于一个良好的时间局部性程序，被引用过一次的内存位置会在不久后再次被引用。对于一个良好的空间局部性程序，如果一个内存位置被使用，那么它领近的内存位置也会被使用。

对程序数据引用的局部性

我们以一个简单的程序为例：

int sumvec(int v[N]){
    int i,sum=0;
    for(i=0;i<N;i++){
        sum += v[i];
    }
    return sum;
}

对于sum，由于它在每次迭代中都被使用，所以我们称它有良好的时间局部性，但是它是一个标量，所以不存在空间局部性。对于向量v，它是被顺序读取的，所以我们称它有良好的空间局部性，但是由于每个位置只访问一次，所以我们说v的时间局部性很差。

我们说像sumvec这样顺序访问一个向量每个元素的函数，是具有步长为1的引用模式（相对于元素的大小）。有时我们称步长为1的引用模式为顺序引用模式。一个连续向量中，每隔k个元素进行访问，就称为步长为k的引用模式，步长越长，空间局部性就越差。

取指令的局部性

程序指令存放在内存中，CPU需要取出这些指令，所以我们也可以评价一个程序关于取指令的局部性。对于循环，通常是在连续的空间中进行的，所以它有良好的空间局部性，由于它会被反复调用，所以也有着良好的时间局部性。举个例子：

// clang-format off
hotblock1:
    Stmts; // <-- 热！
    if (/* 边界条件不成立 */ true)
        goto hotblock2; // 经常发生！ ------+
coldblock:                           /*   |   */
    Stmt; // <- 冷                        |
    Stmt; // <- 冷                        |
    Stmt; // <- 冷                        |  跨越了大量指令，代价高昂！
    Stmt; // <- 冷                        |
    Stmt; // <- 冷                        |
    Stmt; // <- 冷                        |
    Stmt; // <- 冷                        |
hotblock2:                          /*    |   */
    Stmts; // <- 热！           <----------+

// clang-format off
hotblock1:
    Stmts; // <-- 热！
    if (/* 边界条件 */ false)
        goto coldblock; // 很少发生
hotblock2:                         /*   |  低代价！  */
    Stmts; // <- 热！  <-----------------+
coldblock:
    Stmt; // <- 冷
    Stmt; // <- 冷
    Stmt; // <- 冷
    Stmt; // <- 冷
    Stmt; // <- 冷

代码区别于程序数据的一点在于，在运行时它是不能被修改的，CPU只从内存中读取指令，并不修改它。

编写高速缓存友好的代码

明白了高速缓存的工作原理之后，我们可以更准确的描述局部性了，局部性较好的程序通常意味着较高的命中率，不命中率较低的程序往往运行的会更快。所以编写局部性好的程序实际上是编写对高速缓存友好的程序。

下面就是我们用来确保代码高速缓存友好的基本方法：

让常见的情况运行得快，程序通常把大部分时间花在少量的核心函数上，而这些函数通常把大部分时间花在了少量的循环上，所以要把注意力击中在核心函数的循环上，忽略其他部分。
尽量减少每个循环内部的缓存不命中数量，在其他条件相同的情况下（加载存储操作次数），不命中率低的程序通常循环运行的更快。

同时还有几个重要问题：

对局部变量的反复引用是好的，因为编译器能够将它们缓存在寄存器中（时间局部性）
步长为1的顺序引用是好的，因为存储器层次结构中所有层次上的缓存都是讲数据存储为连续的块（空间局部性）

我们这里以n*n矩阵相乘为例：

让 C = A x B，我们通常会写出以下代码：

for(int i=0;i<n;i++){
    for(int j=0;j<n;j++){
        for(int k=0;k<n;k++){
            C[i][j] = A[i][k]*B[k][j];
        }
    }
}

根据i,j,k不同的循环顺序，实际上我们可以写出六个版本的矩阵乘法，但是它们是否互相等价呢？

我们可以分析，对于循环的过程中，我们总是希望步长是尽可能小的。所以我们优先考虑B矩阵的数据，对于B[k][j]的迭代，我们希望是kj顺序的，此时是顺序执行，空间局部性良好。对于左边的A[i][k]，我们应该优先考虑对k的迭代，以保证步长尽可能的小，所以使用ik顺序迭代。综上所述，ikj循环才是性能最好的，其他的就不过多赘述。反向分析即可。

在对程序空间局部性的分析过程中，我们要考虑到缓存时是行缓存存储的，所以应该尽可能的让要使用的数据在空间上是连续接近的。同时将目光聚焦于内循环（程序中迭代次数最多的代码块）中，以获得最好的局部性。对于新引入的数据对象，我们也应该多使用它，利用好时间局部性。