61:程序性能优化(2)

上次我们分别从简单的过程调用的优化到了机器级层面的关键路径优化。在此基础之上，我们可以尝试更进一步的优化。

循环展开

循环展开通过增加每次迭代计算的元素的数量，减少循环的迭代次数。它从两个方面改进了程序的性能：

减少了循环索引的计算和条件分支的判断
提供了一些方法，进一步的变化代码，减少整个计算中关键路径上的操作数量

比如下面这个例子：

void combine5(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    for(i=0;i<limit;i+=2)
        acc = (acc OP data[i]) OP data[i+1];
    
    for(;i<length;i++)
        acc = acc OP data[i];
    *dest = acc;
}

这里我们每次迭代都进行了两次迭代，我们可以看到一定程度上的性能优化：

实际上循环展开也有许多需要注意的地方，比如循环展开的边界条件。我们设我们的按k次进行迭代，也就是说每次会将从i到i+k-1的数据进行计算，但是可能会出现一个情况。我们的原迭代次数可能无法被k整除，这意味着我们可能会出现漏处理的情况，需要额外设置一个循环。那么第一个循环的边界应该到哪里为止呢？

1	i+k-1 < n --> i < n-k+1 --> limit = n-k+1

推断可知i只能小于我们得到的limit，以确保程序能够正常迭代。剩下的未能完全迭代的部分，我们使用另一个循环来继续计算。

但是循环展开的次数越多，性能的优化效果就越好吗？我们看到并非如此：

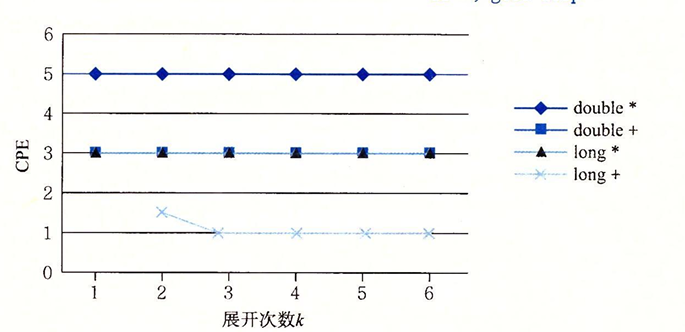
要理解为什么程序没法进一步的优化，我们需要分析程序的关键路径，我们将k=2 data_t=double OP=*时的关键代码转化成图形化表示：

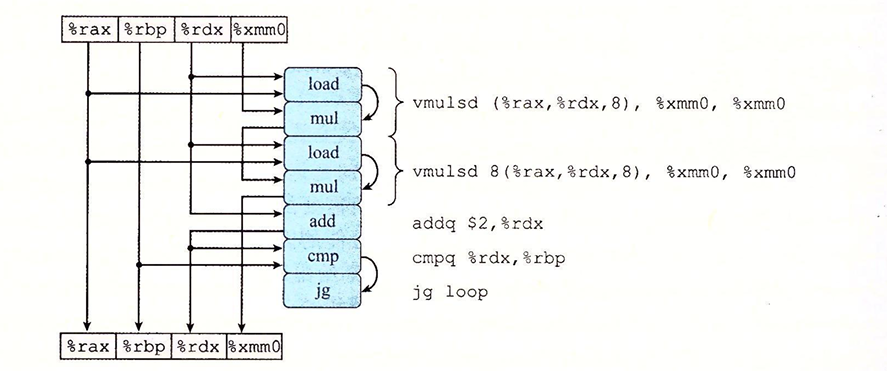
我们进一步的化简，可以看到关键路径的状态：

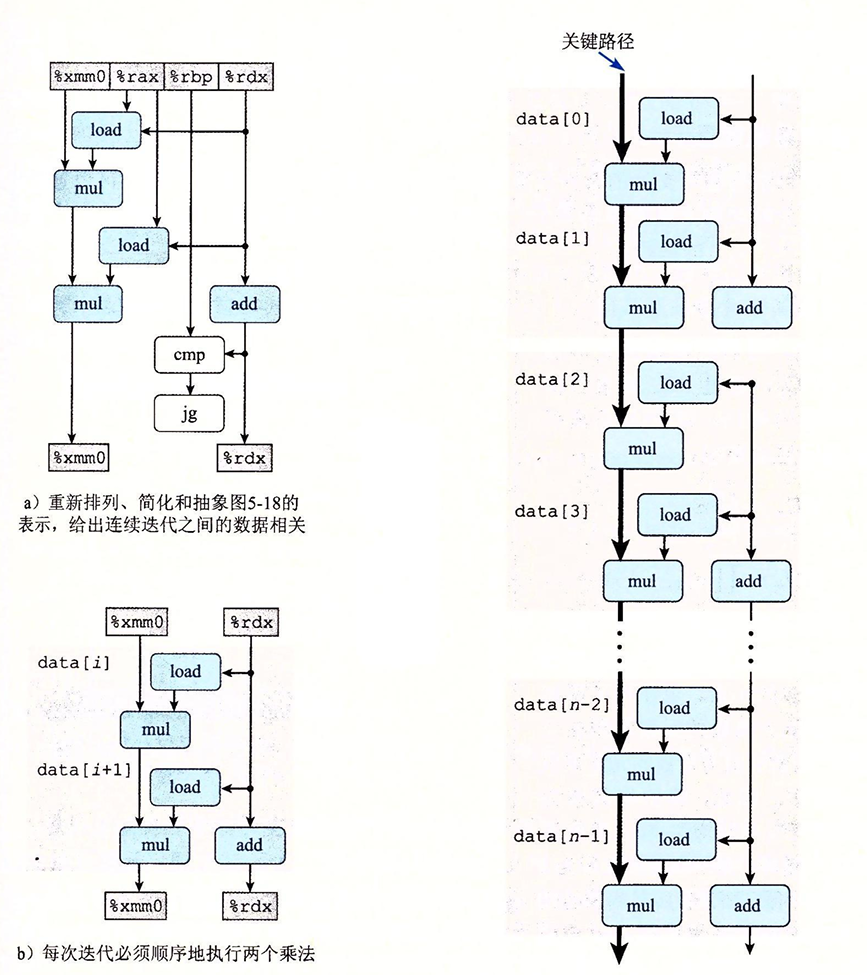
无论怎么展开，关键路径上还是有n个mul操作，由于数据的依赖关系，这里的乘法操作在每次展开中实际上并不能并行处理。为了进一步的提高程序的性能，我们要想办法提高数据的并行性。

提高并行性

硬件通常有多个相同的硬件组成，实际上硬件有更高速率执行加法和乘法的潜力，但是我们的代码无法实现这个功能，这是因为我们将累计的值放在一个单独的变量中，在前一个操作结束前，我们都无法进行下一个整数操作，所以我们需要相办法打破这种顺序相关，来更好的利用硬件的并行性能。

多个累计变量

对于一个可交换可结合的合并运算来说，我么可以通过将一组合并运算拆分成多个部分，最后合并结果，来提高性能，比如对于：

P_n = a₁ * a₂ * …… * a_n 我们可以将其拆分成 PO_n = a₁ * a₃ * …… * a_2i+1 和 PE_n = a₂ * a₄ * …… * a_2i，最后合并得到 P_n = PO_n * PE_n

我们可以用代码实现，这种既做循环展开，又做两路并行的效果：

void combine6(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;
    
    for(i=0;i<limit;i+=2){
        acc0 = acc0 OP data[i];
        acc1 = acc1 OP data[i+1];
    }
    	
    for(;i<length;i++)
        acc0 = acc0 OP data[i];
    *dest = acc0 OP acc1;
}

性能如下：

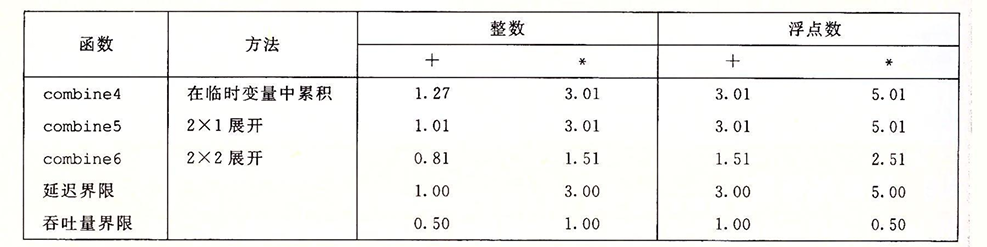
我们的增加并行计算后的程序性能超过了延迟界限，相较于之前提升了两倍，这意味着我们很好的利用了并行计算的优势，我们可以根据对关键路径的分析中很好的看到这一点：

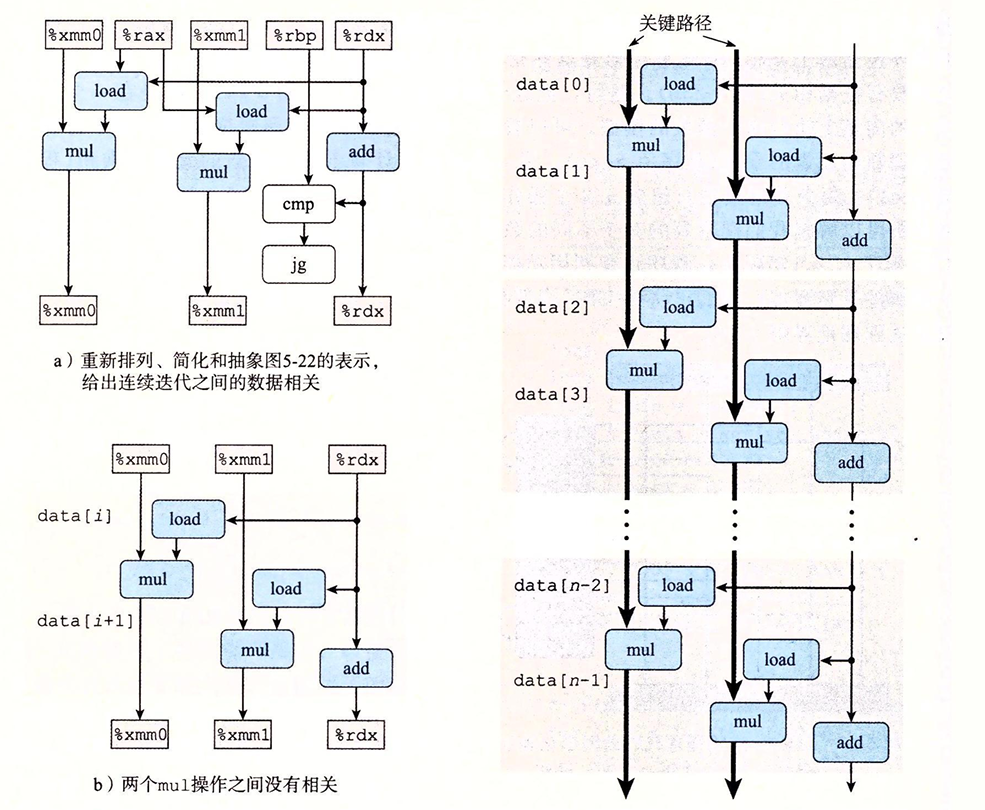
combine6中的两路并行优化将原来的一条关键路径拆分成了两条关键路径，现在每条关键路径上的mul操作变成了n/2次。使得程序的性能极大的提升，对于我们进行k*k的优化，我们可以在下图中看到效率的提升：

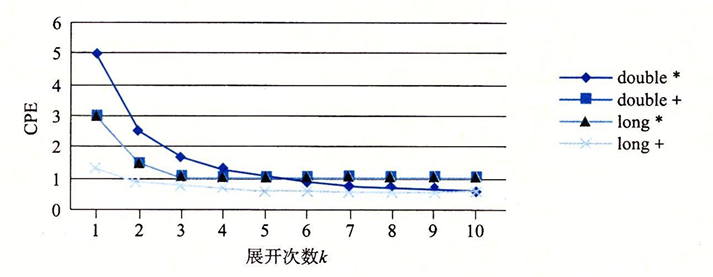
可以看到随着k的增加，甚至可以使程序的性能逼近吞吐量的界限。

但是，这样的并行计算一定很好吗？它也有着一定的副作用，受四舍五入和溢出的影响，可能会一定程度上改变程序的行为，造成一定的误差。需要酌情处理。

重新结合变换

现在我们需要探讨另一种打破顺序相关的方式以将性能提高到延迟界限之外。我们只需进行对combine5的循环逻辑进行微小的合并变换即可得到：

void combine7(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    for(i=0;i<limit;i+=2)
        //原：acc = (acc OP data[i]) OP data[i+1];
        acc = acc OP (data[i] OP data[i+1]);
    
    for(;i<length;i++)
        acc = acc OP data[i];
    *dest = acc;
}

看上去并没有发生什么改变，但是实际测量的性能却得到了很好的提升：

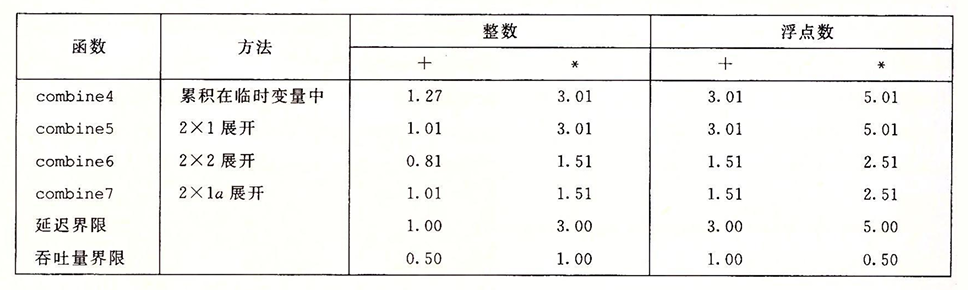
我们还是分析关键路径：

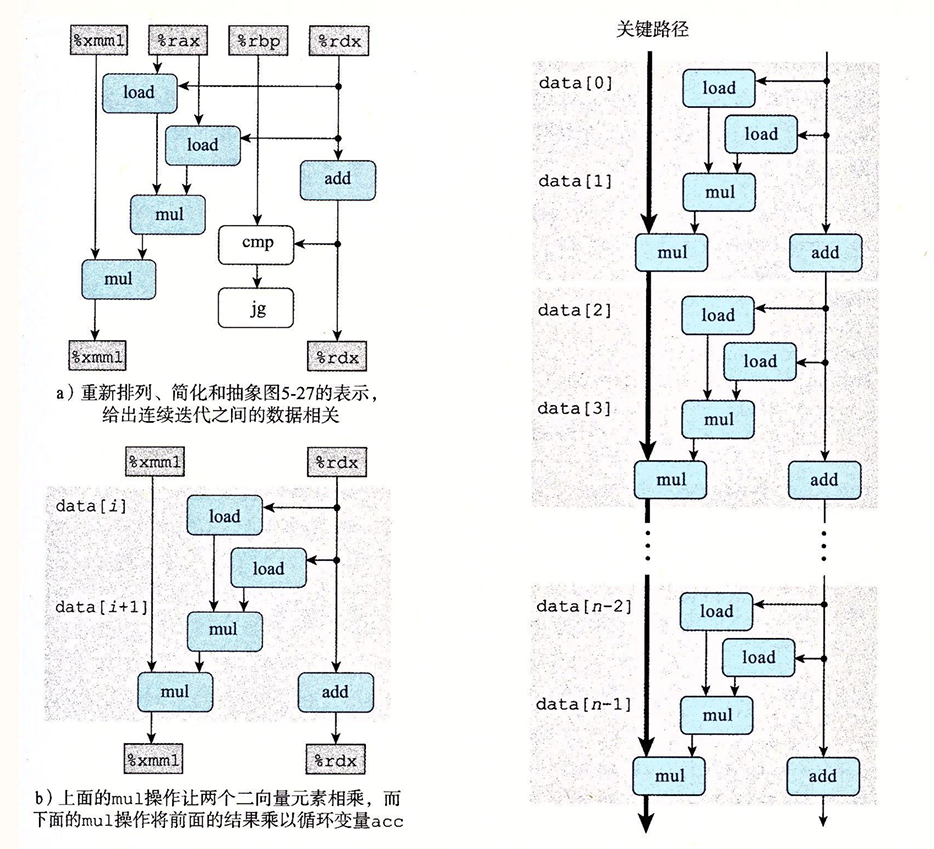
我们可以看到，每次迭代的第一个乘法实际上不存在顺序相关的问题，它的每次计算不依赖于上一次的迭代寄存器，所以关键路径上只有一次乘法操作，另一次乘法操作始终可以并行操作。所以通过这种方式，关键路径上只有n/2次mul操作。

随着展开次数的增多，程序的性能也可以接近吞吐量界限。总的来说重新结合变换会减少计算中关键路径上操作的数量，通过更好的利用功能单元的流水线能力得到更好的性能。要注意的问题和上面一样。

优化合并小结

通过以上的例子，我们应该意识到现代处理器强大的计算能力，可是现代编译器因为种种原因始终不能完全的利用这些能力，但是我们可以按一些非程式化的方式来编写程序以激发这些能力。