Ylin's Blog
0%

56:mov指令的图灵完备性

发表于 更新于 分类于 ，
本文字数： 4.2k 阅读时长 ≈ 4 分钟

文章原文：mov is Turing-complete ——by Stephen Dolan，Computer Laboratory, University of Cambridge

不使用特殊的寻址模式，代码自修改，和运行时生成代码。用mov实现图灵完备的模拟器

介绍

我们在学习下x86的指令集中我们时常会用到MOV指令。我们通常使用它的多种寻址模式：

  • 用于内存数据的加载和存储
  • 加载立即数到寄存器中

但是它并不具备比较和分支跳转的功能，所以我们一般认为MOV不是图灵完备的

但是实际上在x86的处理器中，我们可以通过mov来加载或者自修改代码来实现图灵完备性，但是这并不是我们想要的。

执行有限数量的mov指令将会在有限时间内结束。为了验证它的图灵完备性，所以我们需要无限循环。因此我们的图灵机将由一系列mov指令组成，执行完成后无条件跳转到第一条指令继续执行。

机器模型

我们将使用一个简单的抽象机器模型，我们介绍其组成：

  • 一个由字组成的随机存储内存：每一个字可以存储一个内存地址或一个偏移值（偏移值只能是0或1，其中偏移值不被视作一个有效的内存地址）
  • n个寄存器R1 R2 … Rn ：我们暂时假设我们会用到很多寄存器，不过我们之后会讨论怎么减少使用寄存器的数量
  • Intel格式的mov指令：
    • 加载立即数：mov R_dest,c
    • 索引加载：mov R_dest,[R_src+R_offset]
    • 索引存储：mov [R_dest+R_offset],R_src
  • 内存：内存被逻辑的划分为单元，这些单元都是成对的相邻的字。我们的加载存储操作本质可以视作是在这些单元中进行的。我们的指令从偶数的地址开始，我们使用两个寄存器，其中一个用来确定单元的地址R_src，另一个用来确定使用哪个字R_offset

使用这些组成，我们就可以模拟一个由mov进行的图灵机了

表示图灵机

我们使用一个元组来描述图灵机M:

1
M = (Q,q0,∑,σ0,δ)
  • Q是一个有限状态集，其中指定一个起始状态q0∈Q
  • ∑是有一个有限符号集，其中指定一个空白符号σ0∈∑
  • δ是一个转换函数，图灵机根据当前的状态和读取到的符号决定：
    • 写入带上的新符号（Σ 中的一个符号）
    • 磁头移动的方向（左 L 或右 R）
    • 转换到的新状态（Q 中的一个状态）

图灵机有一个磁带，由无限多个位置组成，每个位置上有一个单独的符号。图灵机会持有一个当前的状态q0，和当前的位置（初始位置为磁带的最左边，磁带向右无限延申）。每个磁带的位置都被初始化为空白符号σ0。

图灵机会反复计算转换表δ，如果当前的状态和读取到的符号的情况在δ中并没有被定义，机器将会终止。如果是已有定义（σ，d，q），那么机器会将当前的状态设置为q，将σ写入当前的位置，同时根据d来决定纸带的跳转方向（如果d=L向左，如果d=R向右），然后机器继续运行。

我们可以在内存单元中表示我们的符号集。我们首先要将图灵机的符号集∑映射到每个单元中，符号集中的每个符号都对应一个内存的单元，这些单元的地址被描述为S1，S2，…，S|∑|，其中|∑|是符号集的数量，即大小。每个单元Si的内容是未指定的，他可能包含任何值。但是对于第一个内存单元S1，它的值始终是空白符号σ0。

接下来我们要在计算机内存中表示图灵机的状态和转换表。转换函数实际上就是根据当前给定的状态和当前读取的符号，来给出图灵机要进行的操作。我们可以理解为δ(σ,q) = (σ',d',q')。在内存中，每个状态q被表示为出转换的列表。每个做出转换被表示为一个包含四个元素的元组(σ,σ‘,d’,q’)，其中：

  • σ表示当前状态下图灵机读取到的符号。在内存中，这个符号被表示为对应单元Si的地址
  • σ’表示图灵机在当前单元写入的新符号。在内存中，这个符号被表示为对应单元Sj的地址
  • d’表示图灵机的读写头移动的方向。在内存中，这个状态被表示为一个数字，0L1R
  • q’表示图灵机转换后的新状态。在内存中，对应出转换列表的地址

我们用一张图片来描述这个过程：

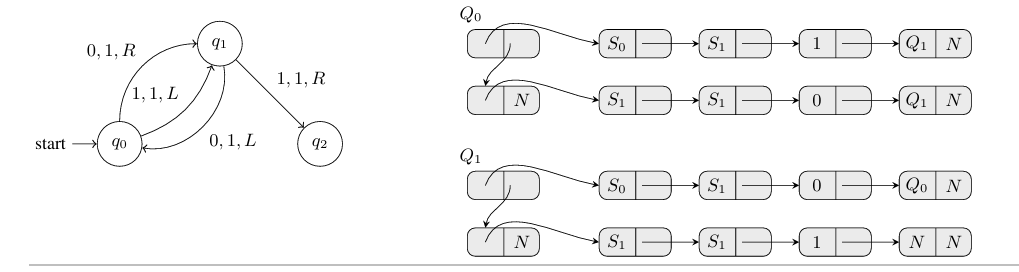
image.png

这个Q0和Q1则是转换的规则，我们可以根据它确定图灵机接下来的行为。

内存中的其他单元则用来表示我们图灵机中的磁带。我们假设磁带是无限长的（尽管现实中的内存地址是有限的），我们将单元按T1,T2,…来进行，命名使得Tn的中的字就是S1的地址，Tn+1中的字是Tn+1的地址

通过这个方式，我们可以将T1视作一个无限的表的起始，且无限的表中的每一个元素的初始值为S1。在讨论图灵完备的过程中，我们通常只关心计算的过程，而忽略输入和输出。我们假设在程序开始前，输入是一串符号队列，从T1到Tn。而输出则是在指令执行结束后，纸带上的值就是输出。

比较和条件语句

计算的基础之一就是分支，根据运行的值选择下一个要执行的操作，我们接下来尝试用mov来实现它。

我们可以用一下方式来比较A和B是否相等：

1
2
3
mov [R_i],0
mov [R_j],1
mov R_k,[R_i]

我们可以根据R_k的值判断R_i和R_j是否相等。如果R_i和R_j相等，那么相当于向同一个地址写入了两次值，如果不相等，[R_i]处的值就不会被修改。所以A=B->1 A!=B->0

我们也可以比较一个指定的值和N是否相等：

1
2
3
4
5
mov X,[R_i]
mov [N],0
mov [R_i],1
mov R_j,[N]
mov [R_i],X

原理同上，只不过这里我们用X保存了R_i地址上的数据

这个原理允许我们实现比较语句，结果要么是0要么是1。我们可以用这些结果去选择不同的值。如我们上面所说的在一个单元中我们可以根据index(即R_k)来计算使用哪个字。假如N是其中一个单元格的地址，我们就可以利用比较的结果来判断读取单元中的哪个字：

1
2
3
mov [N],R_i
mov [N+1],R_j
mov R_l,[N+R_k]

通过这些操作我们已经可以模拟一个图灵机了

模拟图灵机

  • 我们使用T来存储当前的要测试的转换（存储了转换规则的地址）
  • 使用S来存储当前读取的符号（用来查找规则）
  • 使用L来代表当前位置左侧磁带部分的列表
  • 使用R来代表当前位置右侧磁带部分的列表（LR可以用来模拟读写头移动的操作）

磁带由L+S+R组成

程序的开始，T会存储Q0的地址，S存储T1的地址，L存储N的地址（代表空列表，用于逆向存储左边磁带的部分。这样最近的位置总是左边的列表的第一个元素，这样向左处理无需移动整个列表），R存储T2的地址（初始时为T，即磁带上除了第一个位置外所所有位置的列表）。L和R寄存器中的列表被视作栈，当图灵机向右移动时，当前的符号S被推入L队列中，R队列中的符号被弹出到S。同时由于我们会经常用到N，所以我们设置寄存器N始终保存地址N。

介绍完这些前置的条件，我们现在开始实现图灵机：

首先我们需要根据当前符号S和转换规则T来判断是否应该触发转换：

1
2
3
4
5
6
mov X,[T]		;获取转换规则
mov X,[X]		;获取触发符号
mov Y,[S]		;获取当前符号
mov [Y],0		;比较当前符号与触发符号
mov [X],1
mov M.[Y]

再此基础之上，我们构造功能来更新当前符号，当M=1(匹配)时触发

1
2
3
4
5
6
7
8
mov X,[T]		;获取转换规则（触发符号,新符号,...）
mov X,[X+1]		;跳过触发符号
mov X,[X]		;加载新符号	
mov Y,[S]		;记载旧符号
mov [N],Y		;选择新旧符号
mov [N+1],X
mov Z,[N+M]
mov [S],Z		;写入新符号

接着，我们加载纸带的移动方向：

1
2
3
4
mov D,[T]		;获取转换规则（触发符号,新符号,方向,...）
mov D,[D+1]		;跳过触发符号
mov D,[D+1]		;跳过新符号
mov D,[D]		;加载方向

然后根据D的值0左1右。将单元添加到磁带栈上的过程是，先将磁带栈的顶端写为[S+1]，然后修改磁带栈寄存器为S，下面这个是将S压入栈顶的过程：

1
2
3
4
5
6
7
8
9
10
mov [N],R		;获取[S+1]的值（[S+1]就是下一个要被读取的符号）
mov [N+1],L
mov X,[N+D]
mov [S+1],X
mov [N],L		;确定L的值
mov [N+1],S
mov L,[N+D]
mov [N],S		;确定R的值
mov [N+1],R
mov R,[N+D]

我们必须确认只有在转换规则匹配的时候才有移动。如果不匹配的话，我们需要翻转刚刚D的值，以复原移动

1
2
3
4
5
6
mov [N],1		;X~=D
mov [N+1],0
mov X,[N+D]
mov [N],X 		;选择X或者D
mov [N+1],D
mov D,[N+M]

接下我们将根据D的值将栈顶的值弹出至S:

1
2
3
4
5
6
7
8
9
10
mov [N],L		;获取S的值
mov [N+1],R
mov S,[N+D]
mov X,[S+1]		;获取L或R的栈顶元素
mov [N],X		;为L赋值
mov [N+1],R		;这里让L=R看起来很奇怪，实际上刚刚更新了当前的S_current = R_old，此时R栈顶尚未更新
mov L,[N+D]		
mov [N],R		;当左移时
mov [N+1],X
mov R,[N+D]

如果M是匹配的话就会正常移动，不匹配就会不动。然后接下来我们要更新图灵机的状态：

1
2
3
4
5
6
7
8
9
mov X,[T+1]		;加载下一个转换列表的地址
mov Y,[T]		;获取转换规则（触发符号,新符号,方向,下个状态的转换列表）
mov Y,[Y+1]		;跳过触发符号
mov Y,[Y+1]		;跳过新符号
mov Y,[Y+1]		;跳过方向
mov Y,[Y]		;获取下个状态的转换列表的地址
mov [N],X
mov [N+1],Y
mov T,[N+M]

不过有时候也会出现没有合适的转换规则的情况，这个时候我们需要做一个验证，检测是否到达了某个状态列表的末尾：

1
2
3
4
5
mov X,[T]
mov [N],0	;这里N代表空列表的地址，所以用T与N比较
mov [T],1
mov H,[N]
mov [T],X

如果H=0我们需要停止机器，我们通过从无效地址0中读取来实现这一点：

1
2
3
4
mov [N],0		;从0或N中选择
mov [N+1],N		
mov X,[N+H]
mov X,[X]		;加载0或N

如果程序地址没有终止程序，说明我们找到了下一个转换规则并将指针指向了T。同时我们将当前符号存放在S中。因此我们现在又一次的处于了一个合适的状态中，我们跳转到开始，再次重复上述的过程，这就是一个图灵机的完整的行为过程：

1
jump start