继续冲
介电质材料
乍一听可能感觉很厉害，但实际上水，玻璃，钻石一类的材料都属于介电质，他们通常有以下特点：
- 不导电：但会光会与该材料发生相互作用，主要表现有 反射与折射
- 折射率：是材料特有的属性，决定光线进入材料时的弯曲程度，不同的材料有不同的折射率
当光线击中他们时，会分成反射光线和折射（透射）光线。我们将通过随机选择的反射换和折射来处理这个情况，并确保每次交互只生成一个光线。
当光线从一种材料的周围环境进入该材料本身，如(玻璃和水)时，会发生折射，光线会弯曲。折射光线的弯曲程度由材料的折射率决定。通常，折射率n是一个描述光线从真空进入材料时弯曲程度的单一值。当一种透明材料嵌入另一种透明材料中时，可以用相对折射率来描述折射：物体的折射率/环境的折射率。如渲染一个水下的玻璃，那么其有效折射率为玻璃的折射率/水的折射率
斯涅尔定律
折射一般由斯涅尔定律来描述：
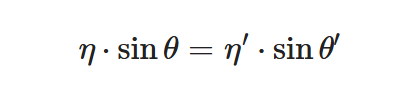image.png
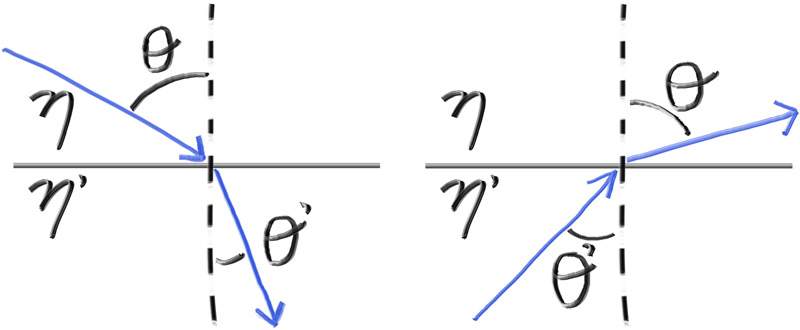
这里的符号我不好用Latex打出来，所以折射率用eta来描述，并且这里结合一张图来描述：
img
为了确定折射光线的方向，我们需要解出sin(theta’)：
1
| sin(theta0) = eta/eta0 * sin(theta)
|
我们可以将折射光线分解成垂直法线方向和平行法线方向：
1
2
3
| R = R_parallel + R_vertical
后续简写成:
R = R_p + R_v
|
根据斯涅尔定理，折射光线的垂直分量与入射光线的垂直分量也成比例：
所以可以计算出
1
2
3
4
| R_p = (R*n)*n
R_v = R - R_p = R - (R*n)*n
R*n = -cos(theta0)
R_v0 = eta/eta0 * (R + cos(theta)*n)
|
由于单位向量下，|R|^2 = |R_p|^2 + |R_v|^2，我们有：
1
2
3
4
| R_p0 = -sqrt(1 - |R_v0|)*n
R_v0 = eta/eta0 * (R + (-R*n)*n)
R0 = R_p0 + R_v0
|
我们可以写出向量的折射函数：
1
2
3
4
5
6
7
|
inline vec3 refract(const vec3& uv,const vec3& n,double etai_over_etat){
auto cos_theta = std::fmin(dot(-uv,n),1.0);
vec3 r_out_perp = etai_over_etat * (uv + cos_theta*n);
vec3 r_out_parallel = -std::sqrt(std::fabs(1.0-r_out_perp.length_squared()))*n;
return r_out_perp + r_out_parallel;
}
|
在此基础上，我们可以创建出我们的介电质材料类：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class dielectric : public material{
public:
dielectric(double refraction_index) : refraction_index(refraction_index) {}
bool scatter(const ray& r_in,hit_record& rec,color& attenuation, ray& scattered) const override {
attenuation = color(1.0,1.0,1.0);
double ri = rec.front_face ? (1.0/refraction_index) : refraction_index;
vec3 unit_direction = unit_vector(r_in.direction());
vec3 refracted = refract(unit_direction,refracted,ri);
scattered = ray(rec.p,refracted);
return true;
}
private:
double refraction_index;
};
|
然后我们更改main函数重新渲染看看效果：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int main(){
...
auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto material_left = make_shared<metal>(color(0.8, 0.8, 0.8),0.3);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2),0.0);
auto material_front = make_shared<dielectric>(1.50);
world.add(make_shared<sphere>(point3( 0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3( 0.0, 0.0, -1.5), 0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3( 1.0, -0.3, -1.0), 0.2, material_right));
world.add(make_shared<sphere>(point3(0.0,-0.2,-1.0),0.3,material_front));
...
}
|
image.png
可以看到中间一个怪怪的就是我们的玻璃球体，现在它只有折射属性，所以看起来怪怪的，中间的小黑点则是因为其光线追踪到的未被遮挡的阴影。
全反射
如果介电材料只是折射到话，也会遇到一些问题，对于一些光线角度，它的计算并不符合斯涅尔定理。如果光线以较大的入射角进入交界处，可能会以大于90°的角度折射出来，这显然是不可能的，所以这里我们将要用到我们高中所学的知识——全反射，来解决这个问题。
至于判断什么时候计算，我们计算一下折射角度的sin值，如果sin值大于1，就说明发生全反射。我们就不用折射函数来计算，用反射函数来计算出射光线。我们可以写出如下代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| bool scatter(const ray& r_in,hit_record& rec,color& attenuation, ray& scattered) const override {
attenuation = color(1.0,1.0,1.0);
double ri = rec.front_face ? (1.0/refraction_index) : refraction_index;
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = std::fmin(dot(-unit_direction,rec.normal),1.0);
double sin_theta = std::sqrt(1.0 - cos_theta*cos_theta);
bool cannot_refract = ri * sin_theta > 1.0;
vec3 direction;
if(cannot_refract)
direction = reflect(unit_direction,rec.normal);
else
direction = refract(unit_direction,rec.normal,ri);
scattered = ray(rec.p,direction);
return true;
}
|
我们现在采用这个新的dielectric::scatter()函数渲染先前的场景，会发现没有任何变化。这是因为给定一个折射率大于空气的材料的球体，不存在入射角会导致全反射。这是由于球体的几何形状，入射和出射的角度经过两次折射还是一样的。
所以我们这里模拟空气的折射率和水一样，然后把球体的材料改为空气，所以我们设置它的折射系数为index of refraction of air / index of refraction of water，然后我们渲染试试：
image.png
Schlick近似
实际生活中，光线击中透明材质表面时，一部分光会反射，还有一部分光会折射，这个比例取决于入射角和两种介质的折射率。这个现象叫做菲尼尔效应，其严格的计算十分复杂，但好在我们有一个名为Schlick近似的计算方式，它是简化的替代方案，而且十分简便。我们可以看下它的内容：
image.png
我们在此基础之上可以改进我们的dielectric类：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class dielectric : public material{
public:
dielectric(double refraction_index) : refraction_index(refraction_index) {}
bool scatter(const ray& r_in,hit_record& rec,color& attenuation, ray& scattered) const override {
attenuation = color(1.0,1.0,1.0);
double ri = rec.front_face ? (1.0/refraction_index) : refraction_index;
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = std::fmin(dot(-unit_direction,rec.normal),1.0);
double sin_theta = std::sqrt(1.0 - cos_theta*cos_theta);
bool cannot_refract = ri * sin_theta > 1.0;
vec3 direction;
if(cannot_refract || reflectance(cos_theta,ri) > random_double())
direction = reflect(unit_direction,rec.normal);
else
direction = refract(unit_direction,rec.normal,ri);
scattered = ray(rec.p,direction);
return true;
}
private:
double refraction_index;
static double reflectance(double cosine,double refraction_index){
auto r0 = (1 - refraction_index) / (1 + refraction_index);
r0 = r0*r0;
return r0 + (1-r0)*std::pow((1 - cosine),5);
}
};
|
对比一下：
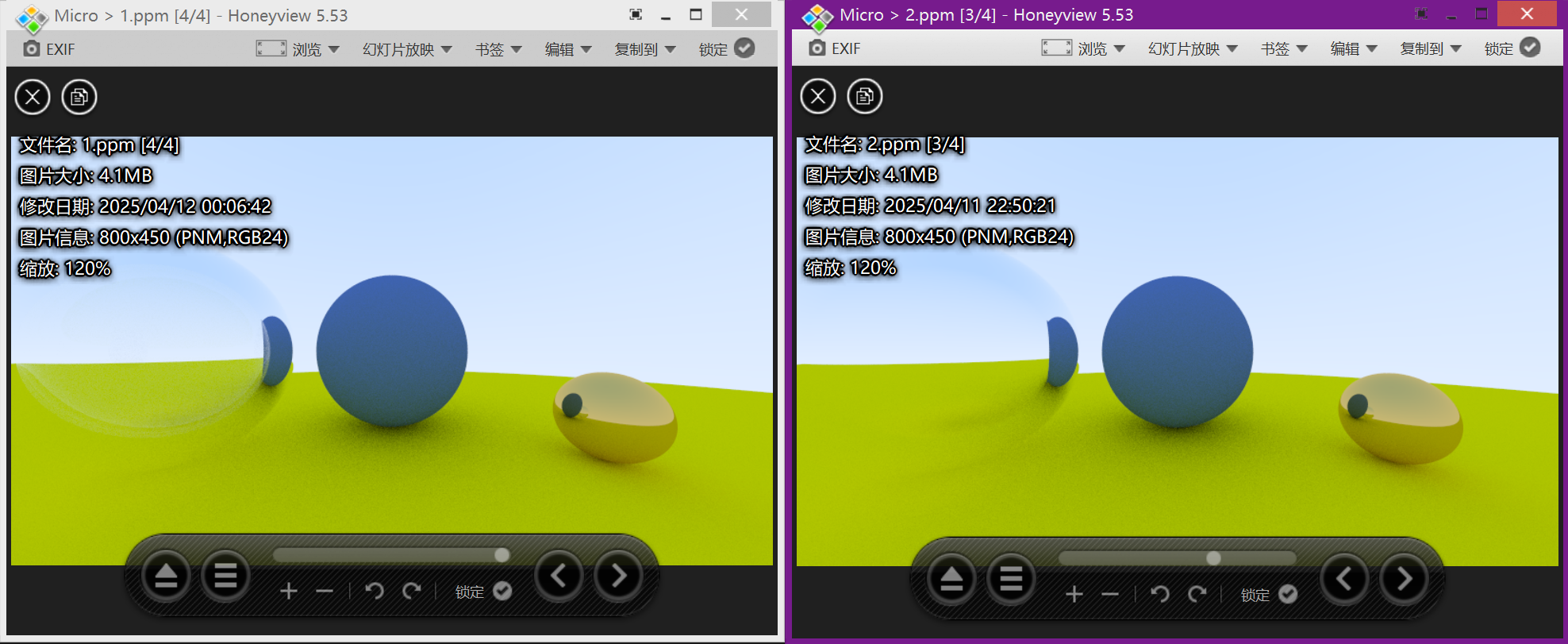image.png
左边确实更加逼真了。
建模一个空心玻璃球
我们建模一个空心玻璃球。这是一个由厚度的球体，里面有一个空气球。光线穿过这个物体，先击中外球，然后折射，然后穿过球内的空气。然后又击中球的内表面，折射，再击中外球的内表面，最后返回场景大气中。
我们设置外球，使用标准玻璃建模，折射率为1.50/1.00（从空气射入玻璃）。内球不同，内球使用空气建模，折射率设置为1.00/1.50（从玻璃射入空气）
我们设置一下main函数，再次渲染：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int main(){
...
auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto material_left = make_shared<dielectric>(1.50);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2),0.0);
auto material_bubble = make_shared<dielectric>(1.00/1.50);
world.add(make_shared<sphere>(point3( 0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3( 0.0, 0.0, -1.0), 0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3( 1.0, 0.0, -1.0), 0.5, material_right));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.4, material_bubble));
...
}
|
image.png
感觉不错啊，今天就到此为止吧