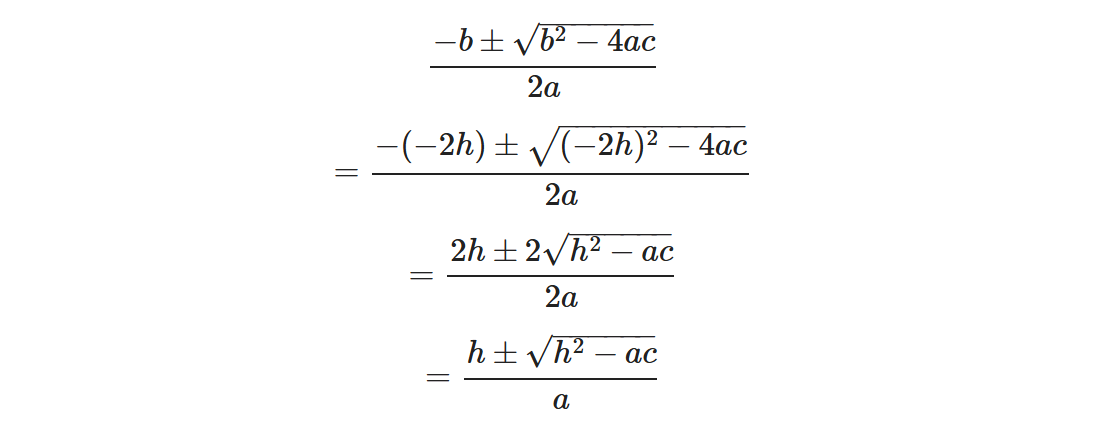Ylin's Blog
0%

32:初始图形学(5)

发表于 更新于 分类于 ，
本文字数： 2.8k 阅读时长 ≈ 10 分钟

感觉学的还是有点慢啊，刚刚往后看了一点，感觉后面的知识越来越难，我得赶快点学。

法向量和多物体处理

根据法向量进行表面着色

我们需要计算出表面法线进而进行着色。（法线是垂直于交点处的表面的向量）

法向量的计算使用决策有以下两种情况：

  • 法向量可以有任意长度，这些长度可以附带额外的信息，比如反射啥的
  • 法向量全部进行单位化，此时法向量仅仅代表其法线方向

我们可以看到法线的单位化过程中有开方操作，这个操作可能会花费较多的时间，但是我们仍然保留它，理由有三：

  • 你不应该等到要用的时候再进行单位化，设置条件可能会导致程序更加复杂
  • 我们会经常用到单位化的法向量
  • 法向量的单位化比想象中的简单，根据特定的几何类可以定制不同的单位化策略，如在球体中可以通过除以radius实现法向量的单位化

综上考虑，我们对所有的法向量都进行单位化。

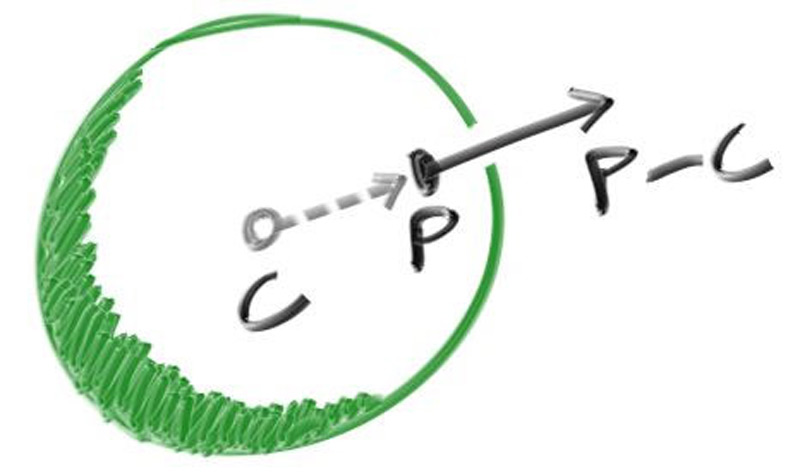
球体的外法线的计算方式也很简单：

1
2
vec(d) = point(P) - point(C)
unit(vec(d)) = vec(d)/radius
image.png

由于我们的单位向量的大小是1也就是说，单位法向量在其他任意方向的分量范围都在[-1,1]内，所以我们可以将其每个分量都映射到[0,1]的区间内，然后将（x,y,z）映射到 （red,green,blue）

我们需要计算出t从而计算出法向量的信息，我们确保球体是在摄像机的前方，所以不必考虑t的负值。当t有多个解的时候，我们只考虑离我们最近的交点（最小的t值），这样我们可以计算出我们的法向量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
double hit_sphere(const point3& center,double radius,const ray& r){
    vec3 oc = center - r.origin();
    auto a = dot(r.direction(),r.direction());
    auto b = -2.0 * dot(r.direction(),oc);
    auto c = dot(oc,oc) - radius*radius;
    auto discriminant = b*b - 4*a*c;
	//判断delta值，并计算t（这里计算的是较小的t）
    if(discriminant < 0.0){
        return -1.0;
    }else{
        return (-b - std::sqrt(discriminant)) / (2.0*a);
    }
}

color ray_color(ray & r){
    auto t = hit_sphere(point3(0,0,-1),0.5,r);
    //根据t的分量进行上色
    if(t > 0.0){
        vec3 N = unit_vector(r.at(t) - point3(0,0,-1));
        return 0.5*color(N.x()+1,N.y()+1,N.z()+1);
    }

    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y() + 1.0);
    return (1.0-a)*color(1.0,1.0,1.0) + a*color(0.5,0.7,1.0);
}

我们将程序修改后运行渲染得到了新的图片：

image.png

光线计算的简化

我们查看原本的交点计算方程：

1
2
3
4
5
6
7
8
9
10
11
12
13
double hit_sphere(const point3& center,double radius,const ray& r){
    vec3 oc = center - r.origin();
    auto a = dot(r.direction(),r.direction());
    auto b = -2.0 * dot(r.direction(),oc);
    auto c = dot(oc,oc) - radius*radius;
    auto discriminant = b*b - 4*a*c;

    if(discriminant < 0.0){
        return -1.0;
    }else{
        return (-b - std::sqrt(discriminant)) / (2.0*a);
    }
}

我们注意到b中有一个-2的因子，那么我们考虑将其分离出来，令b = -2h

于是方程可以进行以下变换实现简化：

image.png

同时我们知道向量的自己和自己的点积，等同于向量的平方dot(vec(v),vec(v)) = vec(v)^2

所以我们的程序可以改进成以下形式(没看出改进太多啊)：

1
2
3
4
5
6
7
8
9
10
11
12
13
double hit_sphere(const point3& center,double radius,const ray& r){
    vec3 oc = center - r.origin();
    auto a = r.direction().length_squared();
    auto h = dot(r.direction(),oc);
    auto c = oc.length_squared() - radius*radius;
    auto discriminant = h*h - a*c;

    if(discriminant < 0.0){
        return -1.0;
    }else{
        return (h - std::sqrt(discriminant)) / a;
    }
}

可被(光线)击中类的抽象

接下来我们需要考虑当有多个球体的情况，你可能觉得很简单，可以创建一个数组来实现，但实际上有更好的选择——创建一个抽象类，这里我们称其为hittable类。

这个抽象类将接受ray作为参数。同时我们添加一个有效的命中区间（t_min到t_max），这样便于我们对t的计算，只有在有效命中区内，t才被采用，命中才计数。同时我们还要考虑一个问题，那就是我们只需要考虑并计算离我们较近的东西的法线，所以我们需要采取一些方案来计算他们，以下是一个抽象类。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#ifndef RENDER_C___HITTABLE_H
#define RENDER_C___HITTABLE_H

#include "ray.h"

//用于存储光线与物体相交的重要信息
class hit_record{
public:
    point3 p;
    vec3 normal;
    double t;
};

class hittable{
public:
    virtual ~hittable() = default;
    //纯虚函数，用来实现函数的多态性
    virtual bool hit(const ray& r, double ray_min,double ray_max,hit_record& rec) const = 0;
};

#endif //RENDER_C___HITTABLE_H

在此基础上实现一个球体的类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#ifndef RENDER_C___SPHERE_H
#define RENDER_C___SPHERE_H

#include "vec3.h"
#include "hittable.h"

class sphere: public hittable{
public:
    sphere(const point3& center, double radius) : center(center), radius(std::fmax(0,radius)) {}
	//fmax返回两个浮点数参数较大的一个，fmin同理
    bool hit(const ray& r, double ray_min,double ray_max,hit_record& rec) const override{
        vec3 oc = center - r.origin();						// override 重写基类的虚函数
        auto a = r.direction().length_squared();
        auto h = dot(r.direction(),oc);
        auto c = oc.length_squared() - radius*radius;

        auto discriminant = h*h - a*c;
        if(discriminant < 0.0){
            return false;
        }

        //解t并进行判断
        auto sqrtd = std::sqrt(discriminant);
        auto root = (h - sqrtd) / a;
        if(root <= ray_min || ray_max <= root){
            root = (h + sqrtd) / a;
            if(root <= ray_min || ray_max <= root)
                return false;
        }
        
        rec.t = root;
        rec.p = r.at(rec.t);
        rec.normal = (rec.p - center) / radius;
        
        return true;
    }
    
private:
    point3 center;
    double radius;
};


#endif //RENDER_C___SPHERE_H

前表面与后表面

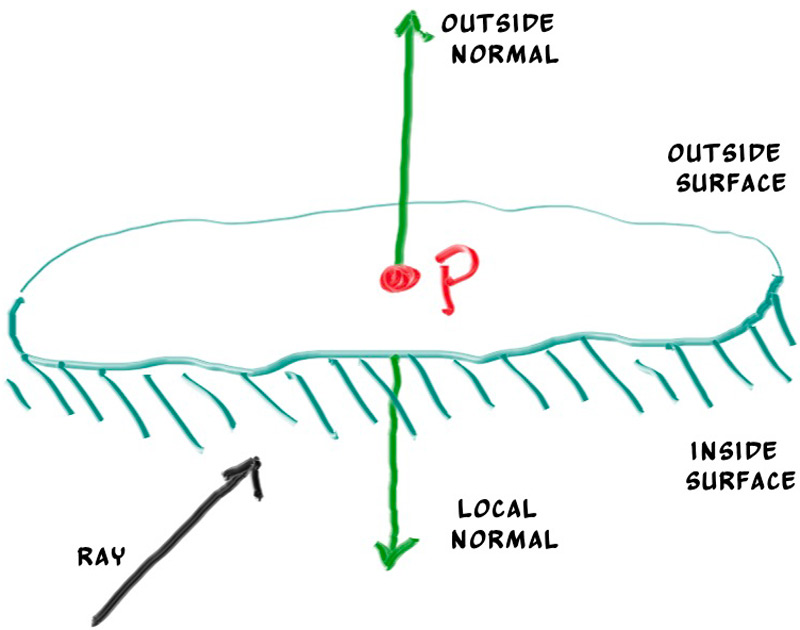
我们先前提到了关于法线的几个决策，现在我们需要决定法线是否应该始终指向外面。当然，我们可以利用法线始终指向外面的方式来进行光线来向的判断，并帮助我们区分前后表面。

image.png

以这张图为例，我们可以通过计算光线方向和法线（始终朝外）的点积，并判断它的正负来实现其方向的判断。如果其点积为正，说明光线与法线同向，照射到的是内表面。如果点积为负，说明光线与法线反向，照射到的是外表面。我们可以通过以下程序实现判断：

1
2
3
4
5
6
7
8
9
10
bool front_face;
if(dot(ray_direction,outward_normal) > 0.0){
    // 光线在球体内部
    normal = -outward_normal;	//实际的法线方向，需要翻转
    front_face = false;
}else{
    // 光线在球体外部
    normal = outward_normal;
    front_face = true;
}

我们将其添加到我们的hittable.h和sphere中：

1
2
3
4
5
6
7
8
9
10
11
12
13
class hit_record{
public:
    point3 p;
    vec3 normal;
    double t;
    bool front_face;

    void set_face_normal(const ray& r,const vec3& outward_normal){
        //设置交点的法线方向
        front_face = dot(r.direction(),outward_normal) < 0;
        normal = front_face ? outward_normal : -outward_normal;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class sphere : public hittable {
  public:
    ...
    bool hit(const ray& r, double ray_tmin, double ray_tmax, hit_record& rec) const {
        ...

        rec.t = root;
        rec.p = r.at(rec.t);
        vec3 outward_normal = (rec.p - center) / radius;
        rec.set_face_normal(r, outward_normal);

        return true;
    }
    ...
};

可击中对象的列表

我们之前创建了一个抽象类hittabel.h，用来描述光线可以相交的物体。现在我们再创建一个类来存储具有hittable特性的列表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#ifndef RENDER_C___HITTABLE_LIST_H
#define RENDER_C___HITTABLE_LIST_H

#include "hittable.h"

#include <memory>
#include <vector>

using std::make_shared;
using std::shared_ptr;

class hittable_list : public hittable {
public:
    std::vector<shared_ptr<hittable>> objects;
	// 创建了一个可击中对象的数组
    hittable_list(){}
    hittable_list(shared_ptr<hittable> object) {add(object);}

    void clear() {objects.clear();}

    void add(shared_ptr<hittable> object) {
        objects.push_back(object);
    }

    bool hit(const ray& r, double ray_tmin, double ray_tmax, hit_record& rec) const override{
        hit_record temp_rec;
        bool hit_anything = false;
        auto closest_so_far = ray_tmax;

        for(const auto& object : objects){
            if(object->hit(r,ray_tmin,closest_so_far,temp_rec)){
                hit_anything = true;
                closest_so_far = temp_rec.t;
                rec = temp_rec;
            }
        }
        return hit_anything;
    }
};

#endif //RENDER_C___HITTABLE_LIST_H

这里有些地方用到了C++的一些特性，需要特别强调一下。

shared_ptr<> 是一个智能指针，被包含在<memory>中，用来指向已经分配的类型，它可以自动管理内存，当对象不再被任何shared_ptr引用时，自动释放内存。我们可以使用make_shared<thing>(...)为数据类型thing创建一个实例，并返回一个shared_ptr<thing>例如：

1
2
3
auto double_ptr = make_shared<double>(0.41);
auto vec3_ptr = make_shared<vec3>(1.1,1.2,1.3);
auto sphere_ptr = make_shared<sphere>(point3(0,0,0),1.0)

还有一个需要注意的用到的特性是std::vector,其被包含在<vector>中，其用来生成一个动态数组，并且支持对其集合仅从指定的操作。例如：

1
2
3
4
5
6
7
8
9
std::vector<shared_ptr<hittable>> objects;
//添加一个值
objects.push_back(object);
//删除所有值
objects.clear();
//数组大小
objects.size();
//访问
objects[]

大概涉及到这些吧，剩下的之后再慢慢了解

常用常量和实用函数

我们设置一个头文件，我们放置一些常用的数学常量和一些常用的头文件，这样方便我们的调取

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#ifndef RENDER_C___RTWEEKEND_H
#define RENDER_C___RTWEEKEND_H

#include <cmath>
#include <iostream>
#include <limits>
#include <memory>

using std::make_shared;
using std::shared_ptr;

//常量设置
const double infinity = std::numeric_limits<double>::infinity();
const double pi = 3.1415926535897932385;

//实用函数
inline double degree_to_radius(double degrees){
    return degrees * pi / 180.0;
}

//常用文件头
#include "color.h"
#include "ray.h"
#include "vec3.h"

#endif //RENDER_C___RTWEEKEND_H

现在我们的rtweekend.h里面已经包含了大多数常用的文件头，

我们现在利用上述新创建文件头，写一个新的main函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
//这里我们修改了一下头文件还有ray_color函数
#include "rtweekend.h"
#include "hittable.h"
#include "hittable_list.h"
#include "sphere.h"

#include <iostream>

color ray_color(ray & r,const hittable& world){
    hit_record rec;
    if(world.hit(r,0,infinity,rec)){		//只有t在(0,+无穷)的时候才成立
        return 0.5*(rec.normal + color(1,1,1));
    }

    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y()+1.0);
    return (1.0 - a)*color(1.0,1.0,1.0) + a*color(0.5,0.7,1.0);
}

int main(){
    auto aspect_radio = 16.0/9.0;	//长宽比
    int image_width = 400;

    //计算图像的高度，并确保图像的高度至少为1（单位长度）
    int image_height = int (image_width / aspect_radio);
    image_height = (image_height < 1) ? 1 : image_height;

    //球体列表
    hittable_list world;

    world.add(make_shared<sphere>(point3(0,0,-1),0.5));
    world.add(make_shared<sphere>(point3(0,-100.5,-1),100));

    //确保视口的宽高比和图像的宽高比一样
    auto focal_length = 1.0;
    auto viewport_height = 2.0;
    auto viewport_width = viewport_height * (double(image_width)/image_height);
    auto camera_center = point3(0,0,0);

    //设置视口向量与单位长度
    auto viewport_u = vec3(viewport_width,0,0);
    auto viewport_v = vec3(0,-viewport_height,0);
    auto pixel_delta_u = viewport_u/image_width;
    auto pixel_delta_v = viewport_v/image_height;

    //计算像素点位
    auto viewport_upper_left = camera_center - vec3(0,0,focal_length) - viewport_v/2 - viewport_u/2;
    auto pixel00_loc = viewport_upper_left + 0.5*(pixel_delta_u+pixel_delta_v);


    //渲染器
    std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";
    for(int j=0;j<image_height;j++){
        std::clog << "\rScanlines remaining: " << (image_height - j) << ' ' << std::flush;
        for(int i=0;i<image_width;i++){
            auto pixel_center = pixel00_loc + (i*pixel_delta_u) + (j*pixel_delta_v);
            auto ray_direction = pixel_center - camera_center;
            ray r(camera_center,ray_direction);

            color pixel_color = ray_color(r,world);
            write_color(std::cout,pixel_color);
        }
    }
    std::clog << "\rDone.                   \n";
}

这个是我们渲染出来的新图片，我们设置了一个大的球体在下面作为一个地面。

image.png

区间类

我们在判断是否击中的hit()函数中我们经常设置一个区间(tmin,tmax)，为了方便之后的使用，我们将这个区间类给抽象出来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#ifndef RENDER_C___INTERVAL_H
#define RENDER_C___INTERVAL_H

#include "rtweekend.h"

class interval{
public:
    double min,max;
    //默认区间是空的
    interval() : min(+infinity),max(-infinity) {}

    interval(double min,double max): min(min),max(max) {}

    double size() const{
        return max - min;
    }
    //闭区间
    bool contains(double x) const {
        return min <= x && x <= max;
    }
    //开区间
    bool surrounds(double x) const{
        return min < x && x < max;
    }

    static const interval empty,universe;
};

const interval interval::empty = interval(+infinity,-infinity);
const interval interval::universe = interval(-infinity,+infinity);

#endif //RENDER_C___INTERVAL_H

我们现在可以用这个头文件去更新之前用到了区间的程序

1
2
3
4
5
6
//hittable.h
class hittable {
  public:
    ...
    virtual bool hit(const ray& r, interval ray_t, hit_record& rec) const = 0;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//hittable_list.h
class hittable_list : public hittable {
  public:
    ...
    bool hit(const ray& r, interval ray_t, hit_record& rec) const override {
        hit_record temp_rec;
        bool hit_anything = false;
        auto closest_so_far = ray_t.max;

        for (const auto& object : objects) {
            if (object->hit(r, interval(ray_t.min, closest_so_far), temp_rec)) {
                hit_anything = true;
                closest_so_far = temp_rec.t;
                rec = temp_rec;
            }
        }

        return hit_anything;
    }
    ...
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//sphere.h
class sphere : public hittable {
  public:
    ...
    bool hit(const ray& r, interval ray_t, hit_record& rec) const override {
        ...

        auto root = (h - sqrtd) / a;
        if (!ray_t.surrounds(root)) {
            root = (h + sqrtd) / a;
            if (!ray_t.surrounds(root))
                return false;
        }
        ...
    }
    ...
};
1
2
3
4
5
6
7
8
9
10
color ray_color(const ray& r, const hittable& world) {
    hit_record rec;
    if (world.hit(r, interval(0, infinity), rec)) {
        return 0.5 * (rec.normal + color(1,1,1));
    }

    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y() + 1.0);
    return (1.0-a)*color(1.0, 1.0, 1.0) + a*color(0.5, 0.7, 1.0);
}

以上就是需要更新的地方啦

这一篇的内容比较多，写了差不多两天，得好好消化一下啦。