学到一半区研究旋转立方体去了，确实好玩，受益匪浅啊，刚好搞明白了上一章相机的设置和视图的投影，现在继续学习。

添加一个球

我们现在向我们的光线追踪器中添加一个物体。我们从添加一个球体开始（因为它是最容易分析实现的）

射线-球面的交汇

这一部分将有大量的公式，但是我现在还没有搞明白Latex的渲染问题（这个太麻烦了，我已经试过几次了），可能会用比较丑陋方式来表达或者直接上截图

我们知道球体的表达式：

1	x^2 + y^2 + z^2 = r^2

当球心为C(C_x,C_y,C_z)时，我们有：

1	(C_x - x)^2 + (C_y - y)^2 + (C_z - z)^2 = r^2

但是这个是数值上的运算，我们需要想办法将它转换成向量vec3的形式，这里观察可得，实际上我们可以用一点P(x,y,z)来表示球体上的任意一点，也就是说从CP向量，可以用point(C)-point(P)来表示，现在我们可以用向量的概念去理解这个式子：

1	(point(C)-point(P))*(point(C)-point(P)) = (C_x - x)^2 + (C_y - y)^2 + (C_z - z)^2 = r^2

现在将射线的路径和球体的方程式联立起来：

P(t) = Q + td
(point(C)-point(P))*(point(C)-point(P)) = r^2

联立得：

t^2*vec(d)*vec(d) - 2*t*(point(C)-point(Q)) + (point(C)-point(Q))*(point(C)-point(Q)) - r^2 = 0

这是一个关于t的一元二次方程，我们可以根据医院二次方程的求解方程式来计算t，并得到射线与球体的相交情况(注意以下的乘法都是点乘)：

求解方程式：
x = (-b +- sqrt(b^2 - 4*a*c))/(2*a)
根据联立方程式得到的数值：
a = vec(d)*vec(d)
b = -2*vec(d)*(point(C)-point(Q))
c = (point(C)-point(Q))*(point(C)-point(Q)) - r^2

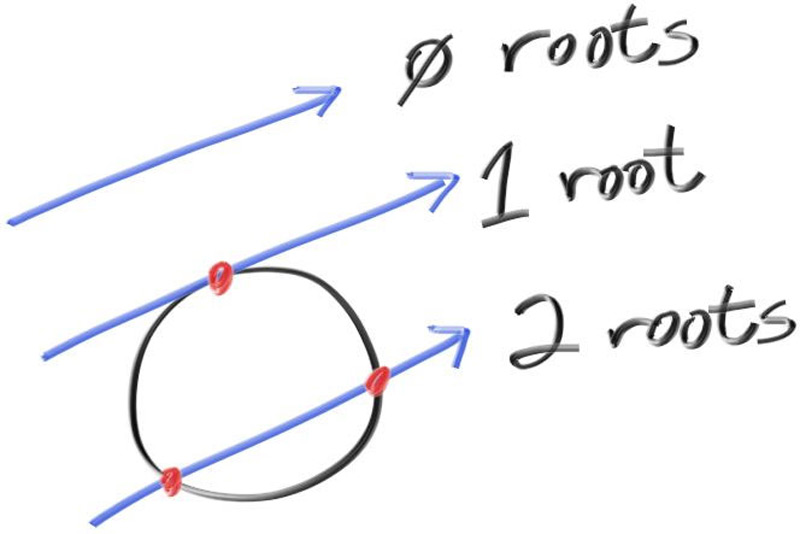
带入以上的数据就可以解出t，同时可以判断光线与球体的相交情况

创建一个带有小球的光追图像

我们现在将刚刚计算得到的数学公式硬编码进入我们的程序，并设置球体的中心在（0，0，-1）,半径为0.5

bool hit_sphere(const point3& center,double radius,const ray& r){
    vec3 oc = center - r.origin();		//计算(point(C)-point(Q))
    auto a = dot(r.direction(),r.direction());
    auto b = -2.0 * dot(r.direction(),oc);
    auto c = dot(oc,oc) - radius*radius;
    auto discriminant = b*b - 4*a*c;
    return (discriminant >= 0);
}

color ray_color(ray & r){
    if(hit_sphere(point3(0,0,-1),0.5,r))
        return {1,0,0};

    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y() + 1.0);
    return (1.0-a)*color(1.0,1.0,1.0) + a*color(0.5,0.7,1.0);
}

我们将这一部分添加进入先前的代码可以得到我们渲染出来的图像，中间的红色是我们添加的球体。

不过此时程序仍然存在一个问题，我们并不能区分摄像机前后的物体，由于射线的对称性，当球体位于(0,0,1)的时候，存在t的解为负数，导致渲染出相同的图片。

同时，我们现在还不能对物体进行前后的判断，还有阴影，反射光线等功能还有多个物体的共存，我们在接下来的学习中，慢慢尝试解决这个问题，今天就到此为止啦。

Ylin's Blog

31:初始图形学(4)

添加一个球

射线-球面的交汇

创建一个带有小球的光追图像