Ylin's Blog
0%

30:旋转立方体

发表于 更新于 分类于

看到一个视频，对其内容比较感兴趣，刚好今天没什么事，我们来深入解析一下这个项目

视频链接：终端字符旋转立方体

参考链接：Donut math: how donut.c works

这是我们最终想要实现的效果（一个旋转的立方体）：

image.png

旋转

怎么让一个立方体转起来，我们是怎么实现的？实际上这里用到的是线性代数的几何原理。

这里直接给出实现方法，通过三个旋转矩阵对向量进行三次线性变换，从而实现对点的旋转效果：

  • 我们以正方体的几何中心作为原点，此时正方体表面的任意一点可被表示为向量(i, j, k)
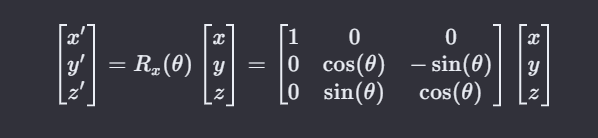
  • 现在使用通过绕X轴旋转的旋转矩阵，来实现变换image.png
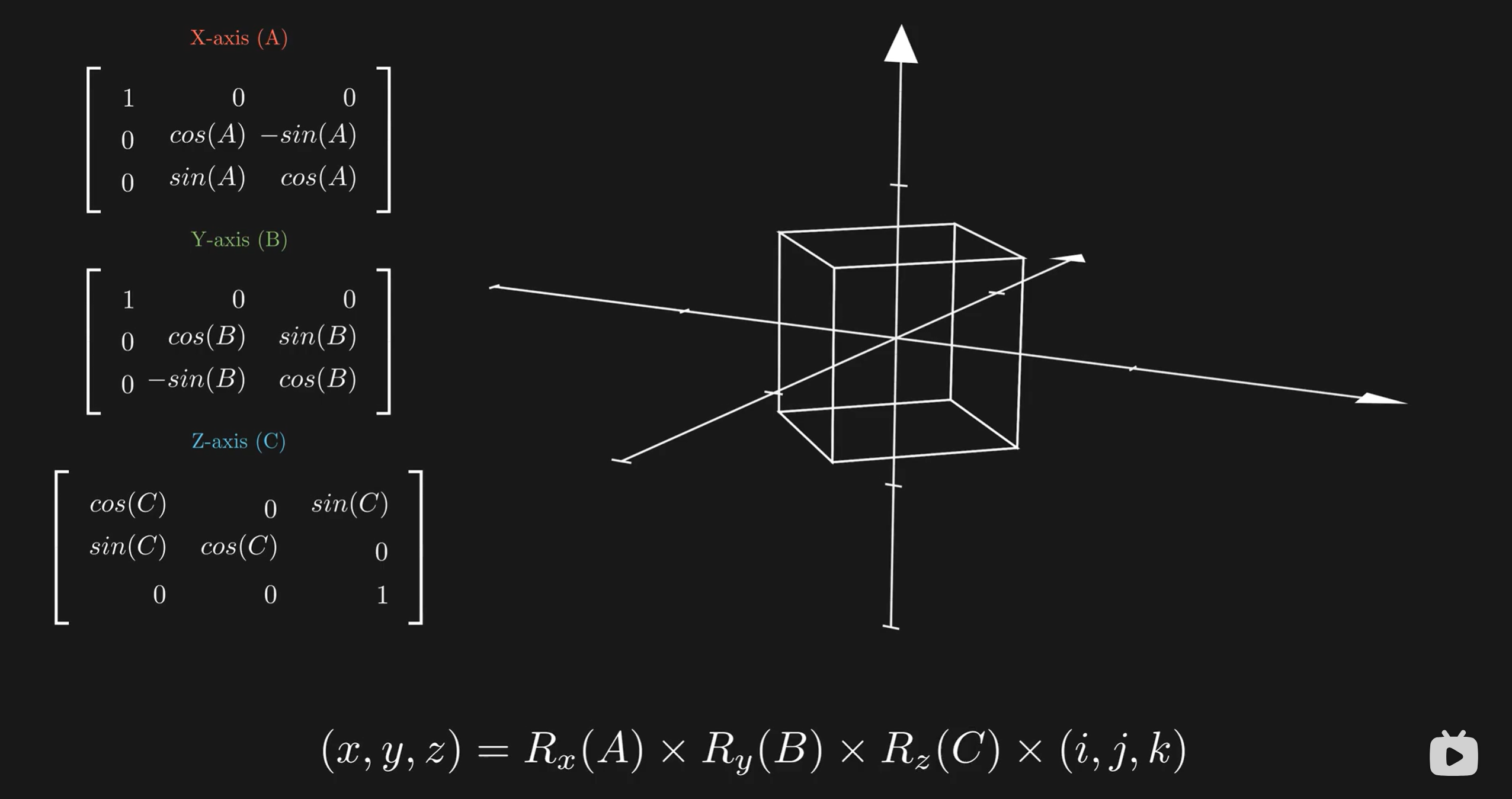
  • 想要对于Y轴和Z轴的旋转的话，乘以对应的旋转矩阵即可实现image.png

这样我们就通过矩阵乘法实现了向量旋转的效果，我们可以得到旋转后的点的位置

这里我们使用wiki百科中的内旋矩阵来实现我们的计算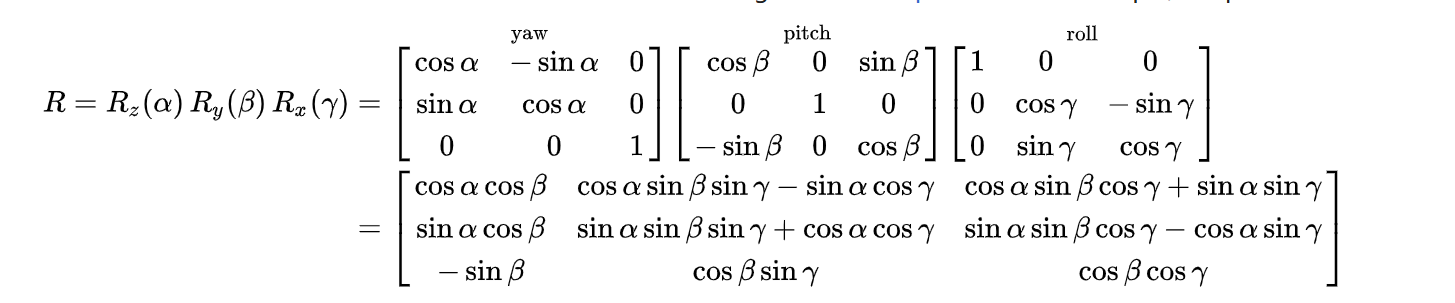image.png

接下来我们可以写出以下代码来计算我们的在任意时刻的点位：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
double A,B,C;
float calculateX(int i,int j,int k){
    return i*cos(A)cos(B) + 
        j*cos(A)*sin(B)*sin(C) - j*sin(A)*cos(C) +
        k*cos(A)*sin(B)*cos(C) + k*sin(A)*sin(C);
}
float calculateY(int i,int j,int k){
    return i*sin(A)*cos(B) +
        j*sin(A)*sin(B)*sin(C) + j*cos(A)*cos(C) +
        k*sin(A)*sin(B)*cos(C) - k*cos(A)*sin(C); 
}
float calculteZ(int i,int j,int k){
    return -i*sin(B) +
        j*cos(B)*sin(C) + 
        k*cos(B)*cos(C);
}

现在我们对立方体的模拟已经完成了，接下来我们需要想办法将其投影到我们的视图上面。

投影

我们根据这张图来进行解释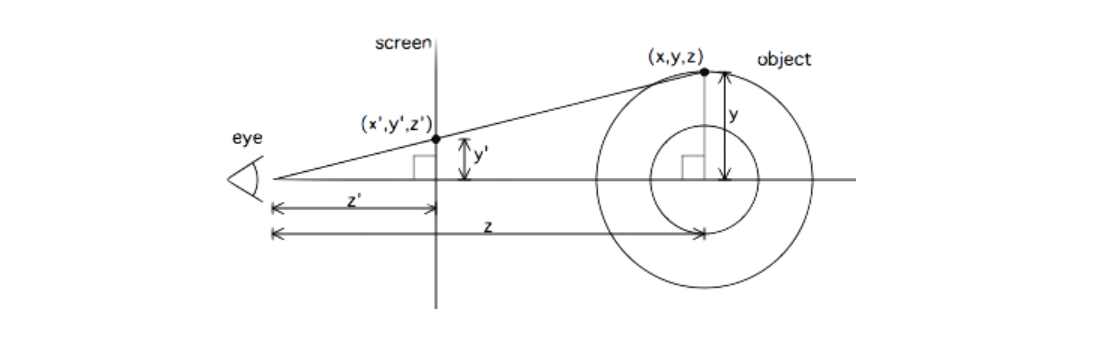image.png

这个object就是我们模拟出来的物体，也就是我们的正方体。screen是我们的屏幕，我们现在根据投影将物体投射在我们的屏幕上呈现出我们看到的效果。

这里可以看到得到等式关系y/z = y0/z0也就是说y0 = y*(z0/z)其中z0的值是保持不变的，我们将其设置为K1。我们就可以用等式xp = K1*ooz*x*2;yp = K1*ooz*y来表示它的坐标（这里xp需要乘2是因为终端中的字符有一定的长宽比，如果不乘以2，则投影出来的效果会比较窄）。

所以我们就可以写出我们的投影函数了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 变量
int idx;
int xp,yp;
float ooz;
float cubeWidth = 16;	//正方体大小
int width = 160,height = 44;	//视口大小
int distanceFromCamera = 60;	//视口距离物体几何中心的距离
int K1 = 40;				   //相机到视口的距离
float zbuffer[160*44];
char buffer[160*44];

void calculateForSurface(float cubeX,float cubeY,float cubeZ,char ch){
    //原点（0，0，0）实际上是相机的位置（即视点）
    x = calculateX(cubeX,cubeY,cubeZ);
    y = calculateY(cubeX,cubeY,cubeZ);
    z = calculateZ(cubeX,cubeY,cubeZ) + distanceFromCamera;

    ooz = 1/z; //one over zero
    xp = (int)(width/2 + K1*ooz*x*2);//这里乘2平衡字符的宽高比
    yp = (int)(height/2 + K1*ooz*y);

    idx = xp + yp*width;	//计算在数列中的位置
    if(idx >= 0 && idx < width*height){
        // z缓冲
        if(ooz > zbuffer[idx]){
            zbuffer[idx] = ooz;
            buffer[idx] = ch;
        }
    }
}

以上就是我们的投影函数了，你可能会注意到这一部分：

1
2
3
4
if(ooz > zbuffer[idx]){
    zbuffer[idx] = ooz;
    buffer[idx] = ch;
}

这就是大名鼎鼎的Z缓冲技术（Z-buffering），如果没有这个程序可能我们投影出来的效果就会是透视的，我们看物体的前面却能看到物体的背面，这是因为后面的字符覆盖到了前面的字符。所以在这里我们需要对每个点进行深度检测，即计算他们的ooz，如果z越大说明离得越远，反之则说明离得近。每次进行缓冲区的覆写之前我们都先对其做一次判断，如果当前Z的深度大于先前的点，则忽略。

这样的设计确保只有最近的表面可见，避免远处的物体错误的覆盖近处的物体。

展示

现在我们已经完成了我们的模拟函数和渲染和函数，接下来就需要进行一系列的初始化，让正方体动起来

我们直接将main函数给出，然后进行解释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
float zbuffer[160*44];
char buffer[160*44];
int backgroundASCIIcode = ' ';
float increamentSpeed = 0.5;
int main(){
    printf("\x1b[2j");		//cls的转义序列，用于清屏
    while(1){
        memset(buffer,backgroundASCIIcode,width*height);//设置背景为' '
        memset(zbuffer,0,width*height*4);			   //设置深度为无限深度
        for(float cubeX = -cubeWidth;cubeX < cubeWidth;cubeX+=increamentSpeed){
            for(float cubeY = -cubeWidth;cubeY < cubeWidth;cubeY+=increamentSpeed){
                calculateForSurface(cubeX,cubeY,-cubeWidth,'o');
                calculateForSurface(cubeWidth,cubeY,cubeX,'.');
                calculateForSurface(-cubeWidth,cubeY,-cubeX,'@');
                calculateForSurface(-cubeX,cubeY,cubeWidth,'^');
                calculateForSurface(cubeX,-cubeWidth,-cubeY,'+');
                calculateForSurface(cubeX,cubeWidth,cubeY,'-');
            }
        }	
        printf("\x1b[H");	//将光标置于左上角的转义序列，确保打印的视图稳定完整
        printf("\x1b[?25l");//隐藏光标的转义序列，保证观看的优美
        fflush(stdout);
        //用于打印缓冲图像，并且用三元运算符号判断换行时机
        for(int k=0 ;k< width*height;k++){
            putchar(k%width ?buffer[k] : 10);
        }
        //设置转动
        A += 0.04;
        B += 0.04;
        C += 0.04;
        usleep(8000);
    }
}

你可能会对这一部分代码感到困惑：

1
2
3
4
5
6
7
8
9
10
for(float cubeX = -cubeWidth;cubeX < cubeWidth;cubeX+=increamentSpeed){
            for(float cubeY = -cubeWidth;cubeY < cubeWidth;cubeY+=increamentSpeed){
                calculateForSurface(cubeX,cubeY,-cubeWidth,'o');
                calculateForSurface(cubeWidth,cubeY,cubeX,'.');
                calculateForSurface(-cubeWidth,cubeY,-cubeX,'@');
                calculateForSurface(-cubeX,cubeY,cubeWidth,'^');
                calculateForSurface(cubeX,-cubeWidth,-cubeY,'+');
                calculateForSurface(cubeX,cubeWidth,cubeY,'-');
            }
        }

实际上这是对正方体的初始化，和对其点位的跟踪计算，我们将正方体的几何中心视作原点（0，0，0），那么根据这个原点建系。Z轴指向垂直向内，Y轴指向竖直向上，X轴指向水平向右。那么我们就可以确定正方形六个面的位置了：

面 固定坐标 变化的坐标 几何意义
前面 Z = -10 X 和 Y 靠近屏幕的面（Z最小）
后面 Z = +10 X 和 Y 远离屏幕的面（Z最大）
右面 X = +10 Y 和 Z 立方体右侧的面（X最大）
左面 X = -10 Y 和 Z 立方体左侧的面（X最小）
顶面 Y = +10 X 和 Z 立方体顶部的面（Y最大）
底面 Y = -10 X 和 Z 立方体底部的面（Y最小）

至于CubeX和CubeY的值则是用来确定位置，以确保方向一定。

这么解释理解起来比较麻烦，实际上你仍然可以理解成一个矩阵变换的过程：

  • 我们设当前面上一点的位置为(x,y,z)
  • 那么右面上的点的表示即为，绕Y轴旋转90度的旋转矩阵的线性变换
  • 其他五个面同理，我们可以得到以下的线性关系：
面 面上一点的表示
前面 （x,y,z）
后面 （-x,y,-z）
右面 （-z,y,x）
左面 （z,y,-x）
顶面 （x,z,-y）
底面 （-x,z,y）

然后依次进行计算即可，简而言之这是一个将正方体内的坐标系转换到3D世界中的坐标系的一个过程

至此我们的程序就完成了,效果见下图：

image.png

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<stdio.h>
#include<math.h>
#include<unistd.h>

int idx;
int xp,yp;
float ooz;
float x,y,z;
double A,B,C;
float cubeWidth = 16;
int width = 160,height = 44;
int distanceFromCamera = 60;
int K1 = 40;
float zbuffer[160*44];
char buffer[160*44];
int backgroundASCIIcode = ' ';
float increamentSpeed = 0.5;

float calculateX(float i,float j,float k){
    return i*cos(A)*cos(B) +
           j*cos(A)*sin(B)*sin(C) - j*sin(A)*cos(C) +
           k*cos(A)*sin(B)*cos(C) + k*sin(A)*sin(C);
}
float calculateY(float i,float j,float k){
    return i*sin(A)*cos(B) +
           j*sin(A)*sin(B)*sin(C) + j*cos(A)*cos(C) +
           k*sin(A)*sin(B)*cos(C) - k*cos(A)*sin(C);
}
float calculateZ(float i,float j,float k){
    return -i*sin(B) +
           j*cos(B)*sin(C) +
           k*cos(B)*cos(C);
}
void calculateForSurface(float cubeX,float cubeY,float cubeZ,char ch){
    x = calculateX(cubeX,cubeY,cubeZ);
    y = calculateY(cubeX,cubeY,cubeZ);
    z = calculateZ(cubeX,cubeY,cubeZ) + distanceFromCamera;

    ooz = 1/z;
    xp = (int)(width/2 + K1*ooz*x*2);
    yp = (int)(height/2 + K1*ooz*y);

    idx = xp + yp*width;
    if(idx >= 0 && idx < width*height){
        if(ooz > zbuffer[idx]){
            zbuffer[idx] = ooz;
            buffer[idx] = ch;
        }
    }
}


int main(){
    printf("\x1b[2j");
    while(1){
        memset(buffer,backgroundASCIIcode,width*height);
        memset(zbuffer,0,width*height*4);
        for(float cubeX = -cubeWidth;cubeX < cubeWidth;cubeX+=increamentSpeed){
            for(float cubeY = -cubeWidth;cubeY < cubeWidth;cubeY+=increamentSpeed){
                calculateForSurface(cubeX,cubeY,-cubeWidth,'o');
                calculateForSurface(cubeWidth,cubeY,cubeX,'.');
                calculateForSurface(-cubeWidth,cubeY,-cubeX,'@');
                calculateForSurface(-cubeX,cubeY,cubeWidth,'^');
                calculateForSurface(cubeX,-cubeWidth,-cubeY,'+');
                calculateForSurface(cubeX,cubeWidth,cubeY,'-');
            }
        }
        printf("\x1b[H");
        printf("\x1b[?25l");
        fflush(stdout);
        for(int k=0 ;k< width*height;k++){
            putchar(k%width ?buffer[k] : 10);
        }
        A += 0.04;
        B += 0.04;
        C += 0.04;
        usleep(8000);
    }
}