Ylin's Blog
0%

21:KMP算法精读

发表于 更新于 分类于

这是第二遍学KMP算法，第一遍学习的过程中，对他的原理理解的是云里雾里。现在回过头来，深度学习一下KMP算法

首先我们要清楚什么是KMP算法？

KMP

KMP算法的优点相较于暴力匹配算法(BF)更有效率。这是因为KMP算法会利用每次匹配得到的已有的信息，来进行回溯。从而开始一次新的匹配。而暴力算法由于重复的匹配，其复杂度为 O(m*n)；KMP算法的主串指针始终向前，所以复杂度为 O(m+n)

next数组

我看很多教程一开始都是先讲KMP算法的实现，只是提了一嘴next数组的大致内容，我觉得挺难懂的。所以这里先从next数组开始讲起：

要讲next数组，我们首先要从字符串的最大公共前后缀讲起，下面的图片很好的体现了这个概念。每次增大子串的长度，然后求得其对应的最大公共前后缀长度。

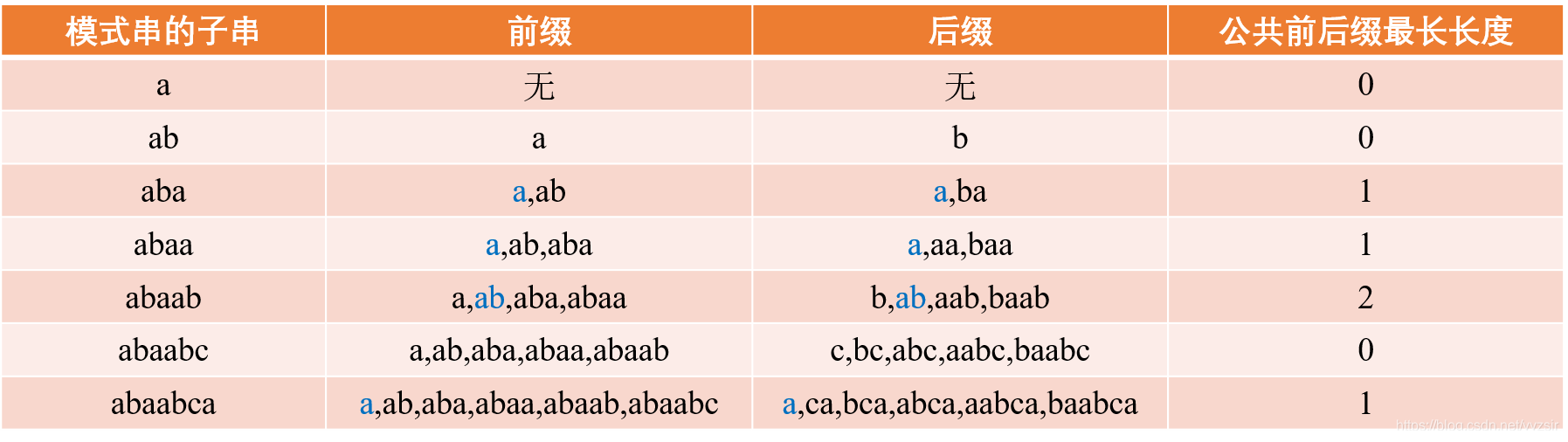
image.png

在求的子串的最大公共前后缀组后，我们便可以着手开始建立我们的next数组。

（1）首先我们需要明确next数组在这里的作用是什么？

当模式串的某个字符与主串的某个字符失配时，我们需要根据失配的位置 j,还有我们的 next数组，来确定下一次模式串开始匹配的位置。下一步用 next[j]处的字符继续与主串 i处的字符进行匹配。相当于将模式串向右移动了 j-next[j]的长度

（2）接下来的难点在于如何构建next数组

首先我们让 next[0] = -1作为一个标记，且我们容易得到 next[1] = 0，那么在此基础之上，我们需要结合现有的信息来递推下一个 next[j+1]的值。现在问题转换成了，如何利用已有信息，求下一个 next[j+1]的值？

对此我们需要分成两种情况进行判断：

  • 当p_k = p_j时，next[j+1] = next[j] + 1 = k+1,代表该字符前有最大长度为k+1的最大公共前后缀
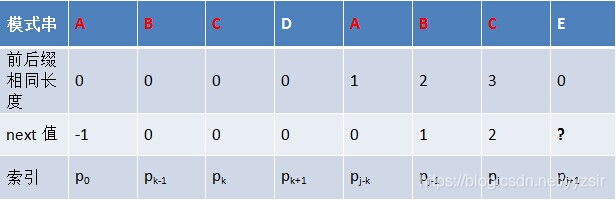
image.png
  • 当p_k != p_j时，我们就需要寻找更短的最大公共前后缀，此时关键来了，怎么找寻更短的最大公共前缀？
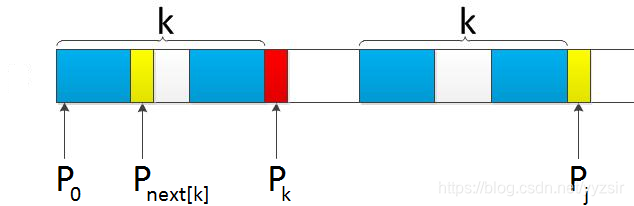
image.png

​ 因为 P_k!=P_j，所以我们需要再次尝试 P_next[k]和 P_j的比较，如此一直递归下去。直到得到 P_next[next[...]]和 P_j相 等，从而令 next[j+1] = next[index[P_next[…]]] + 1 = k+1；或者始终不能成功配对，则令 next[j+1] = 0

现在我们可以写出next数组的递推算法：

1
2
3
4
5
6
7
8
9
10
11
12
void GetNext(char T[]){
    int j=0,k=-1;
    next[j] = k;
    while (T[j]!='\0'){
        if(k==-1||T[j]==T[k]){
            j++;
            k++;
            next[j]=k;
        }
        else k=next[k];
    }
}

这个程序还有一个递归版本：

1
2
3
4
5
6
7
8
9
10
11
12
int GetNext(int j,char T[]){
    if(j==0)return -1;
    if(j>0){
        int k = GetNext(j-1,T);
        while(k>=0){
            if(T[j-1]==T[k])return k+1;
            else k=GetNext(k,T);
        }
        return 0;
    }
    return 0;
}

KMP算法

我们在得到next数组之后，便可以根据next数组的特性和简单的判断，来实现我们的KMP算法，以下是我们的算法流程：

  • 如果j = -1，则i++，j++，继续匹配下一个字符
  • 如果S[i] = T[j]，则i++，j++，继续匹配下一个字符
  • 如果j != -1，且S[i] != P[j]，则i不变，j = next[j]。这意味着失配，接下来模式串需要对主串相对右移j-next[j]的距离

现在我们可以写出完整的KMP算法：

1
2
3
4
5
6
7
8
9
10
11
12
int KMP(int start,char S[],char T[]){
    int i = start,j = 0;
    while(S[i]!='\0'&&T[j]!='\0'){
        if(j==-1||S[i]==T[j]){
            i++;		//下一个字符的比较
            j++;		//模式串右移
        }
        else j = next[j];
    }
    if(T[j]=='\0') return(i-j);		//匹配成功则返回下标（当前比较位-比较长度 = 起始下标）
    else return -1;
}

当然，在KMP的基础之上，还有很多优化之后的算法，在此就不过多赘述

Python版本

这个是python版本的KMP算法，基本上一样，只不过边界条件的判断改为使用长度判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution(object):
    def strStr(self, haystack:str, needle:str)->int:
        next = self.getnext(needle)
        h,n = 0,0
        while h<len(haystack) and n<len(needle):
            if n==-1 or haystack[h] == needle[n]:
                h += 1
                n += 1
            else:
                n = next[n]
        if n == len(needle):
            return h-n
        else:
            return -1

    def getnext(self,T:str)->List[int]:
        j=0
        k=-1
        next = [0 for i in range(len(T))]
        next[j]=k
        while j <len(T)-1:
            if k==-1 or T[j]==T[k]:
                j+=1
                k+=1
                next[j] = k
            else:
                k = next[k]
        return next