你好呀!
这里记录我的学习经历和内容
希望能够帮到你们
: )
标签对应使用的编程语言
分类中查看对应的板块
标签对应使用的编程语言
分类中查看对应的板块
我们已经学会了基本的数字电路逻辑和状态机的思想,现在我们要着手实现一个简单的处理器。首先我们需要明确接下来要实现的指令集sLSA和处理器的细节:
01 | 7 6 5 4 3 2 1 0 |
接下来完成实验的任务:
通过多路选择器实现一个ROM, 并在其中存放数列求和的指令序列, 然后通过PC寄存器取出指令. 你需要根据你的理解来确定ROM的规格.
先把数列求和的指令翻译成机器码,以1+2+3+...+10为例:
1 | 0: li r0, 10 |
然后将数据硬编码到我们的ROM中,并通过PC进行取值:
图中左上是PC寄存器,负责提供地址。右边这一堆是编码的ROM存储电路,可以将我们的数列求和程序读取出来
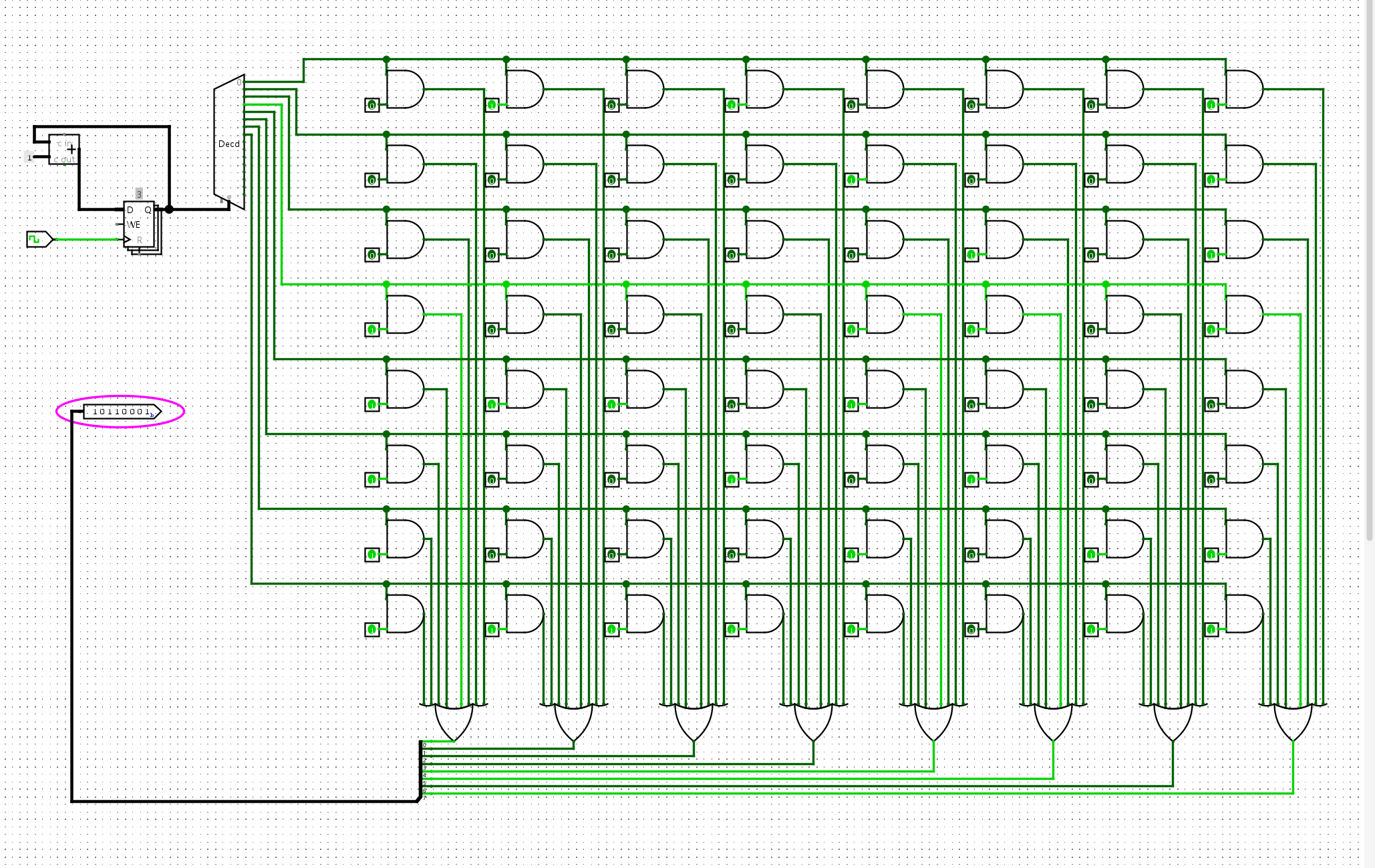
在寄存器的基础上搭建一个RAM, 从而实现GPR的写入功能. 你需要根据你的理解来确定RAM的规格.
我们的GPR有4个寄存器,每个寄存器存储八位的数据。可以简单设计如下:
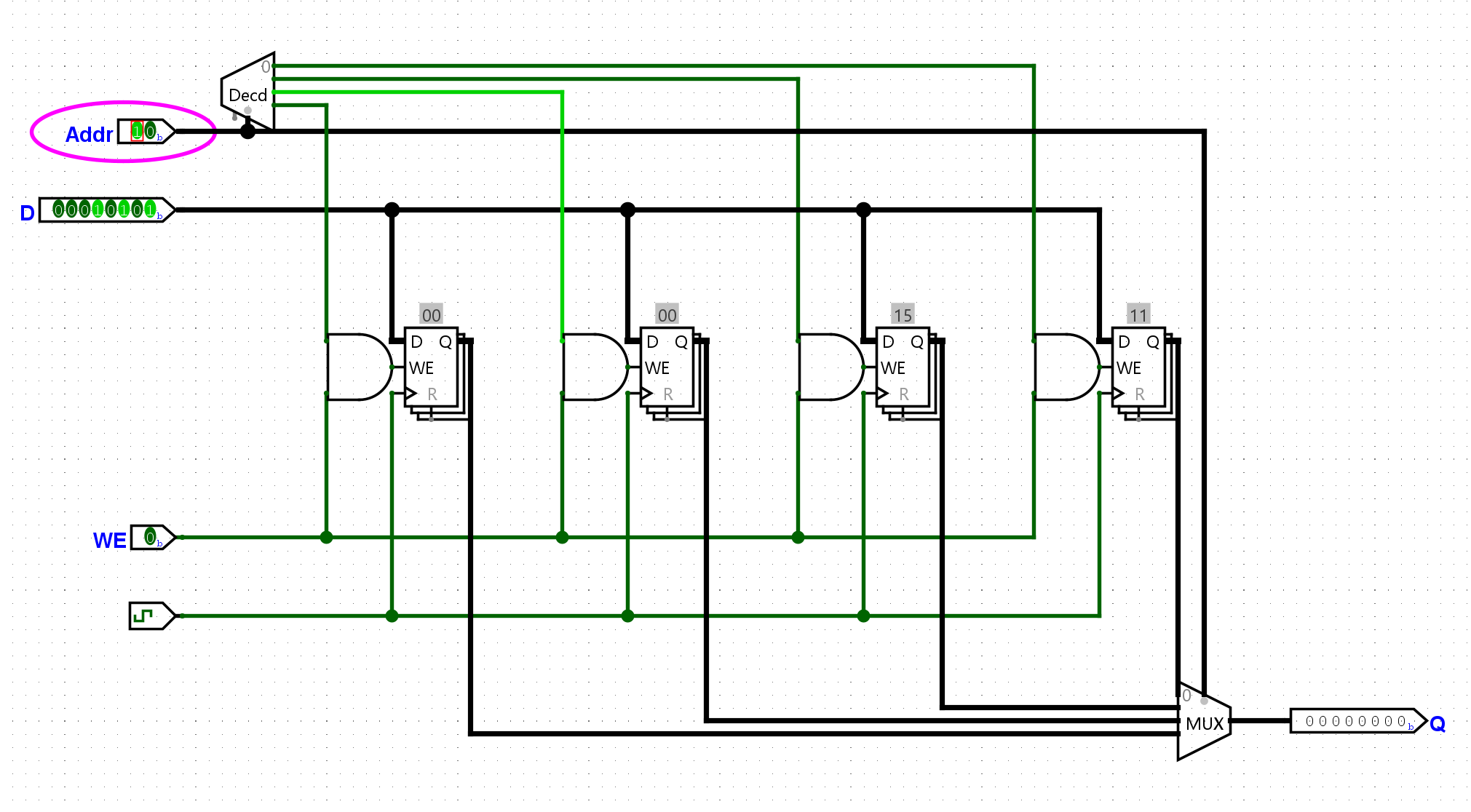
根据上文, 用数字电路实现
li的指令周期涉及的各个部件, 并将它们连接起来. 实现后, 尝试让sCPU执行数列求和程序中的前几条li指令, 并观察电路中GPR的状态是否与ISA的状态一致.
成功的从ROM中向寄存器写入了值:
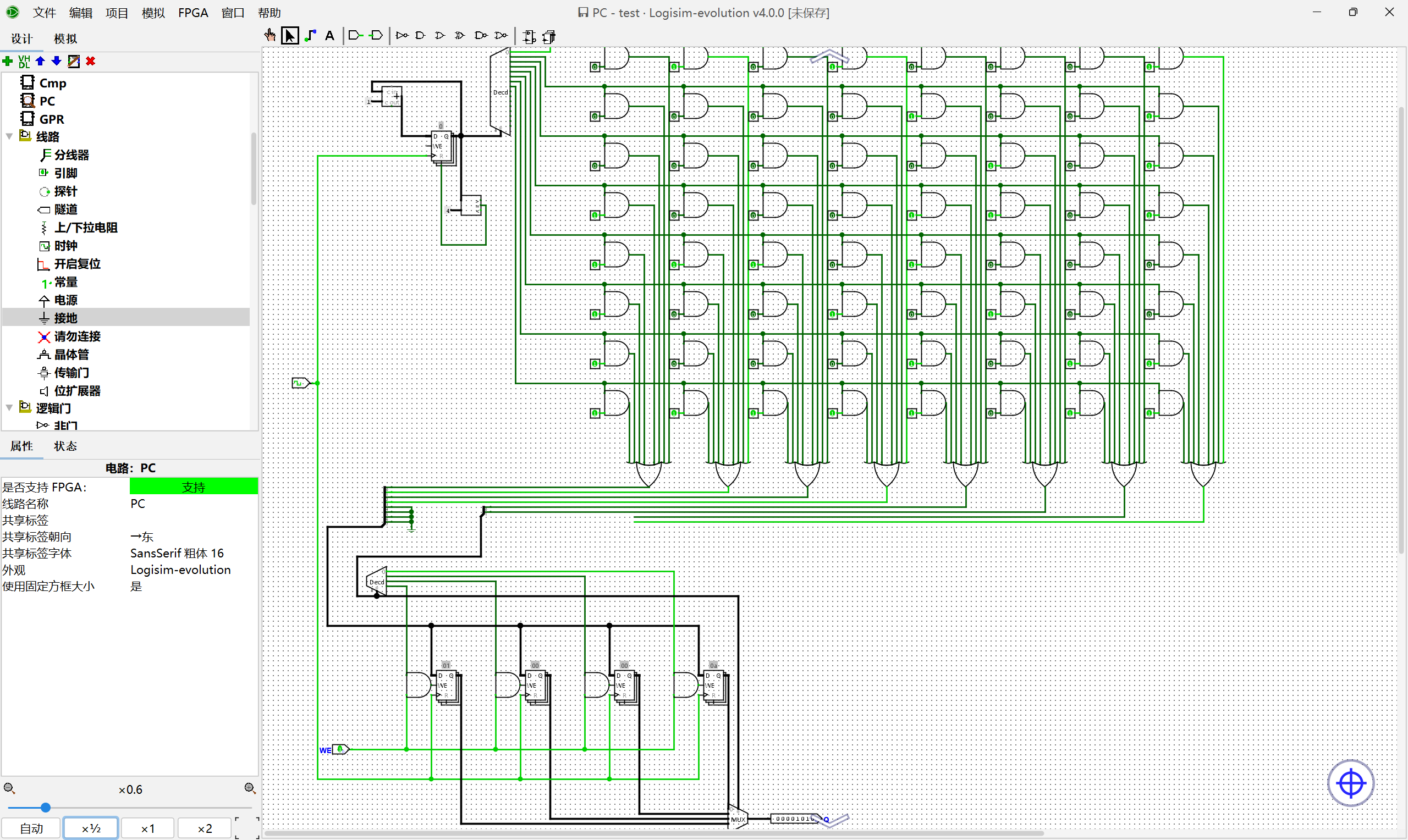
根据上文, 在sCPU中添加
add指令. 实现后, 尝试让sCPU继续执行数列求和程序中的几条add指令, 并观察电路中GPR的状态是否与ISA的状态一致.
经过上一个实验,现在我们的寄存器已经能够成功的接受写入了。但是为了实现进一步的指令支持,我们需要将我们的GPR优化并封装起来,我们需要实现以下端口:
raddr1(读地址),
rdata1(读数据)raddr2, rdata2waddr(写地址), wdata(写数据),
wen(写使能), clk(时钟)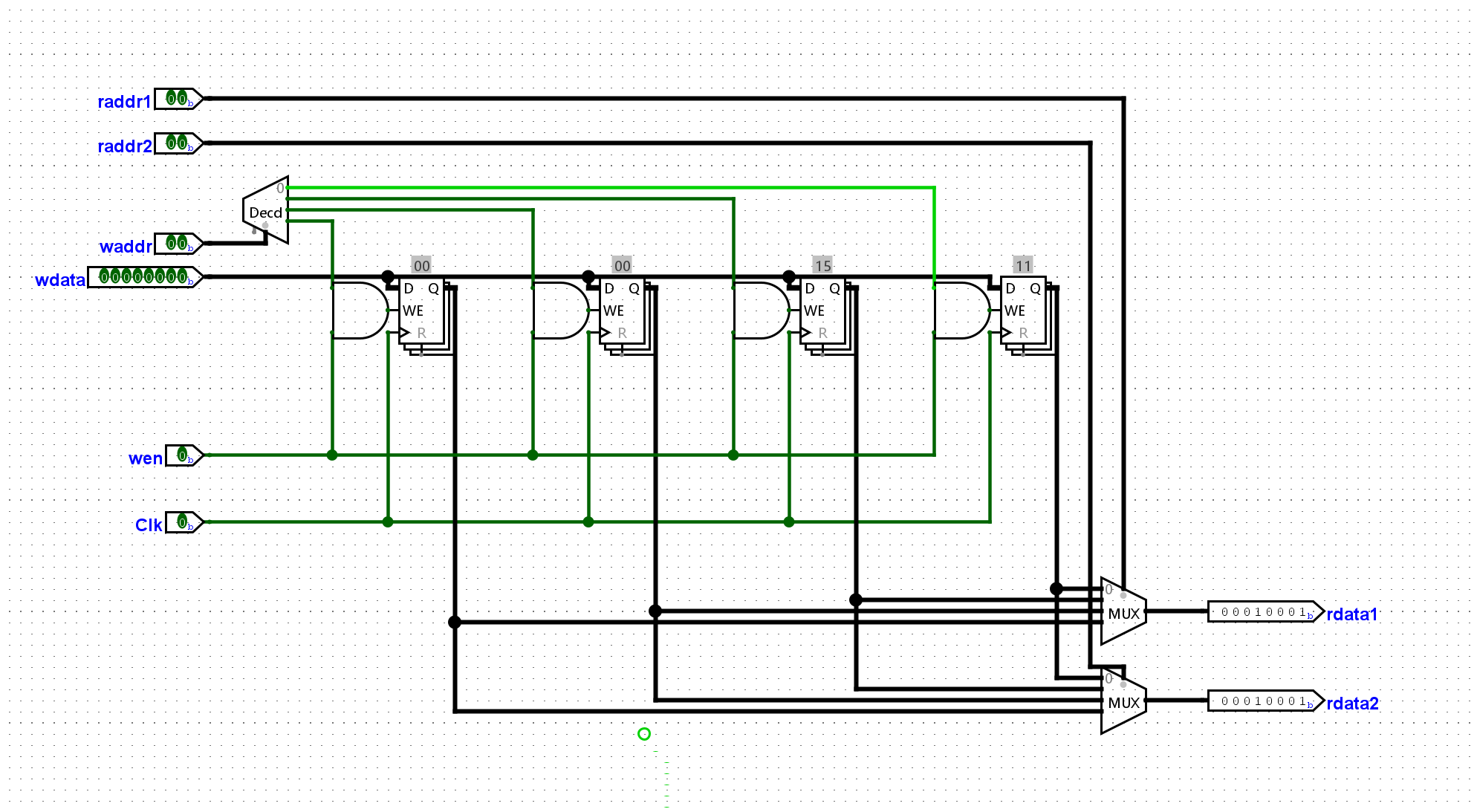
这样我们就能满足add指令,同时读取两个源操作数和写入一个寄存器的操作了。
但是再次之前我们还需要进一步实现译码功能,从而将我们的add和li逻辑分离,不同的指令需要不同的信号:
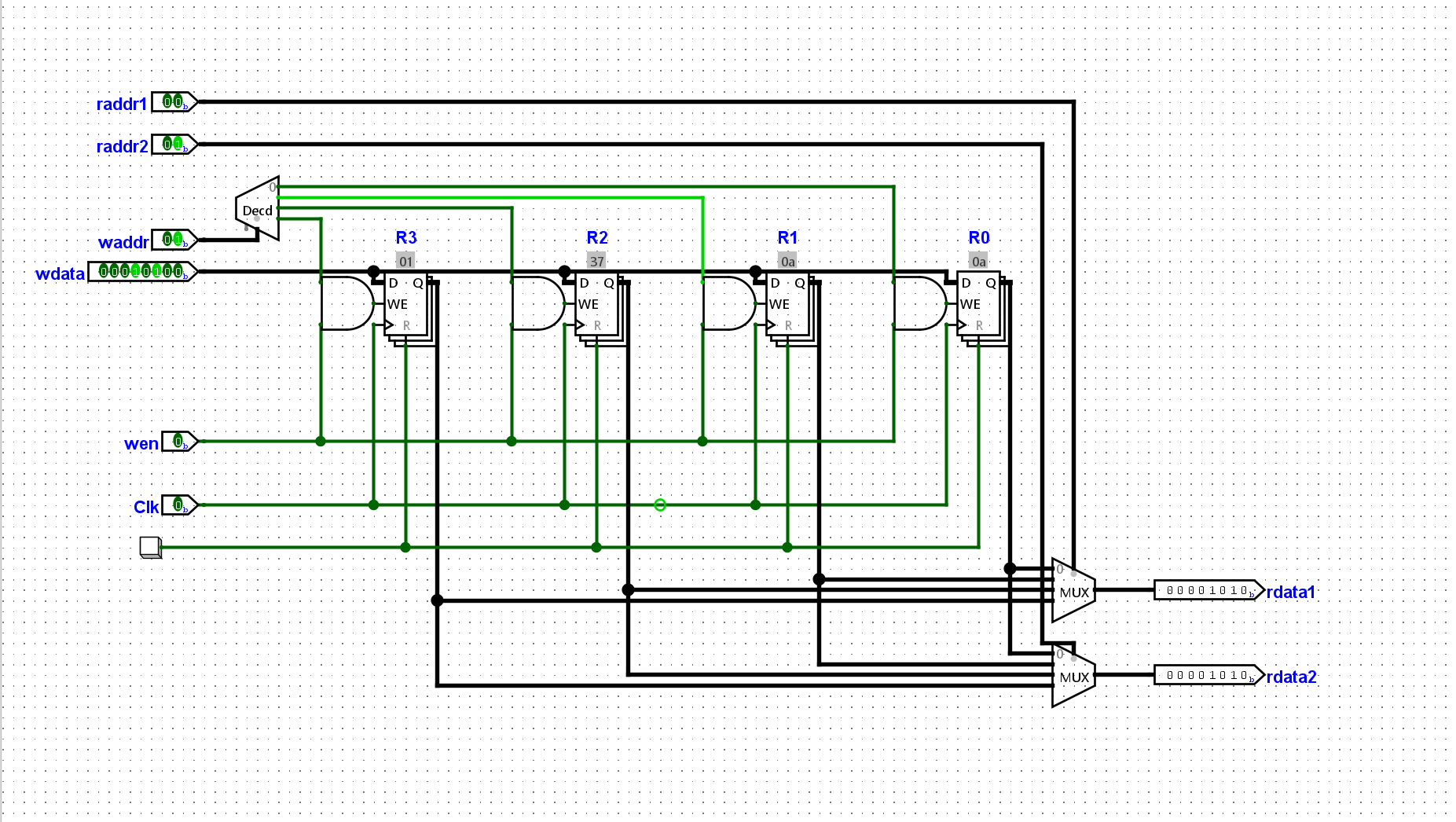
waddr和imm作为输入,需要写使能信号开启raddr1和raddr2作为输入rdata1和rdata2,做加法输入到wdatawdata、waddr和写使能信号,更新寄存器综上,我们可以规划出我们的电路图,以完成前6条指令的执行:
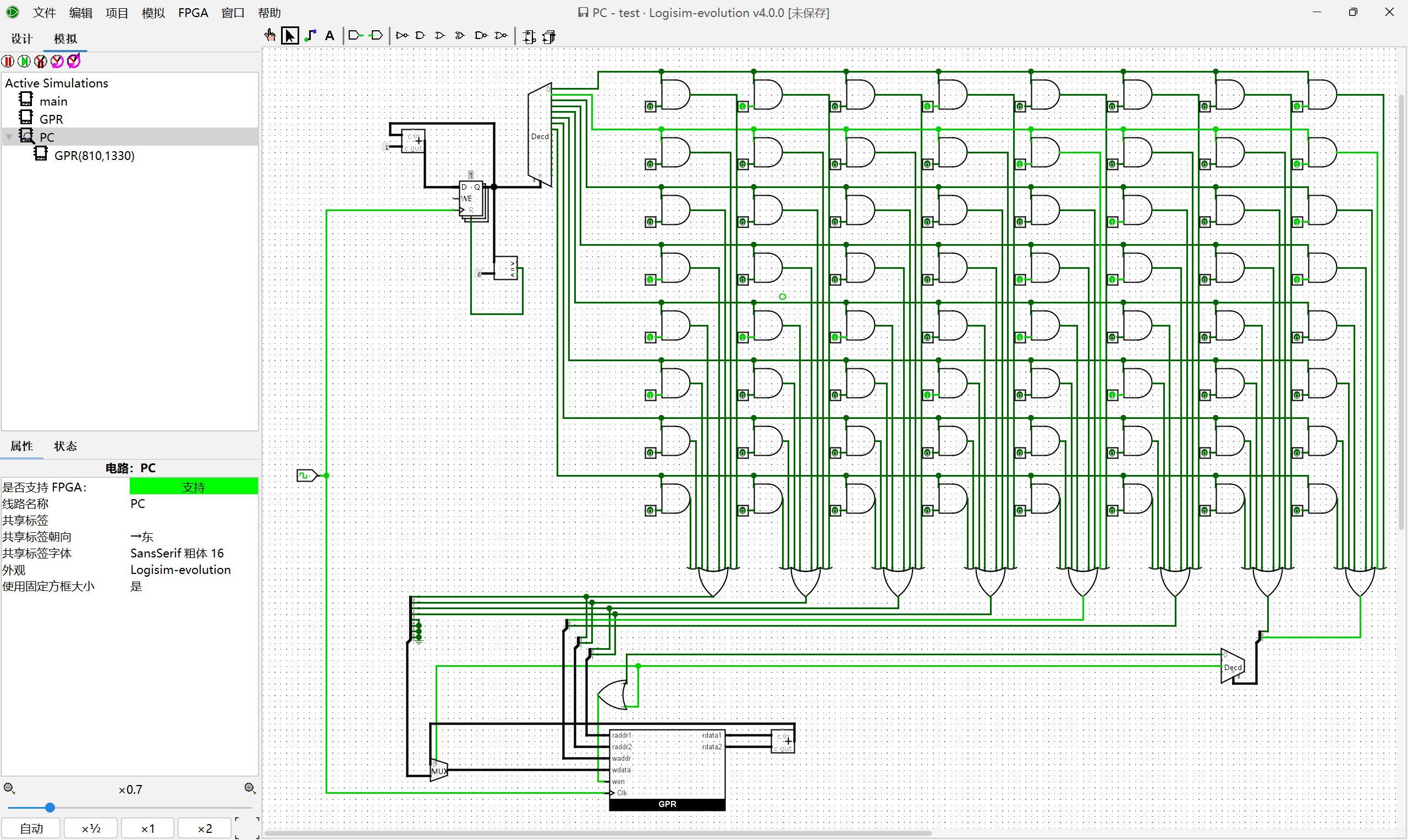
以下是执行一轮前六条指令后的寄存器状态:
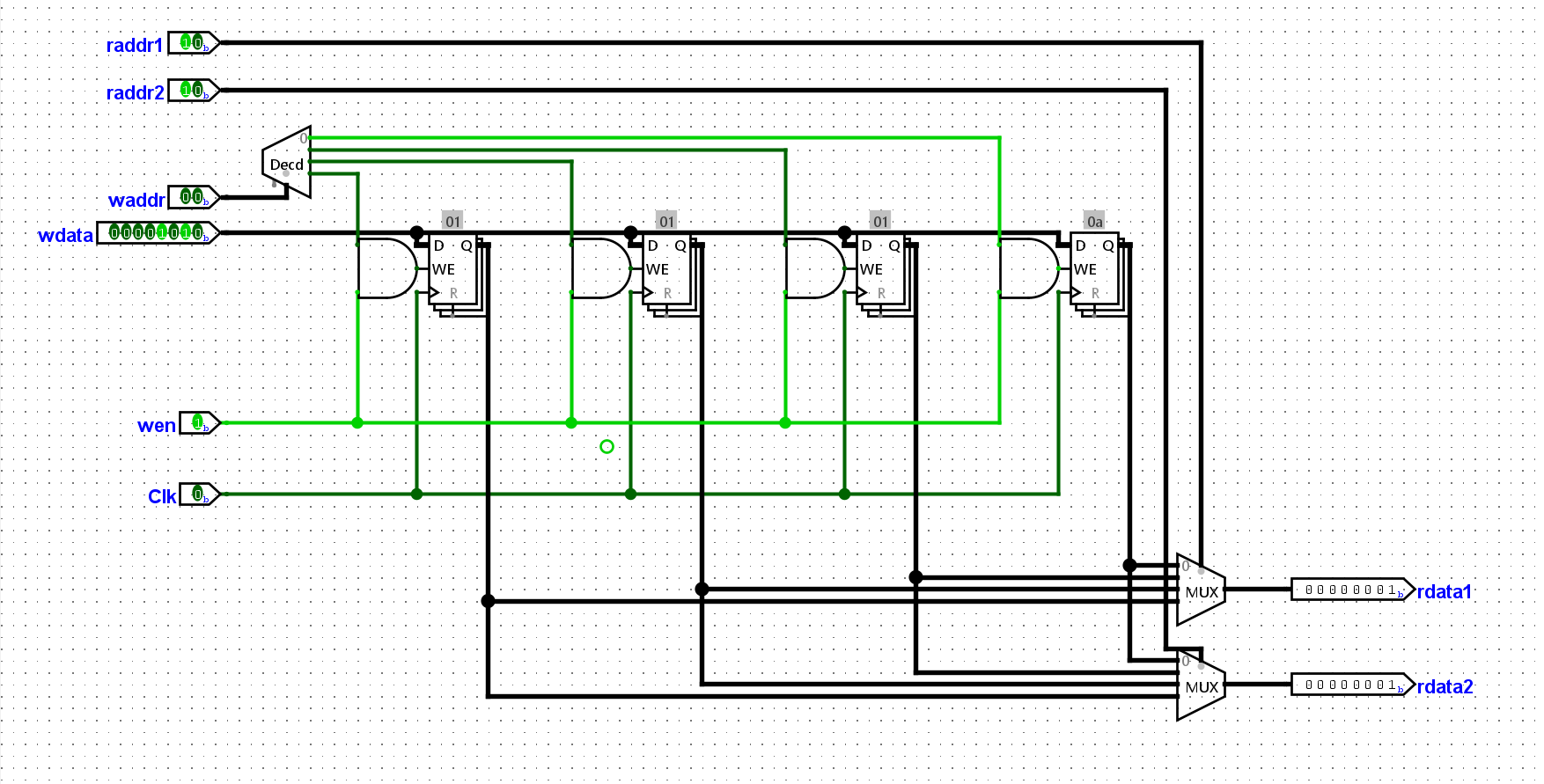
根据上文, 在sCPU中添加
bner0指令. 实现后, 尝试让sCPU执行完整的数列求和程序, 如果你的实现正确, 你应该能看到PC最终为7, 且在某GPR中存放求和结果55.
添加bner0我们首先分析他需要哪些输入和信号:
addr用于改变PC的值,也就是说我们现在需要一个机制能支持我们改变PC的内容r0和r2的值进行比对,如果不同则跳转这两个问题都可以简单的通过多路复用器的思路来解决:
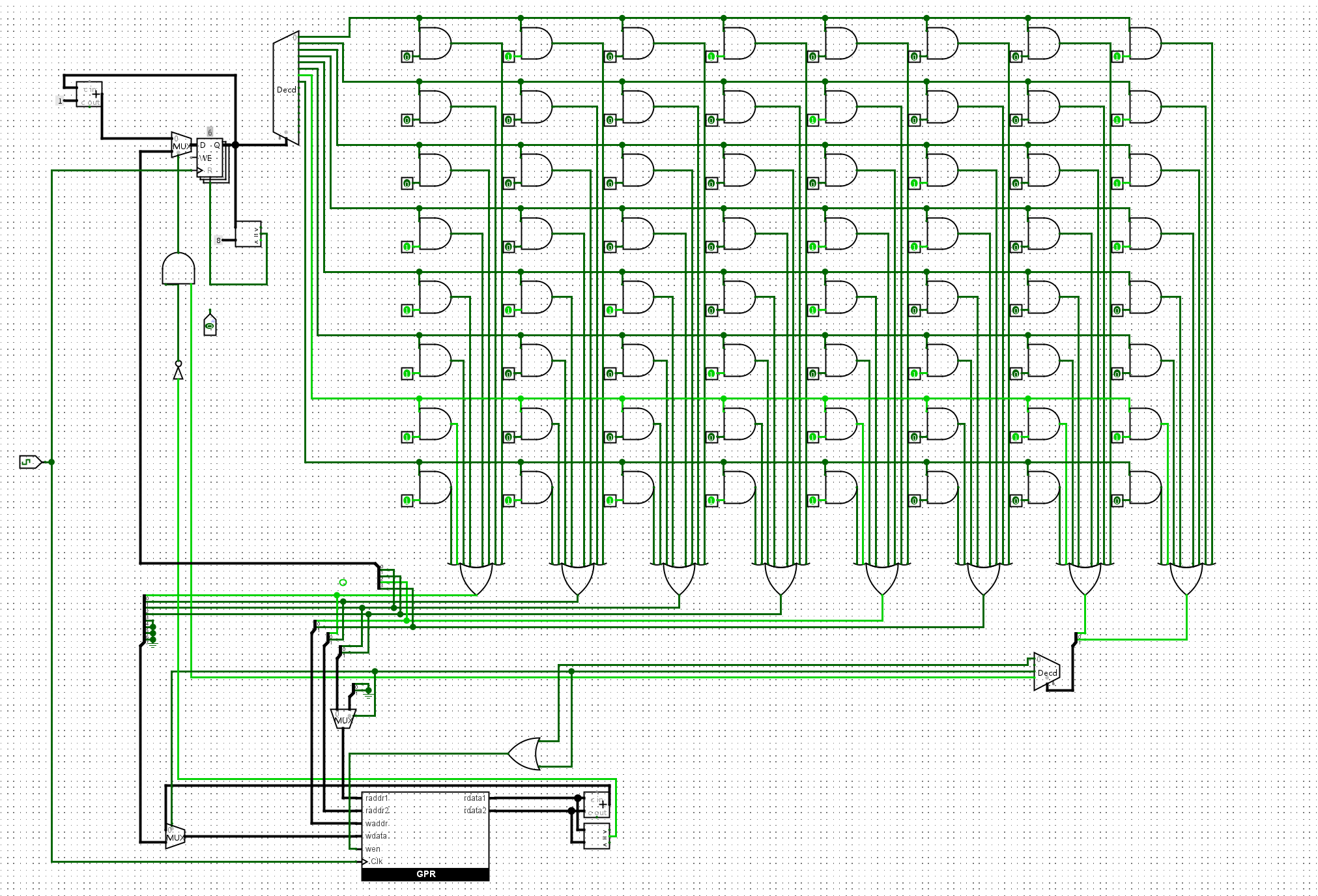
我们的求和程序运行的最终情况如下。可以看到r2 = 0x37 = 55符合我们的预期:
在学习数字电路时, 有一道必做题要求你通过寄存器和加法器, 计算出
1+2+...+10的结果. 现在你用sCPU完成了同样的计算, 尝试对比两个方案各有什么优点和缺点.
先前的数字求和电路,是通过设计电路的模式来实现”程序”的运行,那种行为类似于程序中的硬编码,比较死板,而且不方便改动。我们每想运行一个程序都需要重新设计一个电路。
但是想这种通过操控寄存器的方法,明显为我们带来了更好的可拓展性,我们可以通过现有的三个指令,运行各种加法程序。我们只需要对指令的内容进行改动就好了,这给我们带来了更好的可拓展性。所以我认为这是一种进步。不过相应的,为了满足电路能够运行指令,我们的设计也会更加的复杂,无法像先前的电路一样轻便。
编写一段指令序列, 计算10以内的奇数之和, 即
1+3+5+7+9. 然后尝试用你设计的sCPU指令这段指令序列, 检查运行结果是否符合预期
首先我们需要为其编写相应的指令:
1 | 0: li r0, 11 |
然后将程序编写进我们的ROM中,执行得到结果如下(R2 = 0x19 = 25):
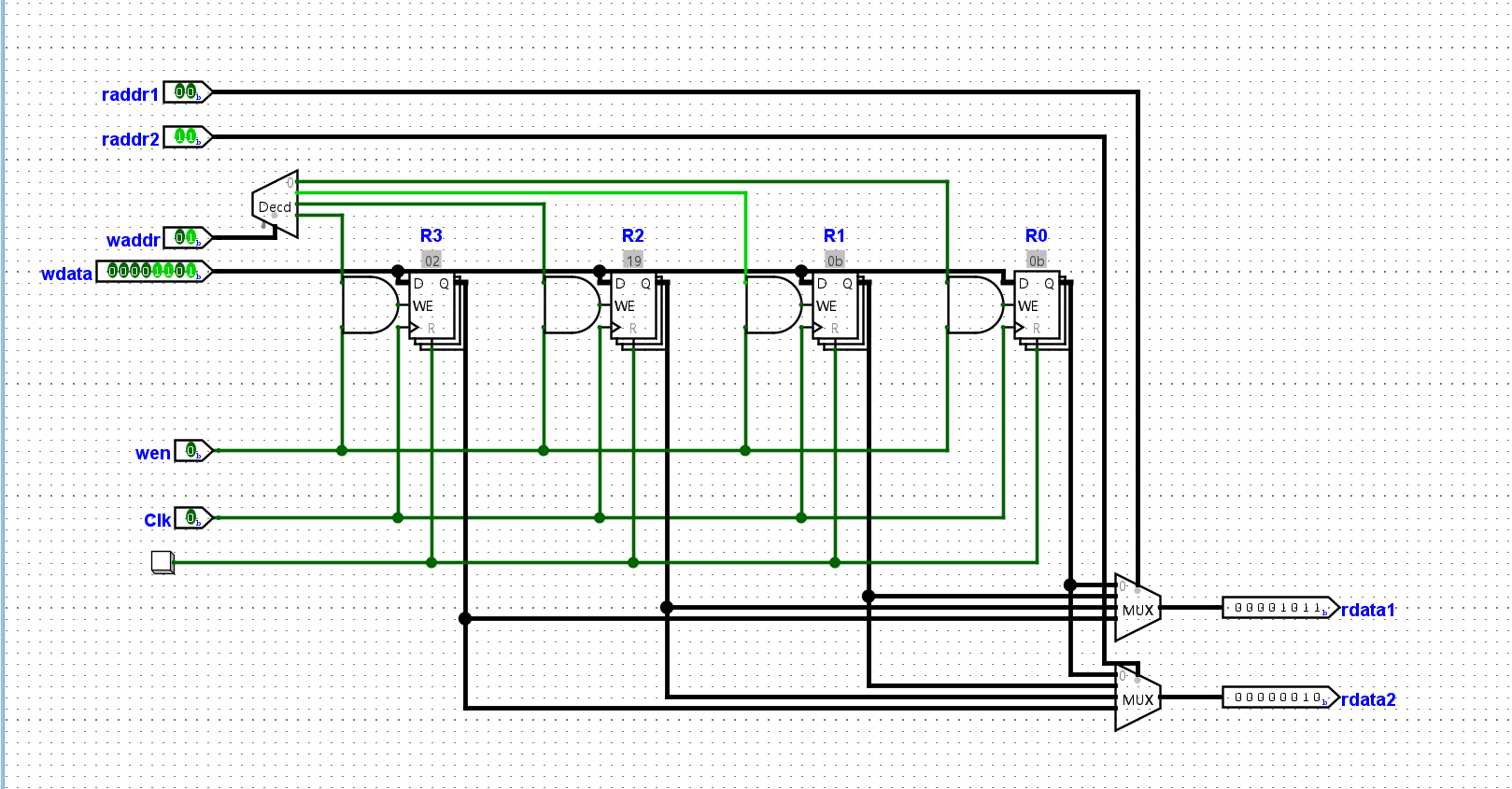
尝试为sISA添加一条新指令
out rs, 执行该指令后, 会将R[rs]以十六进制的形式输出到七段数码管. 你可以自行决定这条指令的编码.然后, 在sCPU中实现
out指令, 并修改数列求和程序, 使得在计算出结果后, 能在七段数码管中显示计算结果.
首先向我们的ISA中添加out的格式:
1 | 7 6 5 4 3 2 1 0 |
这个指令只需要读取rs2作为输入就可以了,所以我们添加一个显示内容的电路,就可以完成啦:
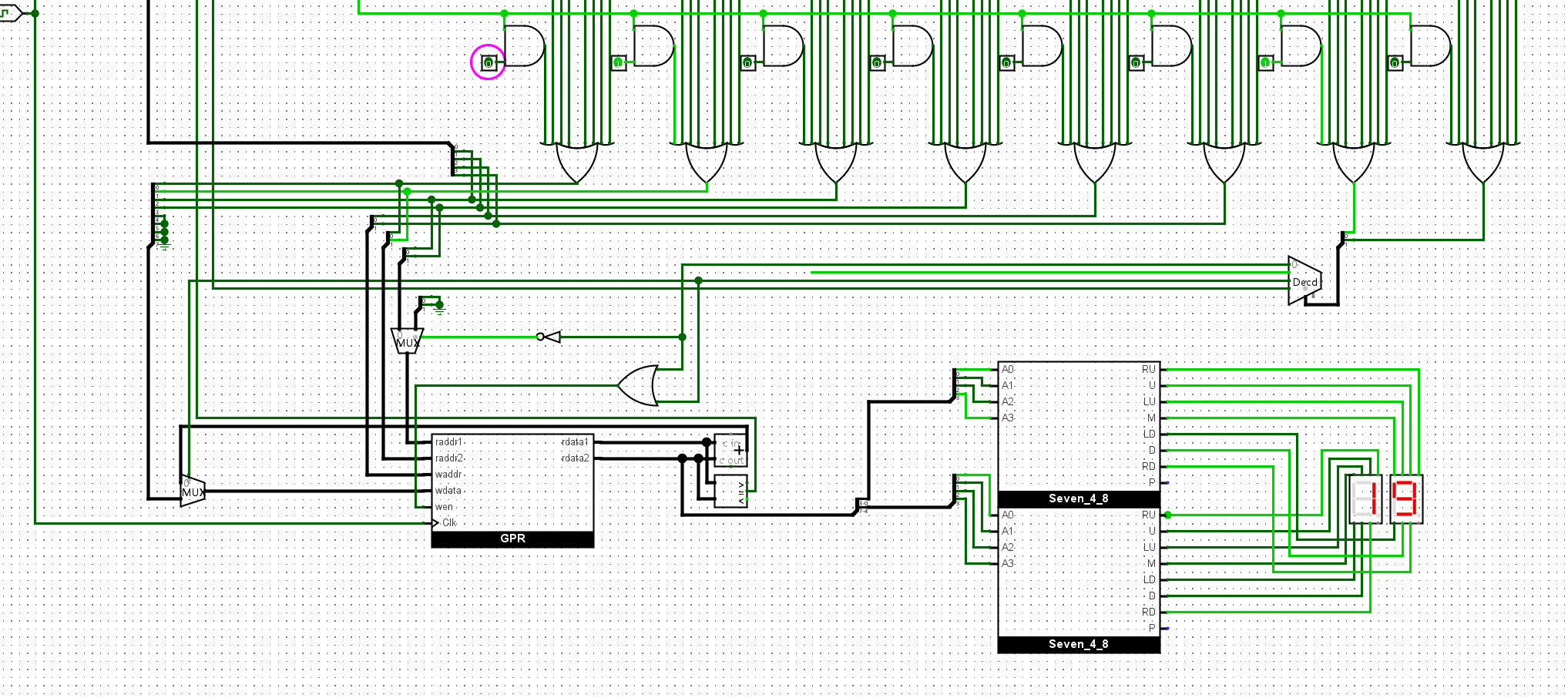
尝试继续执行指令, 记录寄存器的状态变化过程. 你发现执行到最后时, 处理器处于什么样的状态? 上述数列的求和结果在哪个寄存器中?
1 | 0: li r0, 10 # 这里是十进制的10 |
状态机视角的寄存器状态变化:
1 | PC r0 r1 r2 r3 |
尝试用上述指令编写一个程序, 求出10以内的奇数之和, 即计算
1+3+5+7+9. 编写后, 尝试列出处理器状态的变化过程, 以此来检查你编写的程序是否正确.
编写程序如下:
1 | 0: li r0, 11 |
处理器状态如下:
1 | PC r0 r1 r2 r3 |
见课件
你可以在Compiler Explorer这个在线网站中运行上述C程序. 具体地, 在代码编辑器中输入上述C代码后, 点击编辑器上方工具栏的
Add new..., 选择Execution Only, 即可弹出执行结果的终端窗口. 如果你的操作正确, 你将看到终端窗口输出z = 3.你可以尝试按照你的理解修改C代码, 并观察程序的输出.
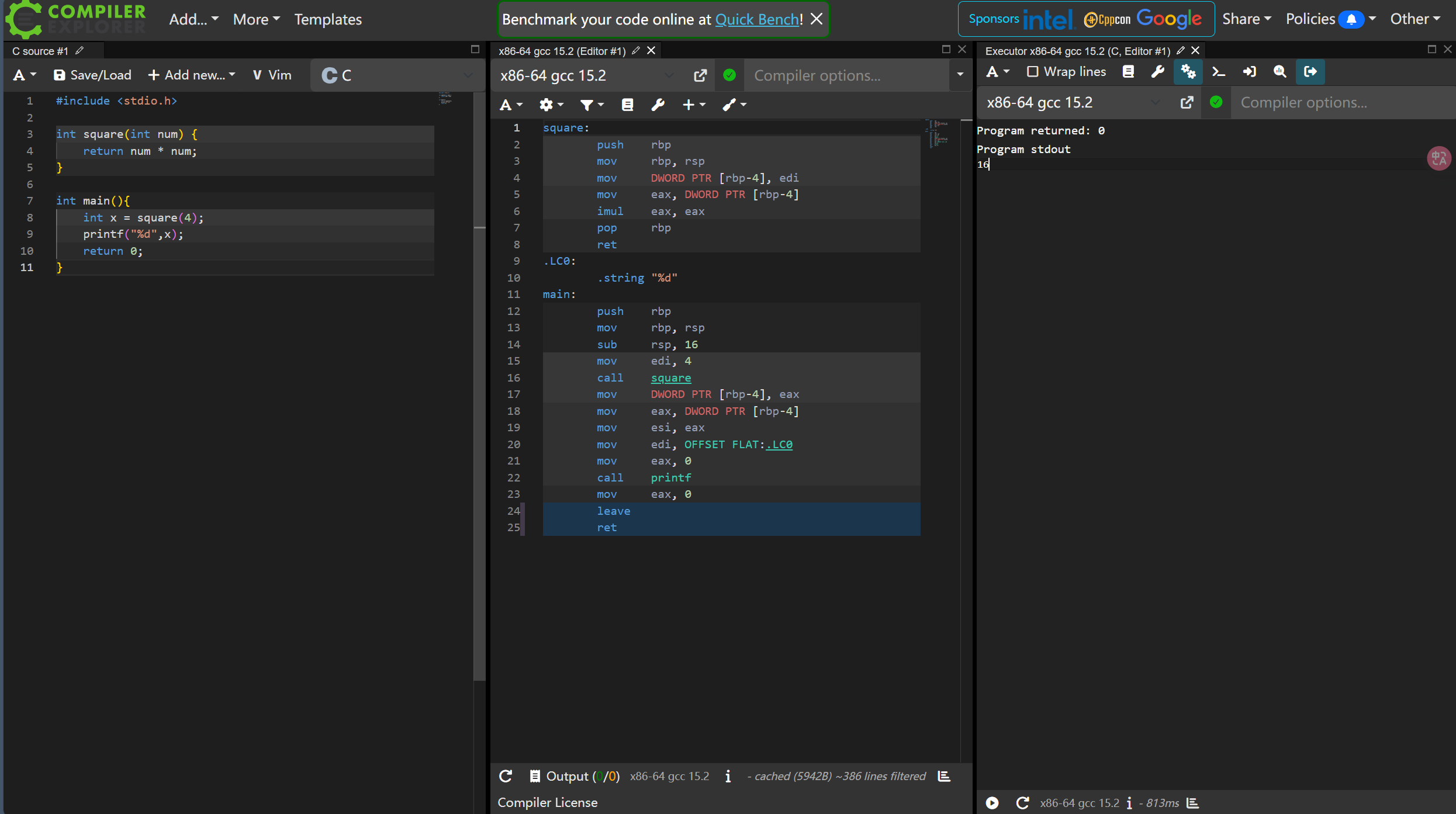
尝试继续执行上述代码, 记录状态的变化过程. 程序执行结束时, 程序处于什么样的状态?
1 | // 待执行的程序 |
状态:
1 | PC sum i |
在上一小节中, 你已经通过寄存器和加法器搭建出一个简单数列求和电路, 用于计算
1+2+...+10. 尝试列出电路状态的变化过程.
这个是上一节中搭建的用于数列求和的电路
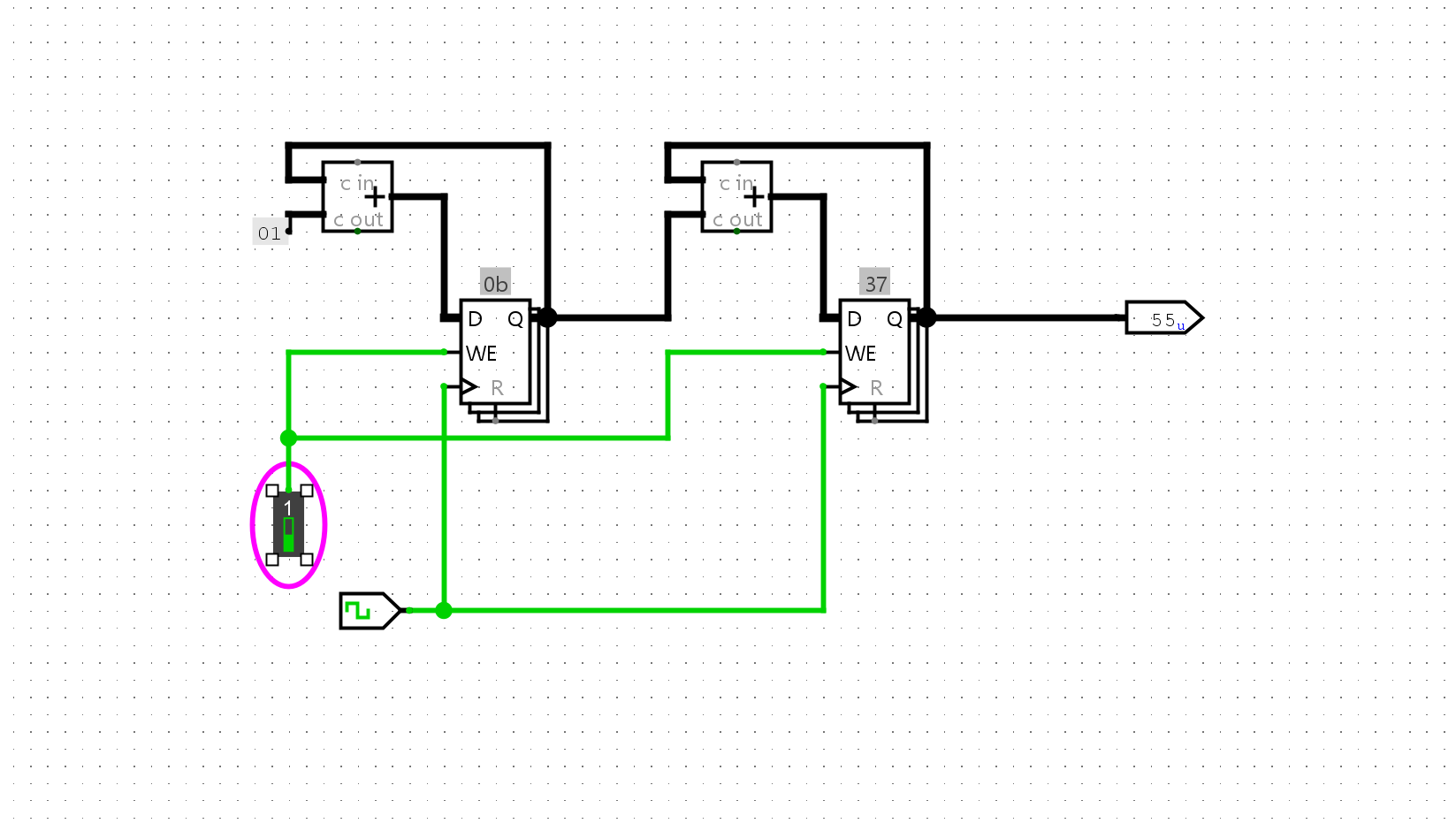
我们将左边的寄存器视作状态A 右边的寄存器视作状态B,那么有状态:
1 | A B |
我们已经给出了数列求和的C程序和相应的指令序列, 尝试从状态机的视角理解它们之间的联系.
对比先前的C程序和指令序列的状态迁移过程,我们可以发现他们的在逻辑上等价的:
结合老师上课讲的内容,他们可以被视作是等价的。
具体地, 点击编辑器上方工具栏的
Add new..., 选择Compiler, 即可弹出相应汇编代码的窗口. 汇编代码默认采用x86指令集, 你不一定能理解每一条指令的具体含义, 但通过背景颜色的高亮和鼠标移动, 你可以看到C程序片段和汇编代码片段之间的对应关系.
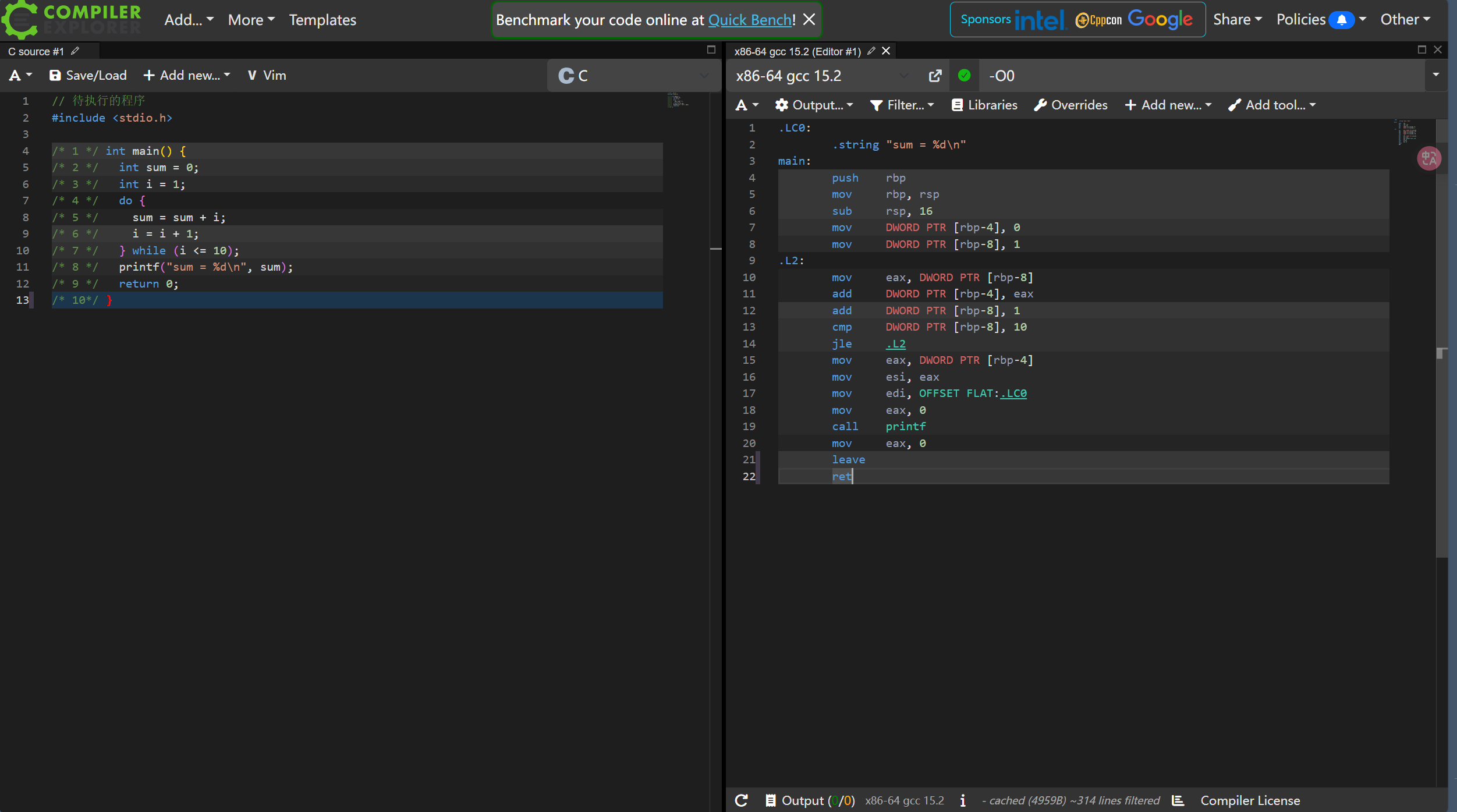
接着学习F3的内容
主要讲了原码、补码、反码,这些是计算机组成的基本知识,就不做过多赘述。
根据4位加法器的设计思路, 尝试在Logisim中通过门电路搭建一个4位减法器, 用七段数码管按十六进制显示减法器的两个输入和结果, 并用一个LED灯指示减法结果是否产生借位. 搭建后, 通过仿真检查你的方案是否正确.
这里的话我们先从一位减法器开始实现,实现的原理实际上和全加器是一样的。只不过这里需要注意借位的条件,全加器和减法器的区别就在于进位和借位信号的实现,以下是一个简单的一位减法器实现:
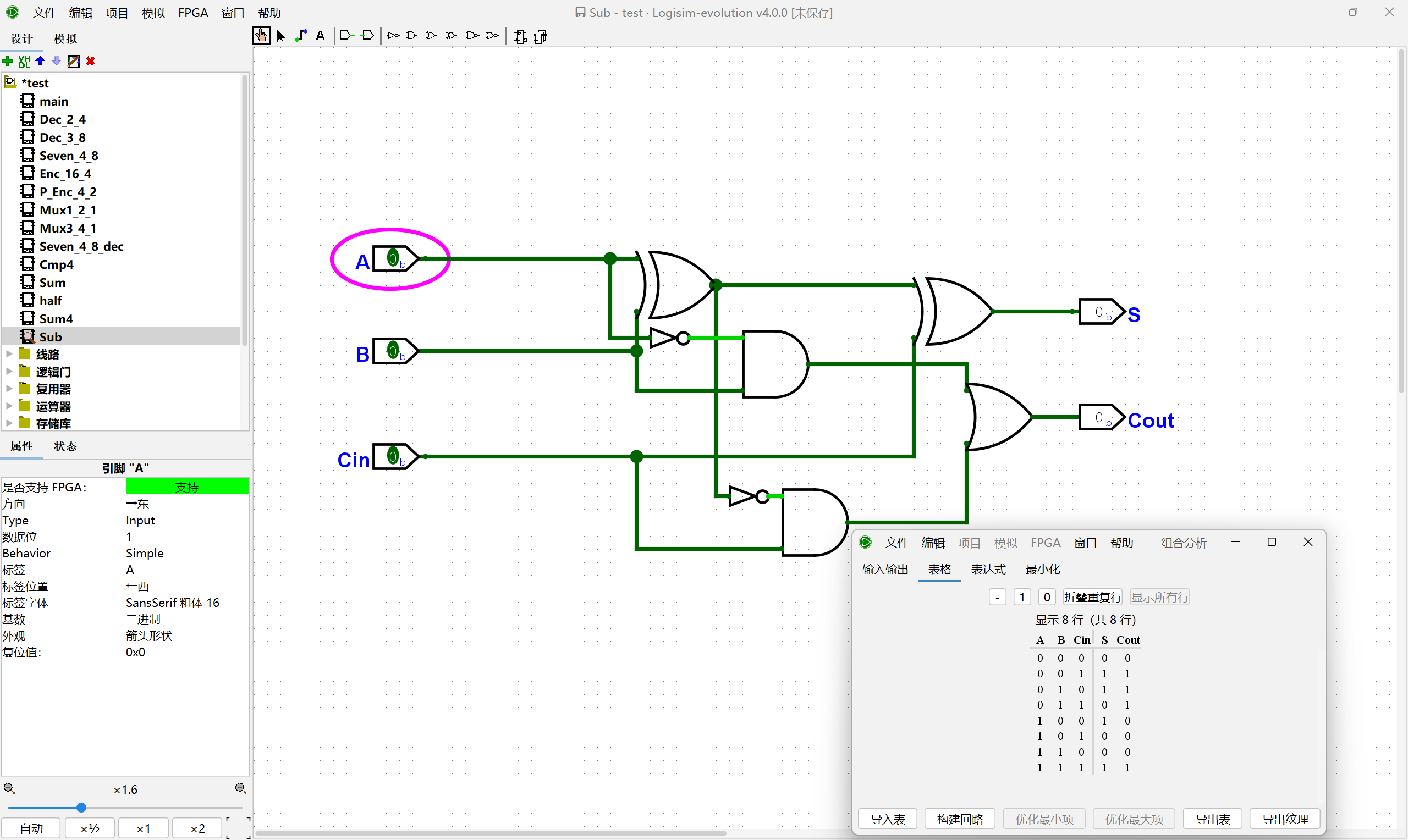
在此基础之上,我们实现四位的减法器:(实现同加法器)
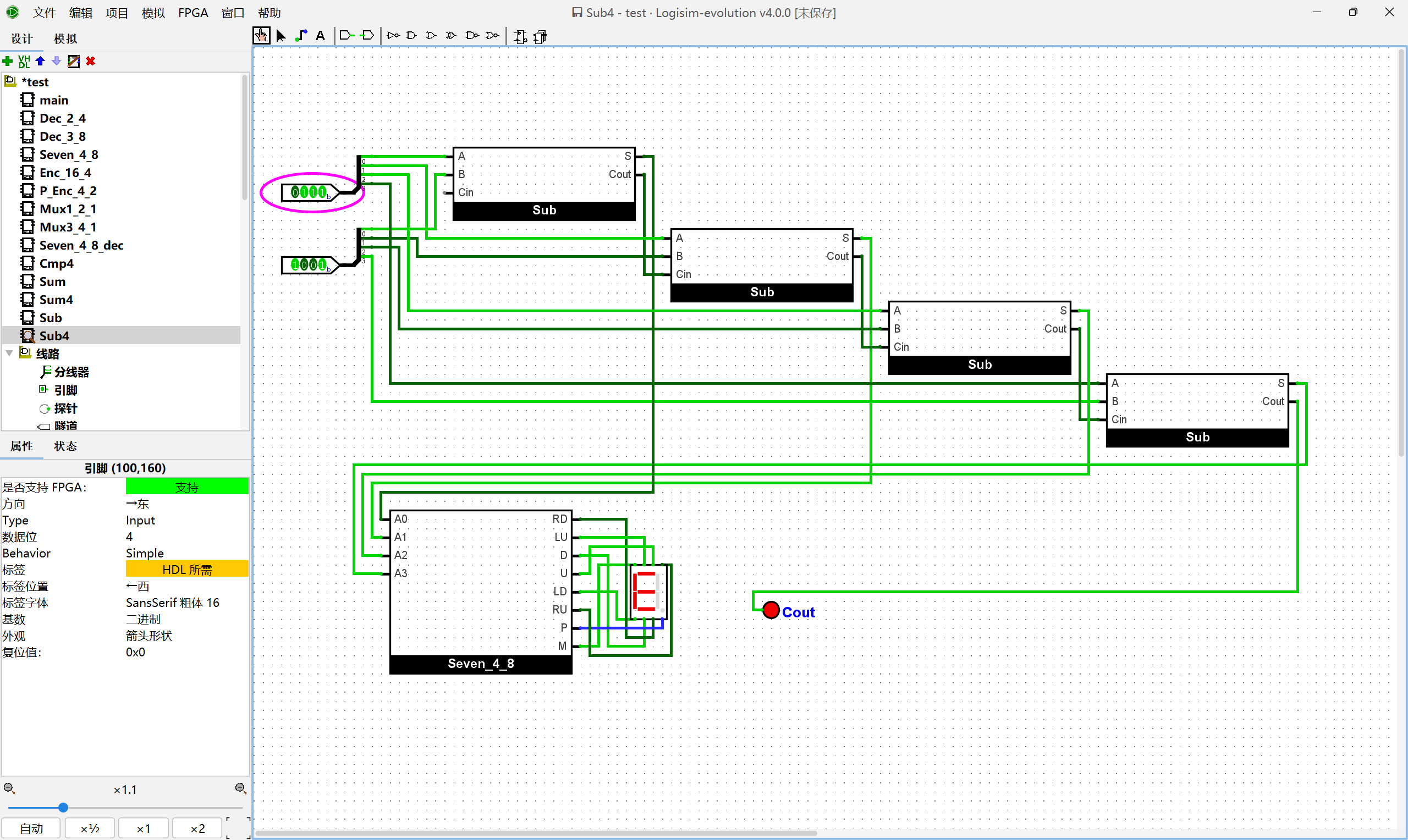
理解原码加法器的工作原理后, 尝试用加法器, 减法器和多路选择器等部件, 在Logisim中搭建一个4位原码加法器. 为了显示符号位, 你可以额外实例化一个七段数码管, 结果为负数时显示负号
-, 否则不显示. 搭建后, 通过仿真检查你的方案是否正确.
实现原码加法器需要进行分类讨论的情况:
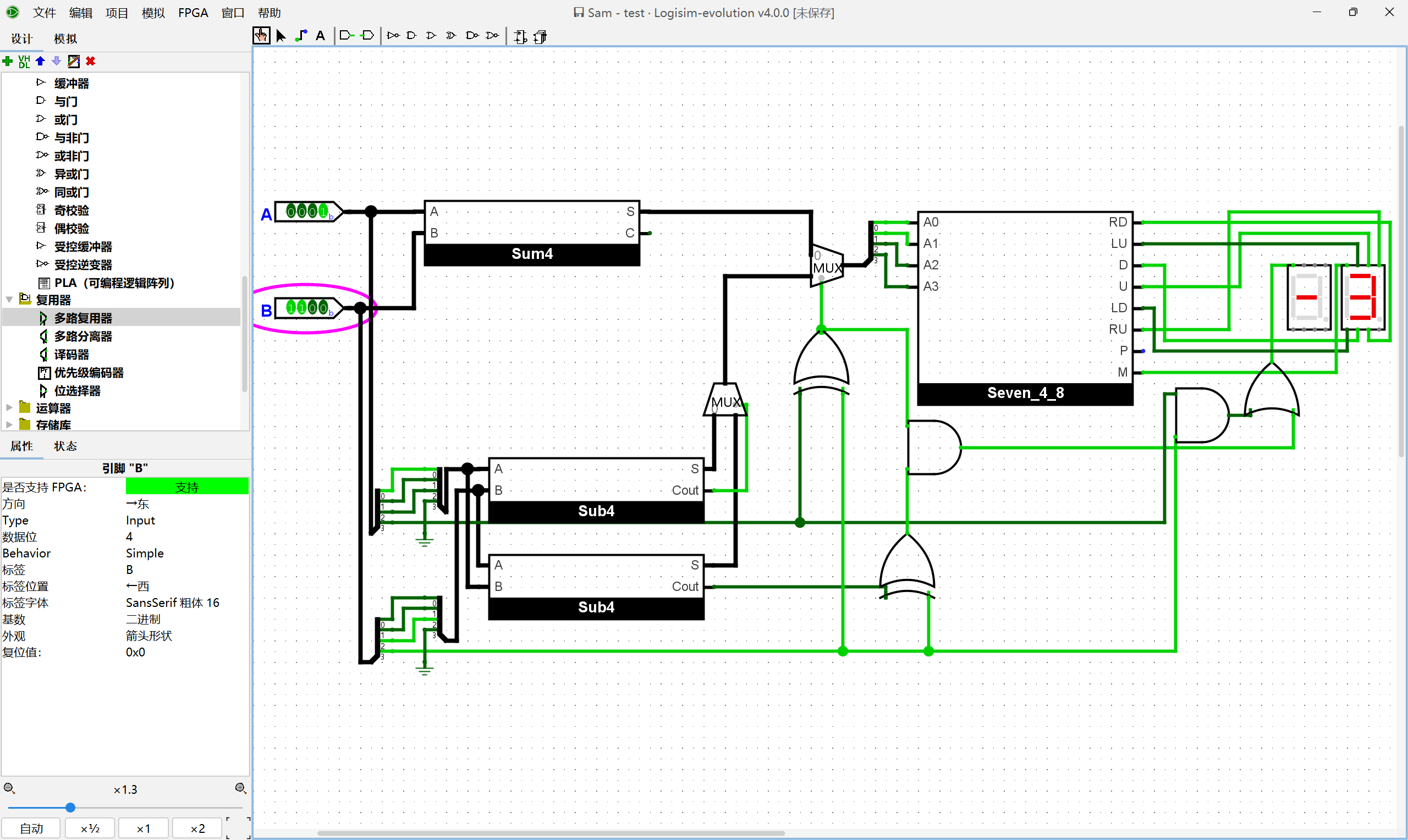
尝试按照上述思路, 在Logisim中搭建一个4位反码加法器. 搭建后, 通过仿真检查你的方案是否正确.
我们只需要对输入进行预处理,将反码转换为原码作为输入就可以了。转换电路的实现也很简单,如果反码是正数则保持不变,如果是负数,则翻转数值位,保持符号位。
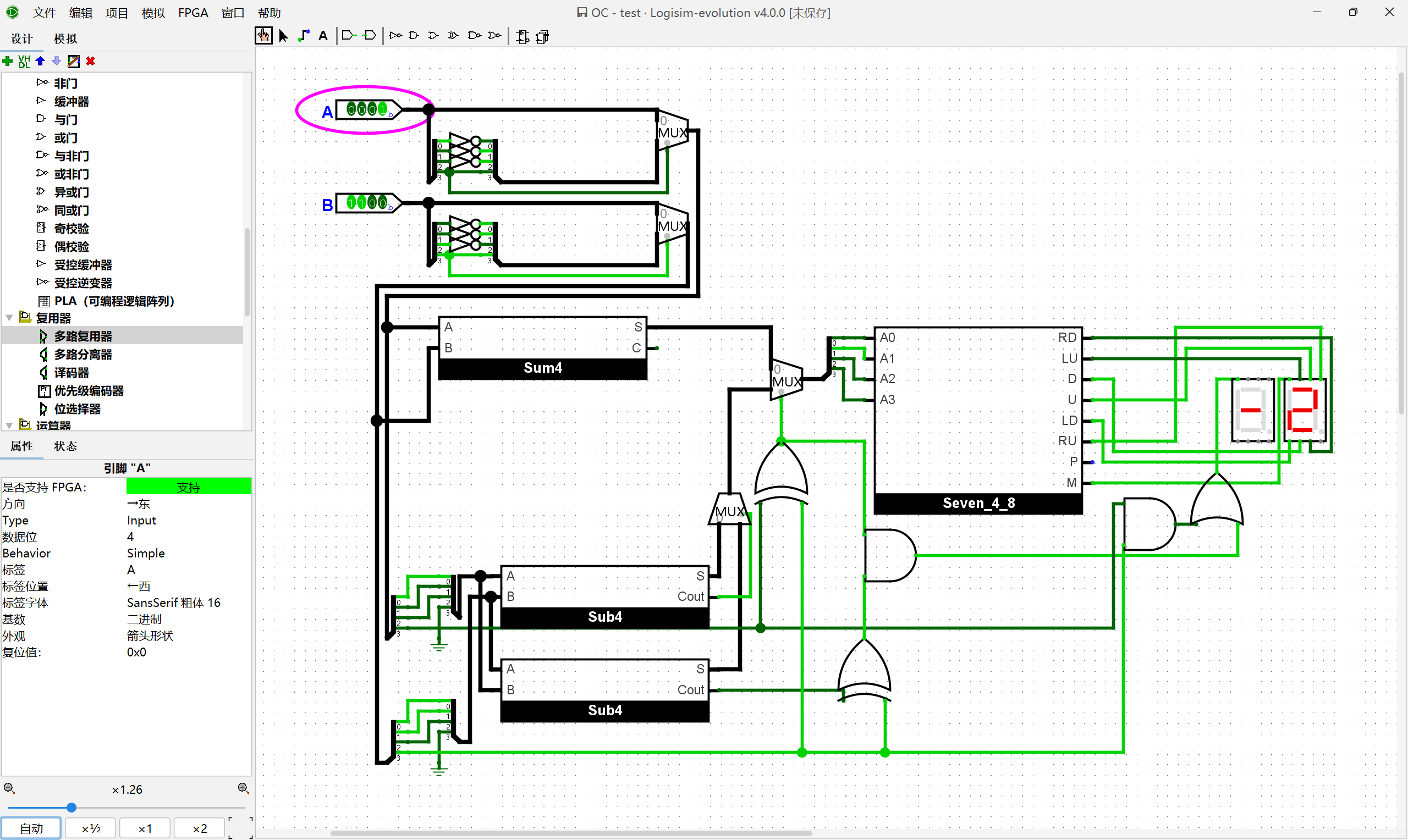
将上述真值表补充完整, 尝试列出溢出条件的逻辑表达式. 然后在Logisim中在4位加法器的基础上添加溢出判断逻辑. 添加后, 通过仿真检查你的方案是否正确.
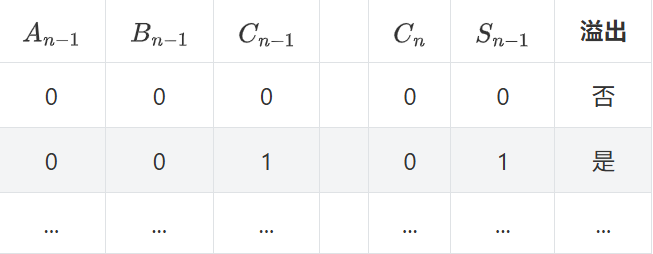
首先完成表格:
| As | Bs | Cin | Cout | Ss | 溢出 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 否 | |
| 0 | 0 | 1 | 0 | 1 | 是 | |
| 0 | 1 | 0 | 0 | 1 | 否 | |
| 0 | 1 | 1 | 1 | 0 | 否 | |
| 1 | 0 | 0 | 0 | 1 | 否 | |
| 1 | 0 | 1 | 1 | 0 | 否 | |
| 1 | 1 | 0 | 1 | 0 | 是 | |
| 1 | 1 | 1 | 1 | 1 | 否 |
我们注意到只有Cin和Cout不同时,才会有溢出现象。所以我们可以通过简单的异或来判断溢出的现象:
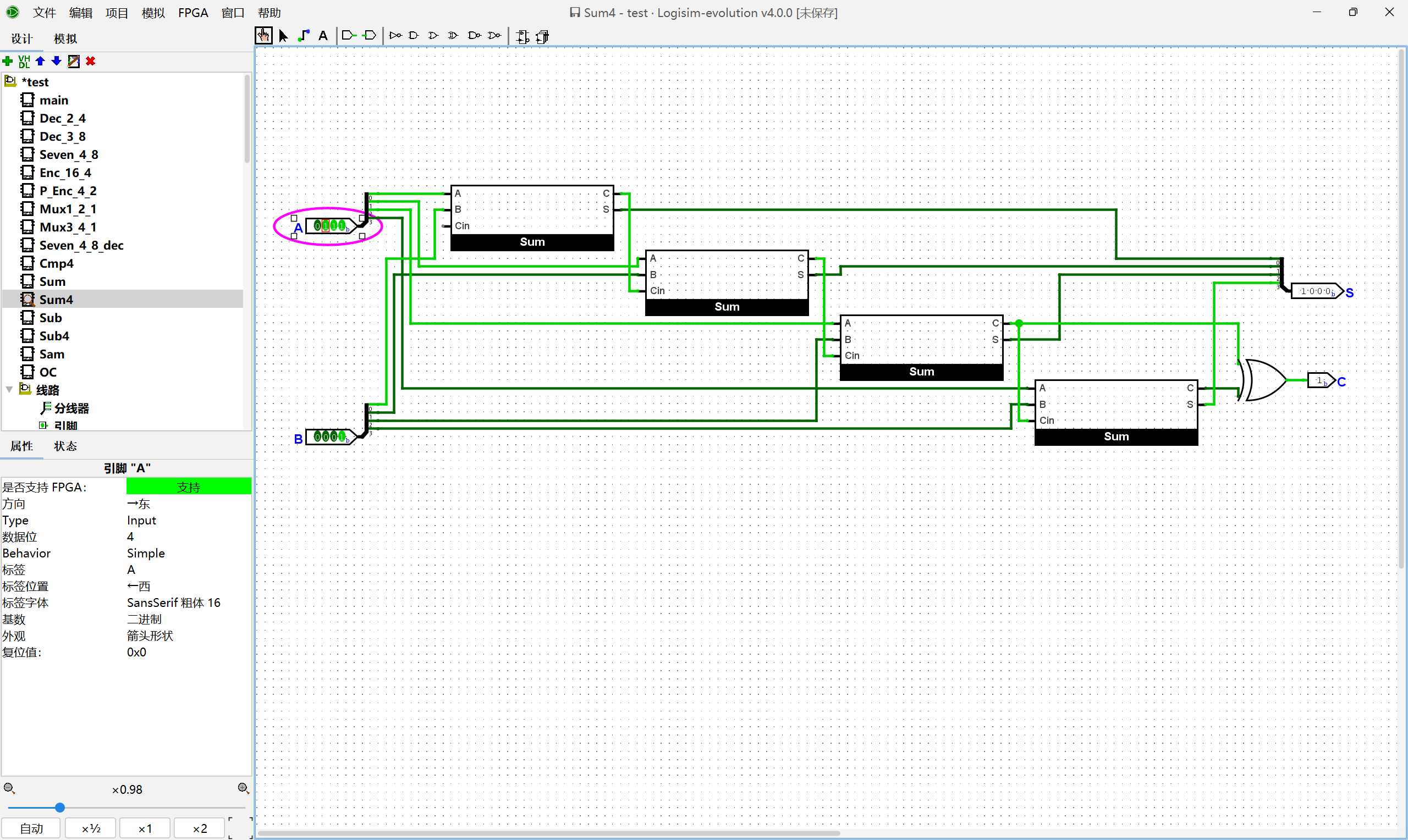
之前所设计的模块有一个特点,就是当前的电路状态完全由当前的输入状态决定。但只是这样子,我们并没办法实现大多数的功能。所以时序电路的设计就显得尤为重要。所以我们需要设计一种新的电路满足以下的两个要求:
具备上述特性的电路称为时序逻辑电路, 它可以存储状态, 其输出由当前输入和旧状态共同决定;而先前的电路我们成为组合逻辑电路。
尝试在Logisim中通过门电路搭建一个SR锁存器. 搭建后, 通过仿真检查你的方案是否正确.
由于手工操作时, 无法通过一次点击直接将两个拨码开关从
11变成00. 为了触发亚稳态, 你可以在SR锁存器前额外增加若干与门, 让另一个拨码开关同时控制这些与门的其中一个输入端, 这样就可以通过这一个拨码开关来让SR锁存器的两个输入端同时变成0了. 如果你成功触发了亚稳态, Logisim会在窗口底部显示Oscillation apparent的信息. 此时仿真将无法继续, 你需要通过Logisim的菜单重置仿真.
这里可以通过在模拟暂停的后设置输入的行为来触发亚稳态,可以看到电路中发生了振荡状态。
尝试根据电路结构图列出真值表, 分析D锁存器的行为.
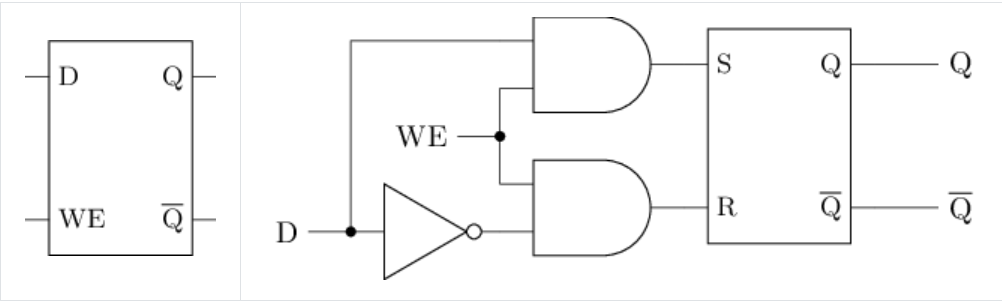
真值表如下:
| D | WE | Q | |
|---|---|---|---|
| 0 | 0 | X | |
| 0 | 1 | 0 | |
| 1 | 0 | X | |
| 1 | 1 | 1 |
尝试在Logisim中通过门电路搭建一个D锁存器. 搭建后, 通过仿真检查你的方案是否正确.
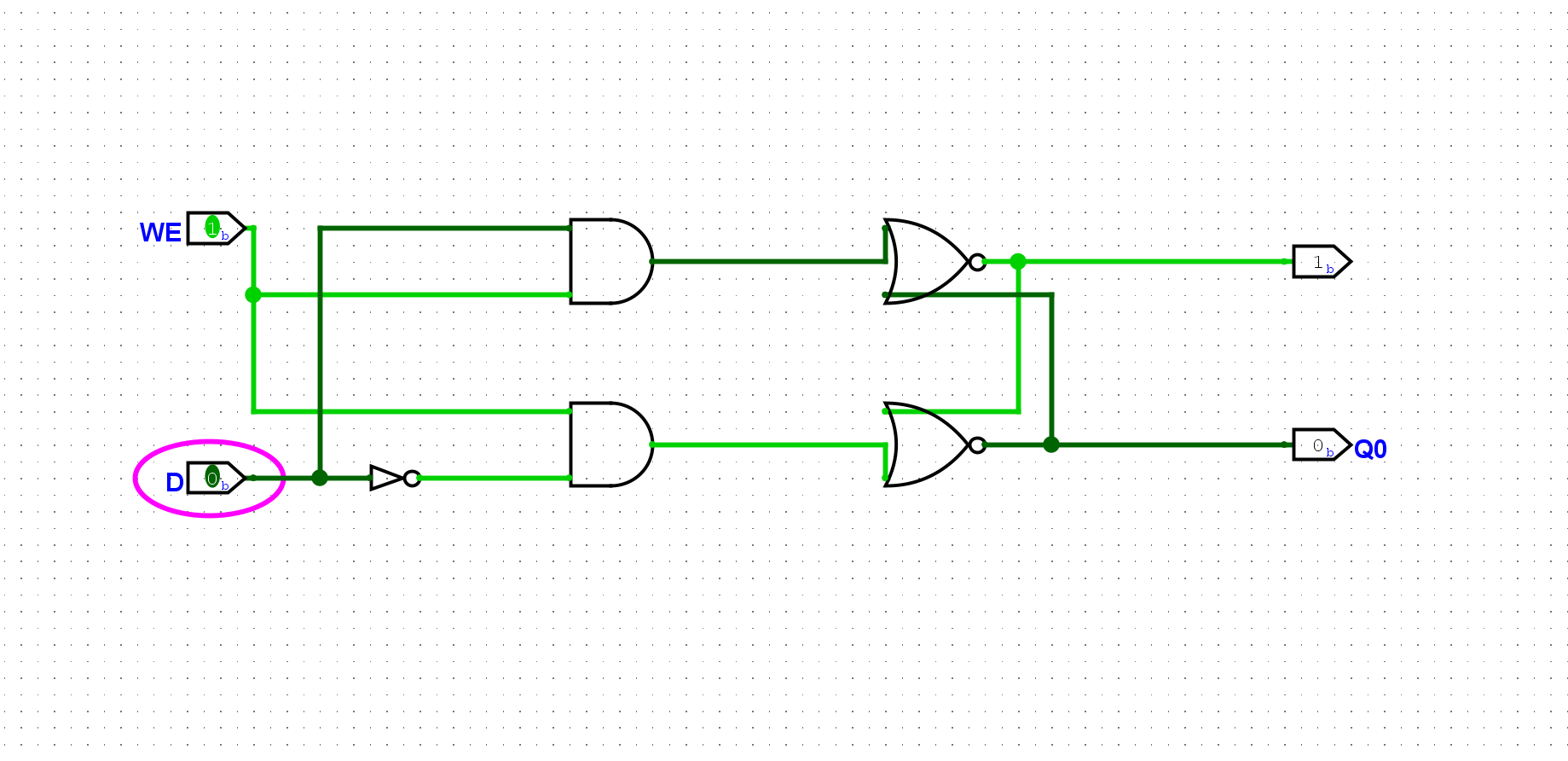
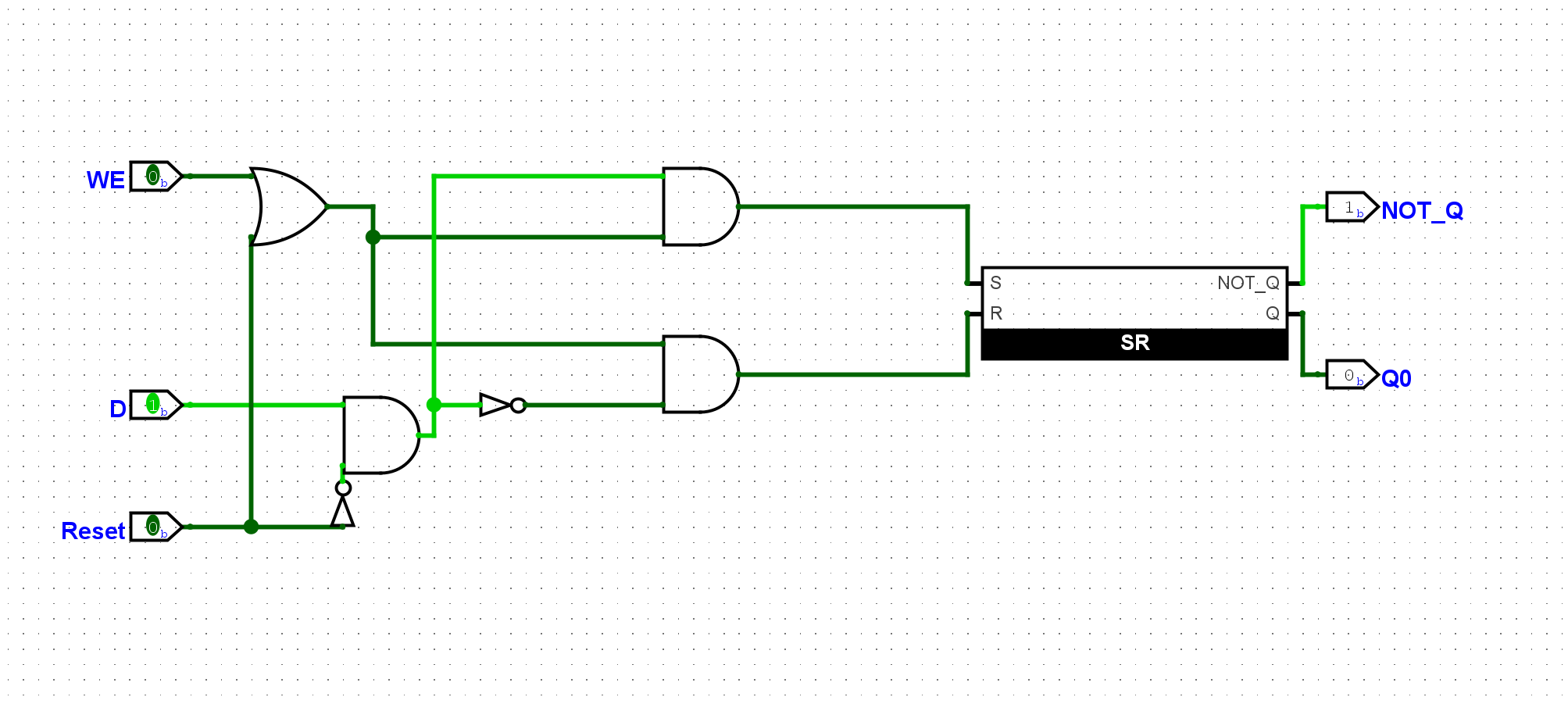
尝试为D锁存器添加一个用于复位的输入端和复位功能. 当复位信号有效时, D锁存器中存放的值将变为
0.
设置一个Reset信号,当Reset信号触发时,写入数据0就好了。
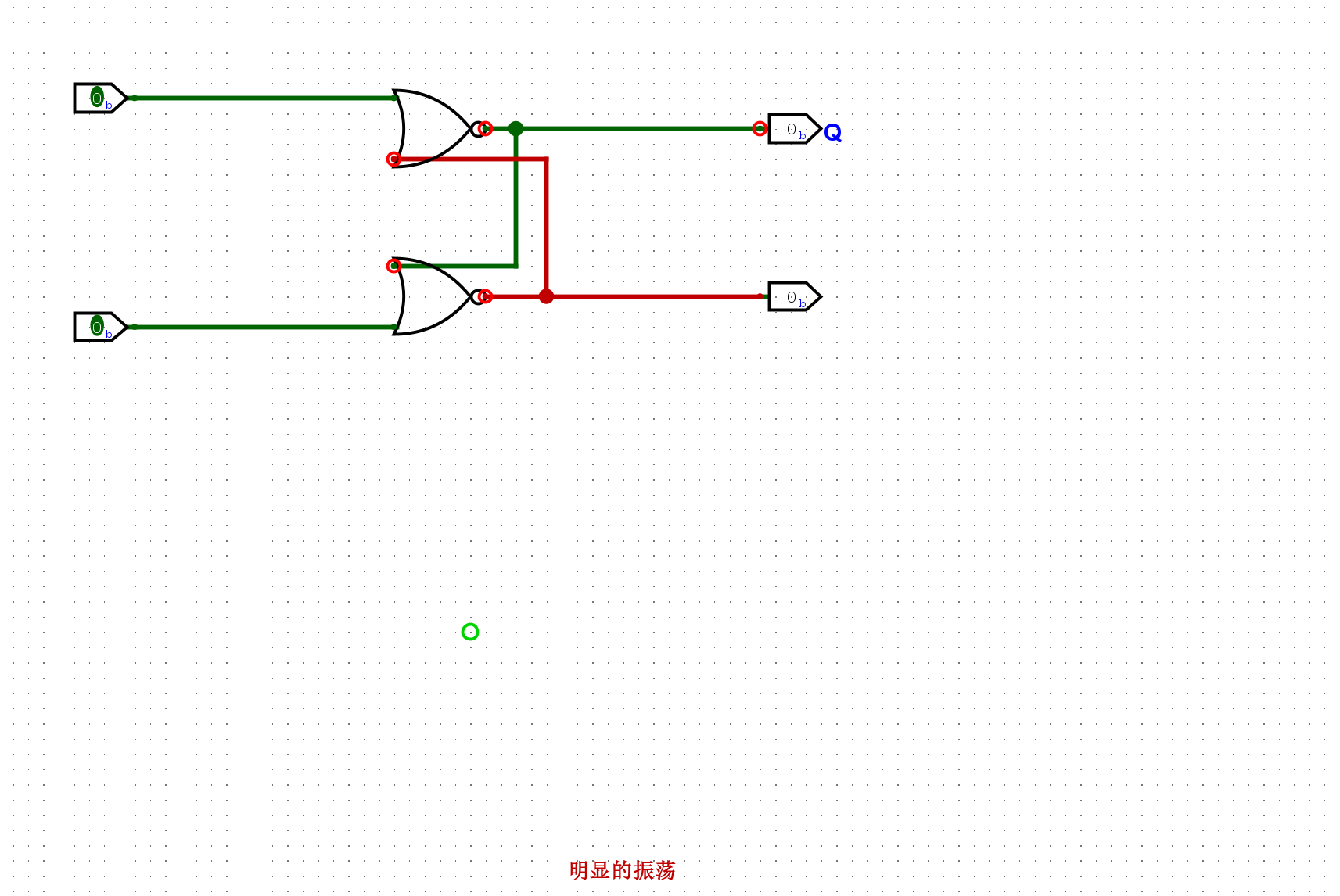
实例化一个带复位功能的D锁存器, 并将其输出取反后作为输入. 我们预期看到D锁存器的输出将在
0和1之间反复变化, 但你应该在仿真过程中看到Oscillation apparent的信息, 请分析原因.
由于循环依赖的问题输入数据D和输出Q此时应该是高频闪动的现象,但是仿真器无法模拟这个环节,所以会报错明显的震荡
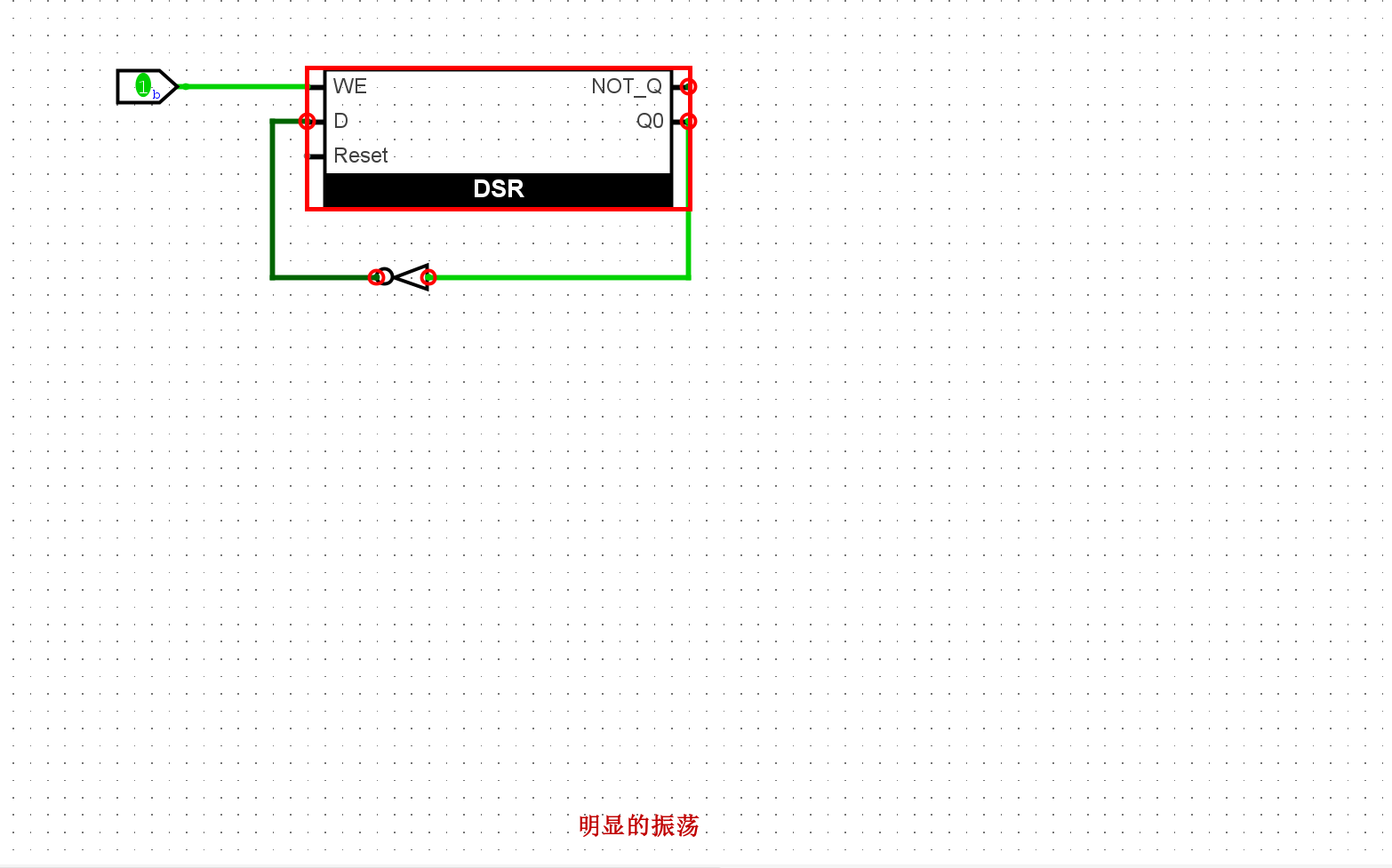
尝试在Logisim中通过门电路搭建一个D触发器. 搭建后, 将时钟端口与一个按钮相连, 按钮的按下和释放分别会产生高低电平, 因此点击一次按钮可产生一个脉冲, 以此来充当时钟信号. 尝试长按按钮, 来观察主从式D触发器的工作过程.
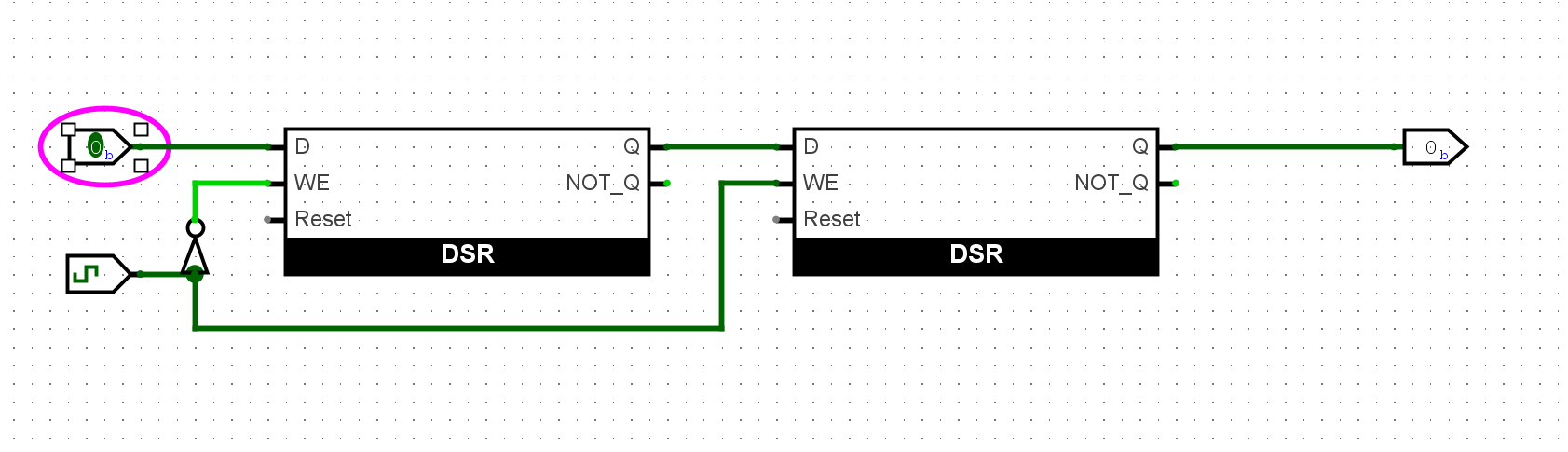
尝试为D触发器添加一个用于复位的输入端和复位功能. 当复位信号有效时, D触发器中存放的值将变为
0.
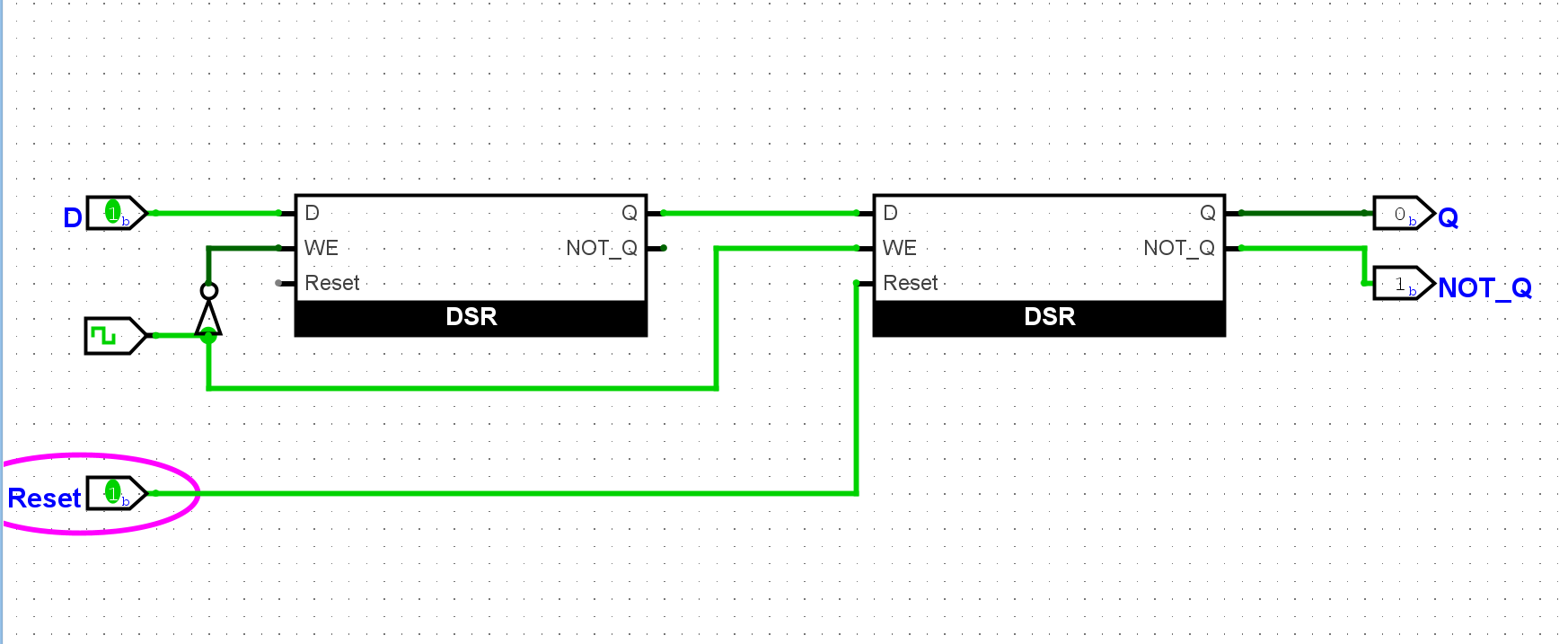
实例化一个带复位功能的D触发器, 并将其输出取反后作为输入. 我们预期看到D触发器的输出将在
0和1之间反复变化. 尝试和上文D锁存器的结果进行对比.
和D锁存器的结果不同,由于D触发器的存储只在时钟的上升沿发生改变,所以形成了有规律的振荡。
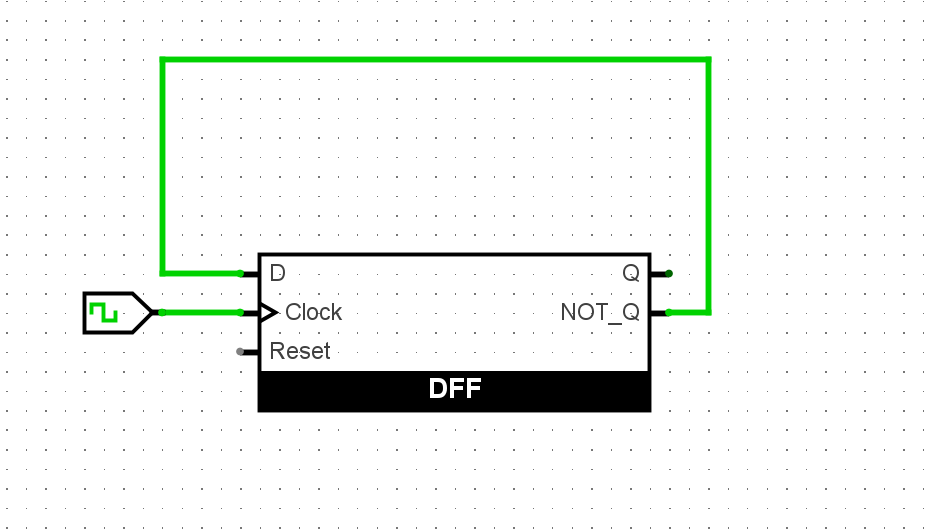
尝试在Logisim中通过D触发器和若干电路, 搭建一个带使能端的D触发器. 搭建后, 通过仿真检查你的方案是否正确.
也就是需要一个WE信号控制时钟的值是否有效,和reset的实现差不多,加个与门就好了:
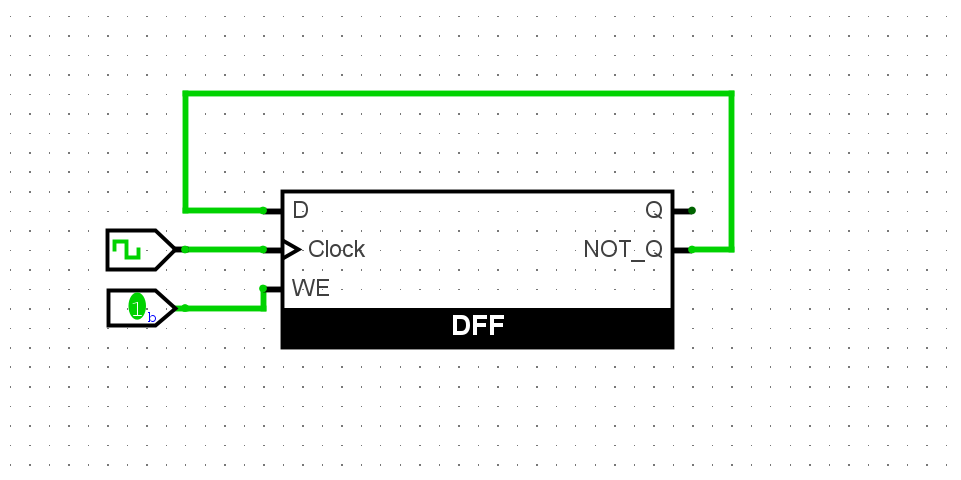
尝试在Logisim中通过D触发器搭建一个4位的寄存器, 具备复位功能. 搭建后, 尝试从拨码开关向寄存器写入4位数据, 并将寄存器的输出接到七段数码管进行显示.
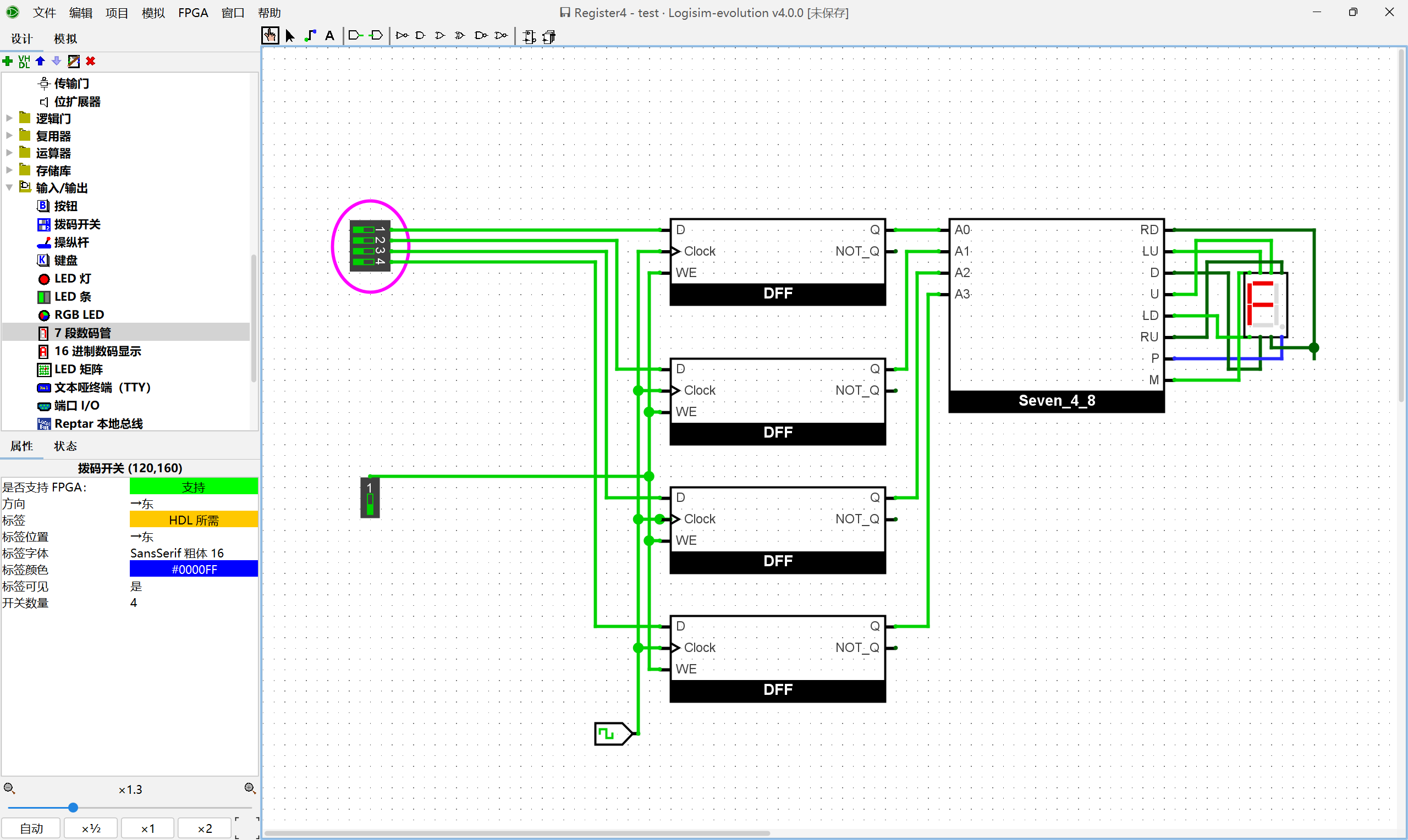
通过上述4位寄存器和之前搭建的加法器, 实现一个4位计数器, 每次时钟到来时, 寄存器中的值加1, 加到最大值时重新从
0开始. 在Logisim中, 你可以通过元件库中的Wiring(线路)类别下的Constant(常数)元件实例化一个常数, 具体使用方式请RTFM.
有点像D触发器的反转,只不过每次需要自增一次在输出值:
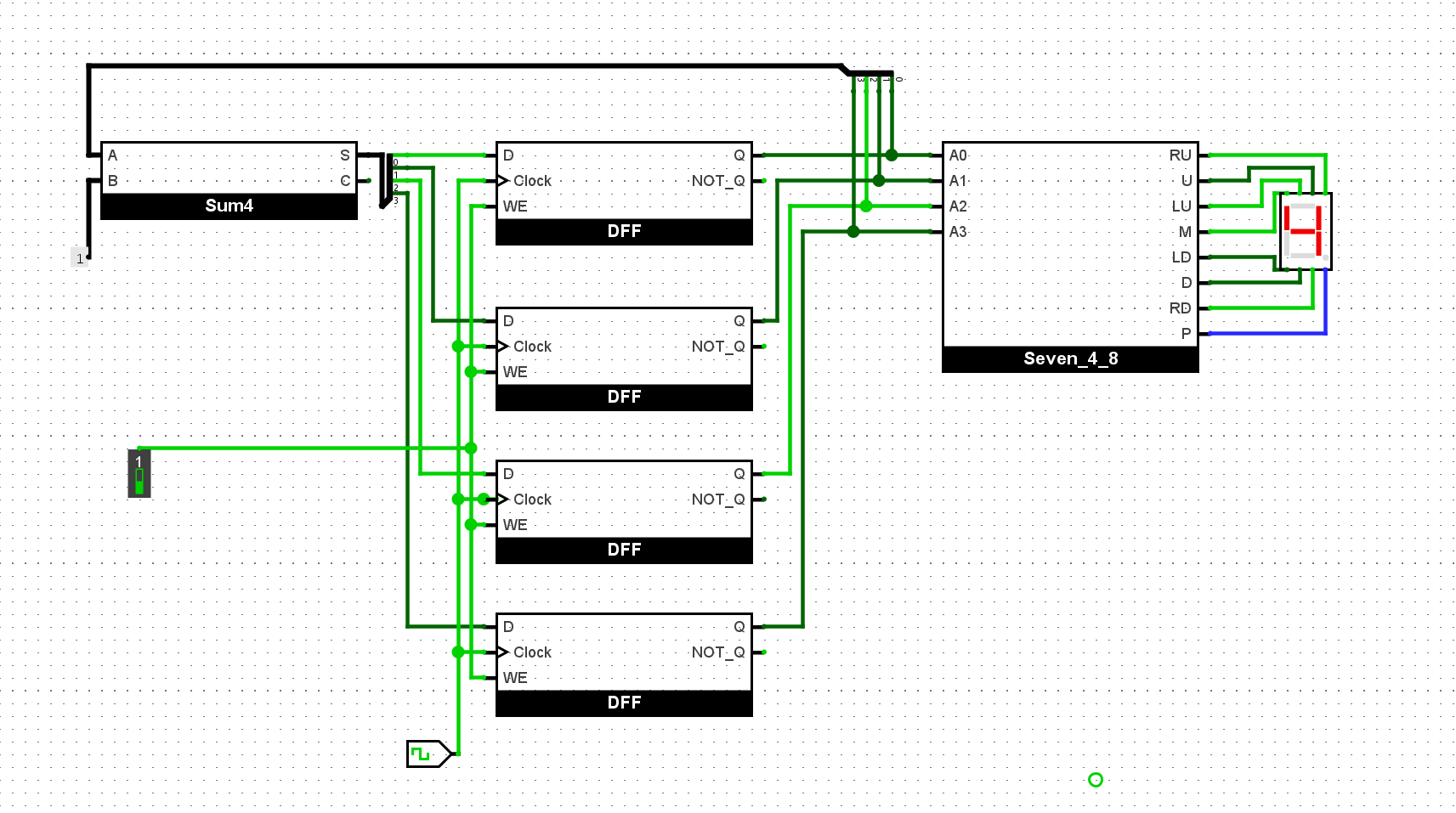
尝试通过寄存器和加法器, 计算出
1+2+...+10的结果. 为了容纳计算结果, 你可以考虑实现8位的寄存器和加法器.
使用两个寄存器,一个寄存器自增提供加数;另一个寄存器累加作为累加器:

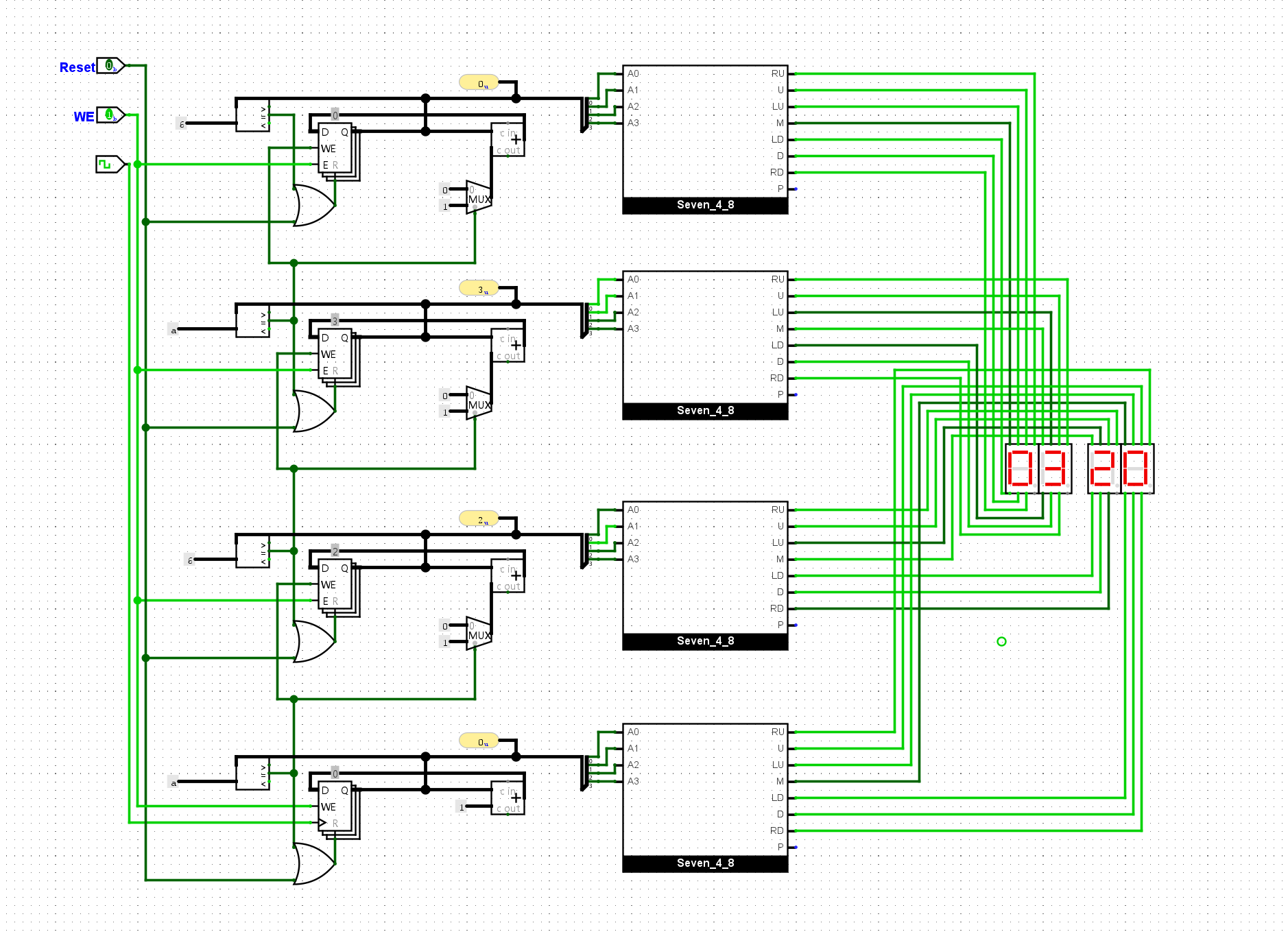
利用寄存器和七段数码管, 实现一个电子时钟, 具备”分”和”秒”的功能.
因为时序问题卡了好久
寒假报名了一生一芯的训练,作为对我这个学期的知识的一个补全,顺便学一些新的知识。为下个学期研究二进制安全做一点准备。这一部分就记录我在学习过程中的一些心得体会。就不再像往常一样讲的那么详细了,因为知识点在文档中给的很清楚,没必要再敲一遍。
主要认识两种类晶体管:

尝试分析以下门电路的行为和功能.
基于mos管,我们可以实现基础的门电路,我们分析下面的门电路功能:

只有A和B均为低电压时,才能输出高电平信号。当A或B任一处于高电压时,输出低电平信号。分析为——NOR门
尝试画出或门的晶体管结构.
画出或门的晶体管结构,就是在上面的基础上加上一个非门的晶体管结构就好了:
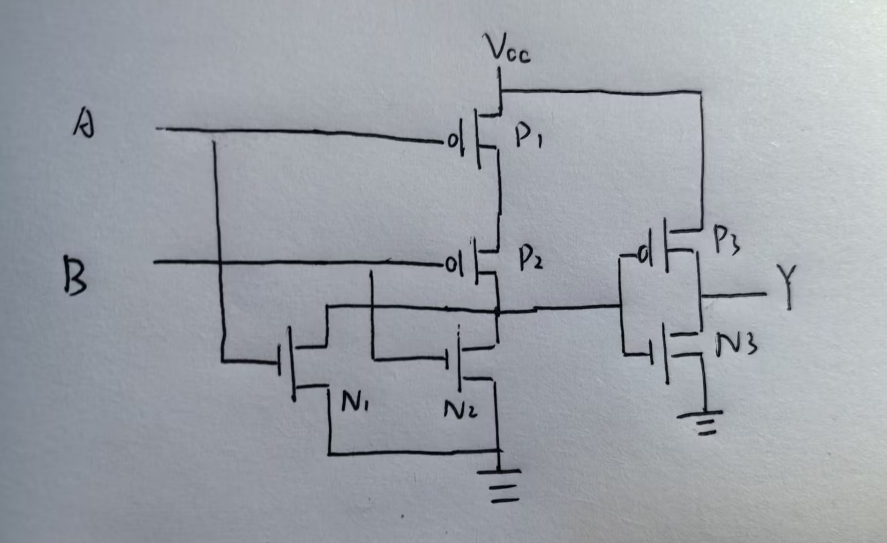
不难分析, 上述晶体管结构同样实现了三输入与非门的功能. 尝试对比两种实现方式中所需晶体管的数量.
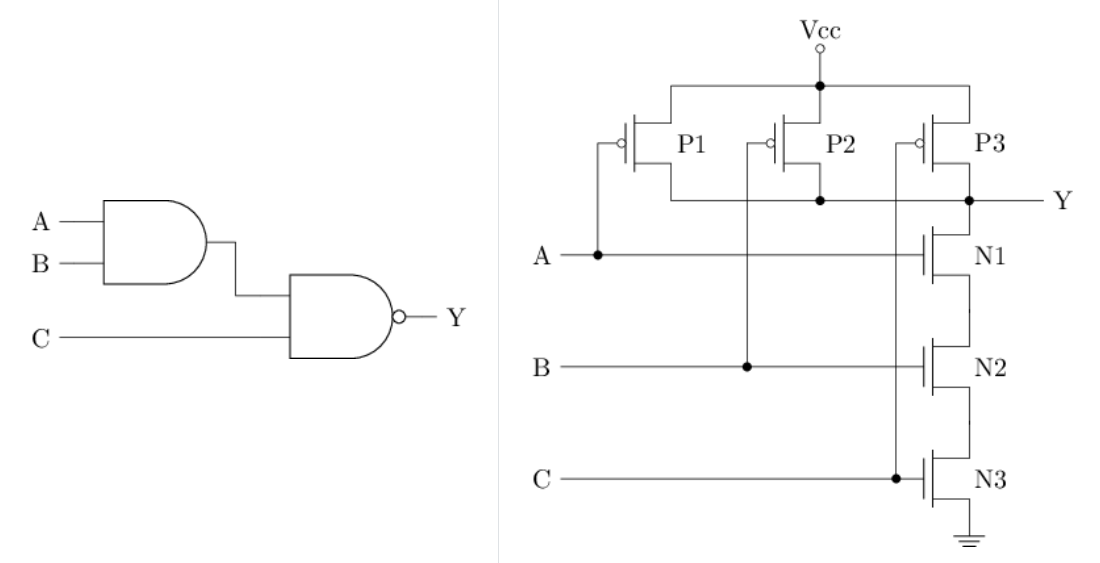
分别对两种方案进行计算:
1 | // 门电路方案 |
尝试在Logisim中用上文提到的门电路搭建一个异或门. 搭建后, 通过仿真检查你的方案是否正确.
实现正确后, 计算你的方案使用了多少个晶体管.
异或门的真值表,也可以看作是或门和与非门的交集。根据这个特征我们可以通过以下形式实现异或门:
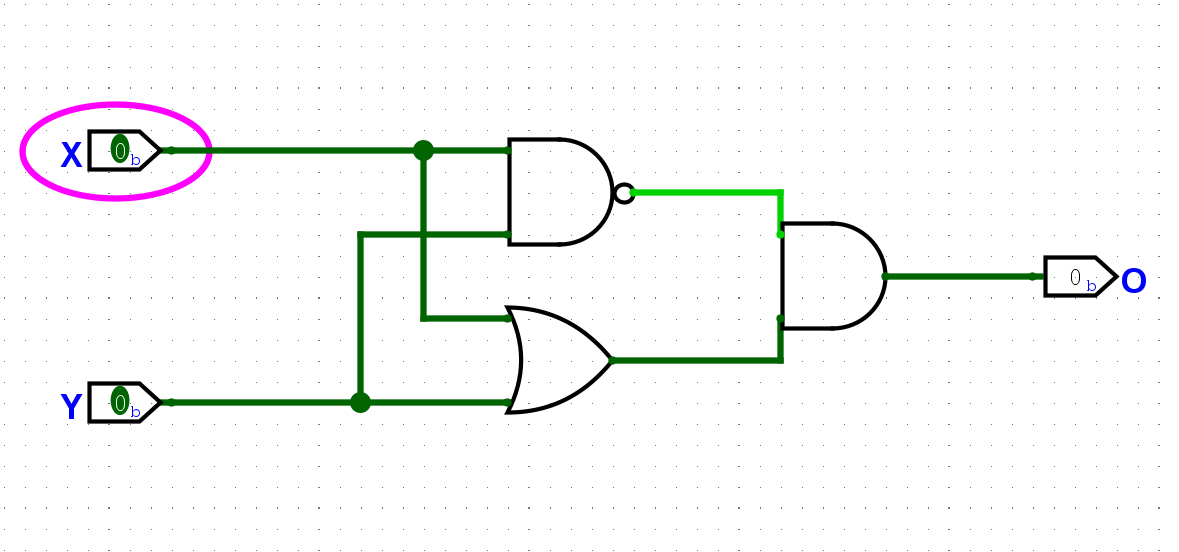
还有另一种操作是”同或”操作, 当输入A和B相同时, 结果为
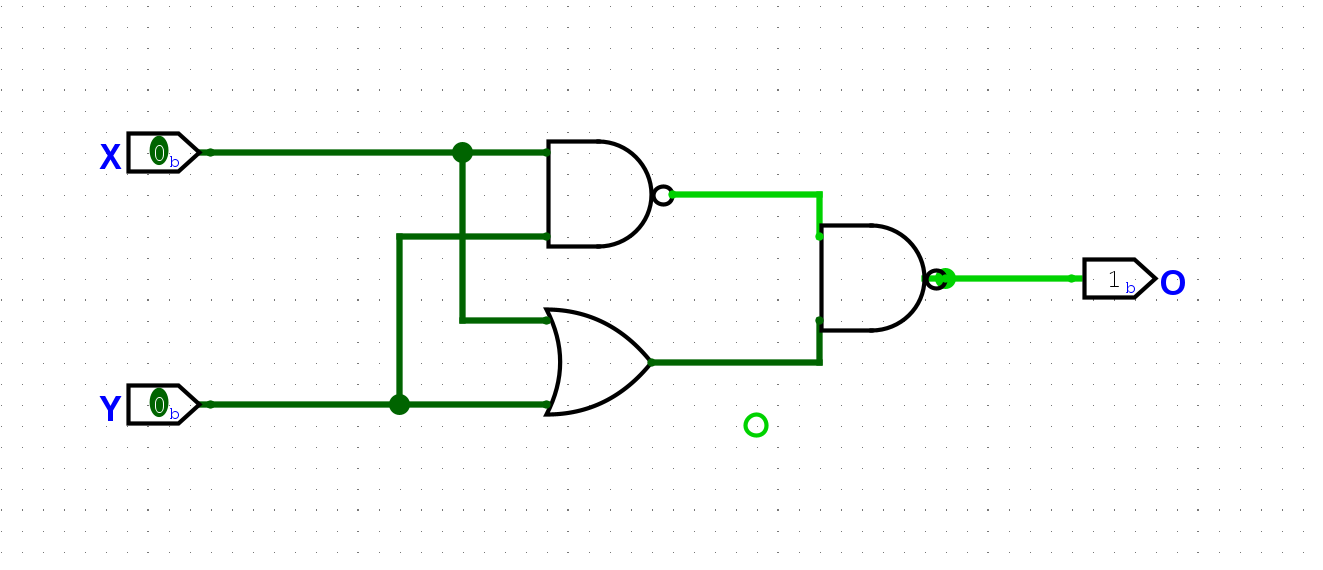
1, 否则为0. 同或操作可以认为是异或操作结果的取反.尝试在Logisim中用上文提到的门电路搭建一个同或门. 搭建后, 通过仿真检查你的方案是否正确.
在上面的基础上加一个非门就行了:
主要讲了2,10,16进制间的转换,这个比较简单,暂时略过。
我们基于晶体管实现了门电路,现在我们将忽略晶体管的电气特性,将视角聚焦到门电路层面。在此基础之上,搭建各种基础的基础电路模块。
尝试在Logisim中用门电路搭建一个2-4译码器, 它有2位输入, 4位输出. 搭建后, 通过仿真检查你的方案是否正确.
Logisim中也直接提供了译码器等现成的元件, 但我们还是要求大家使用门电路来搭建它们, 从而更好地学习数字电路的基本原理.
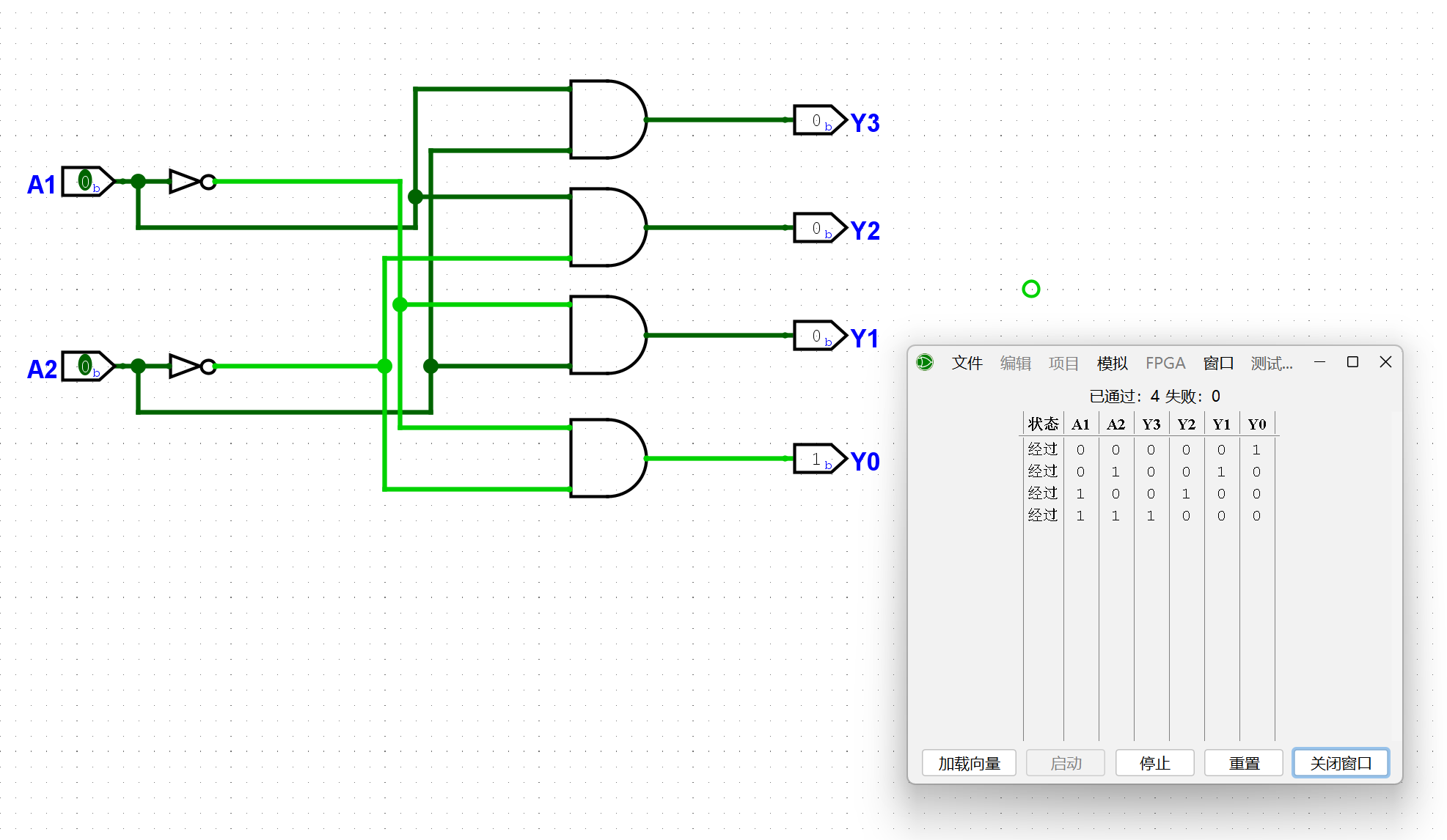
译码器在后续的数字电路设计中会经常用到, 为了避免用户重复设计相同的电路, Logisim提供了子电路功能, 相应电路只需要设计一次, 后续即可反复实例化. 具体操作方式请阅读官方手册中的
Subcircuits(子电路)部分.学习如何使用Logisim的子电路功能后, 尝试将你设计的译码器封装成子电路.
可以通过添加电路,然后设置好IO引脚,这样就可以打包成一个子电路,方便之后调用:
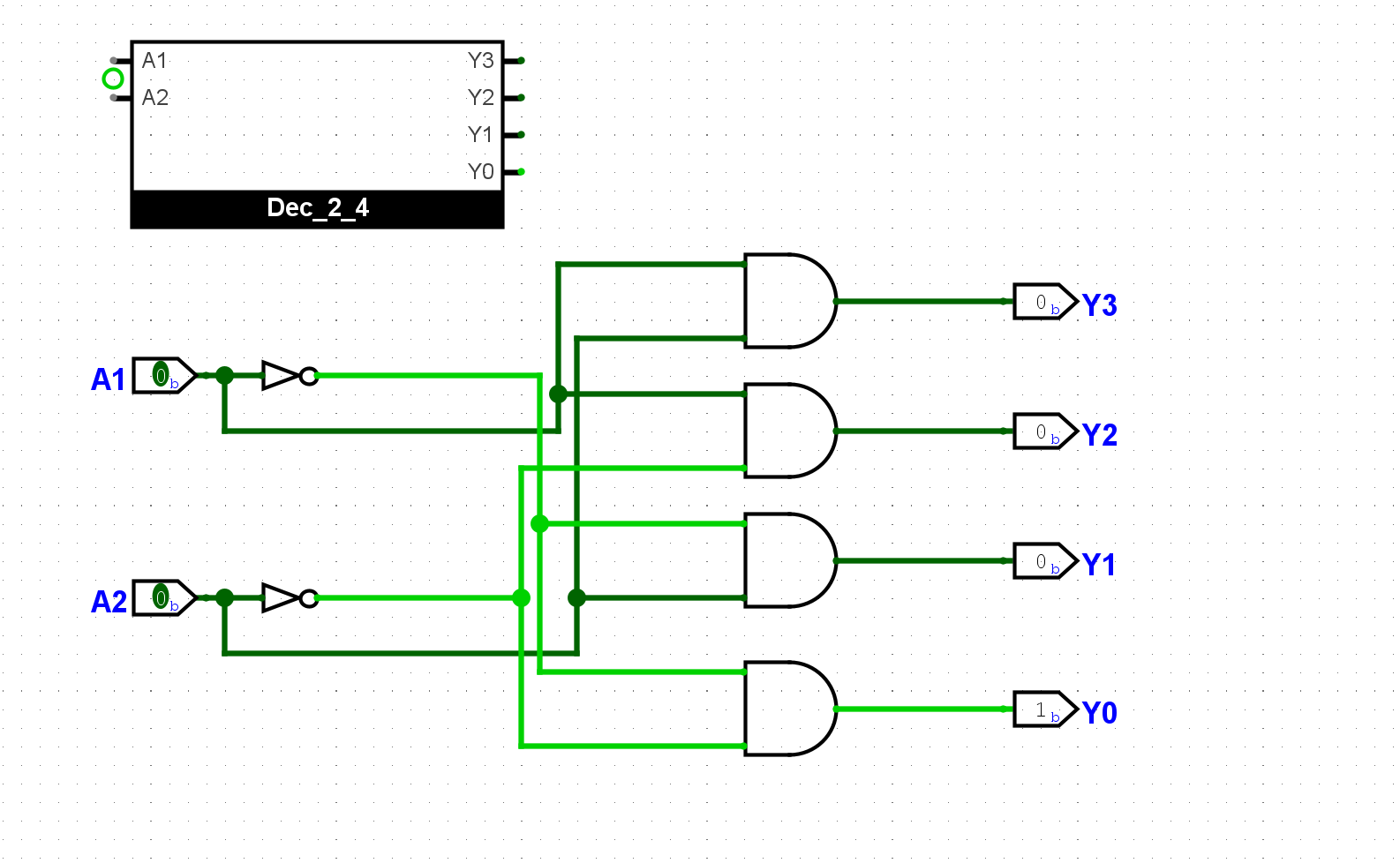
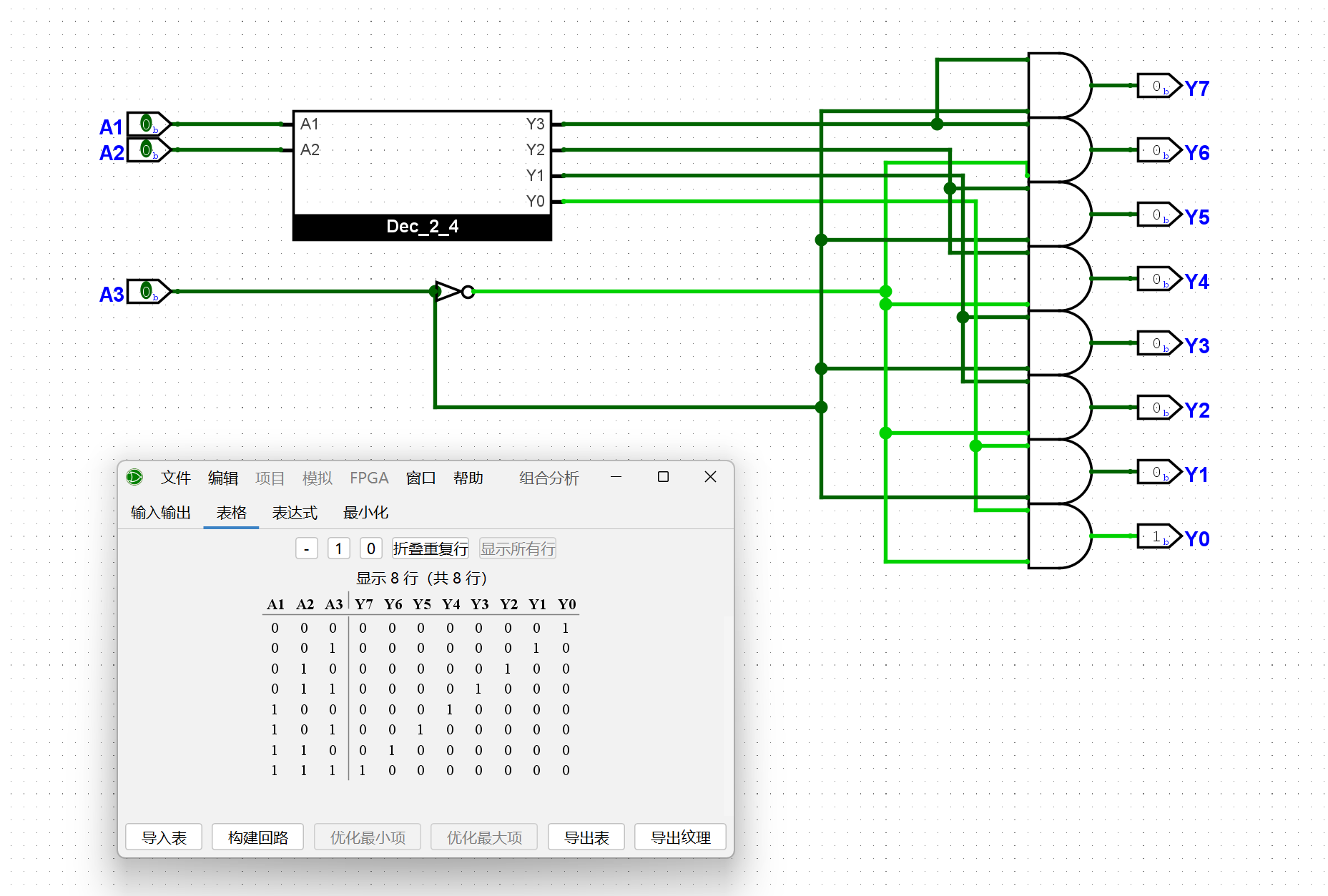
3-8译码器有3位输入, 8位输出. 尝试实例化若干个2-4译码器(具体数量交给你的思考), 并添加少量门电路, 从而实现3-8译码器的功能. 搭建后, 通过仿真检查你的方案是否正确.
通过第三个信号和原有的2-4译码器,实现3-8译码器
尝试在Logisim中通过门电路搭建一个七段数码管译码器, 它有4位输入和8位输出, 分别与拨码开关和七段数码管相连. 七段数码管译码器支持十进制数字的显示, 即当输入对应0-9时, 七段数码管显示对应的数字; 对于其他输入, 七段数码管只显示小数点. 搭建后, 通过仿真检查你的实现是否正确.
这里用了隧道和解码器,来简化实现,对着文档搓就行了。RTFM!!!
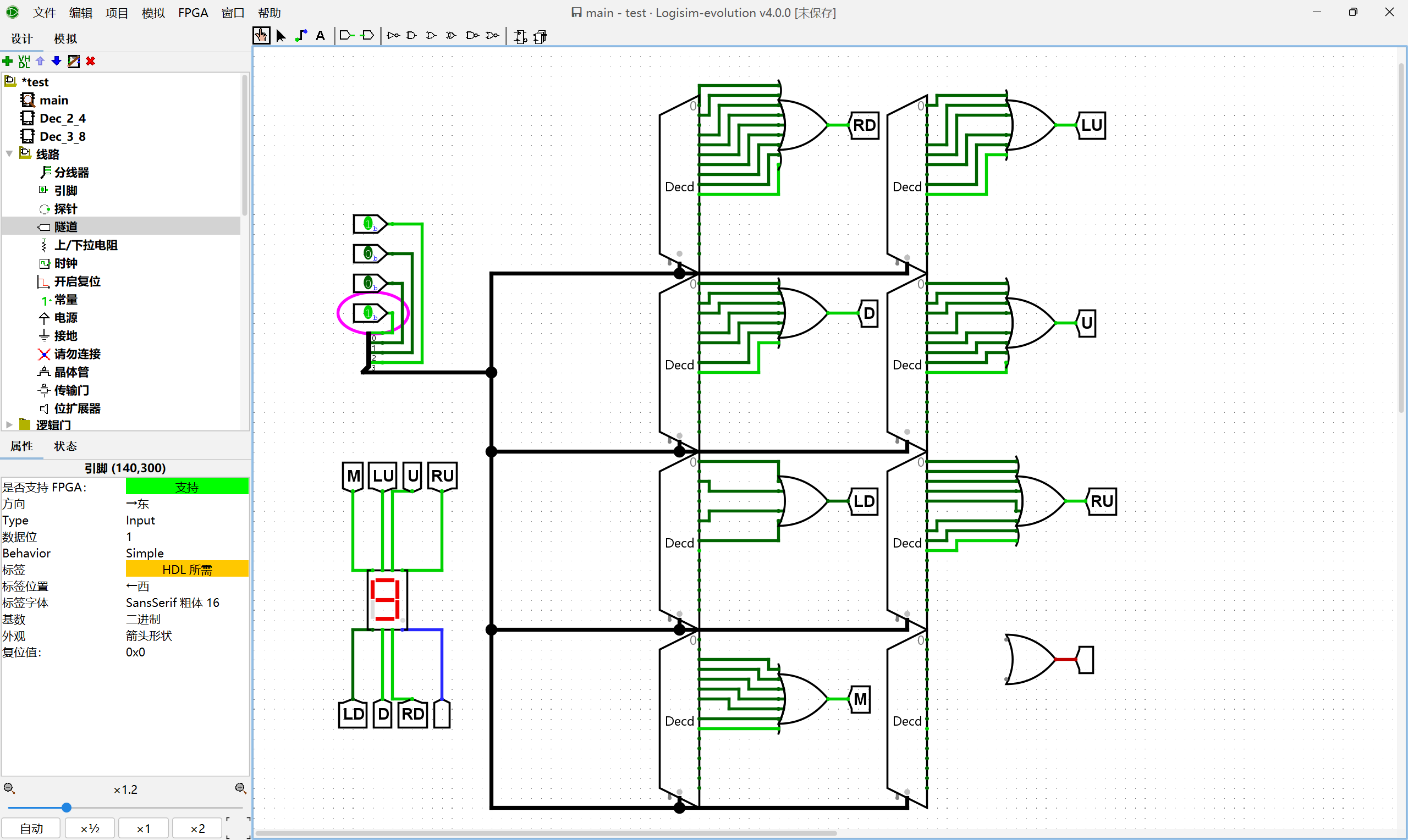
尝试在Logisim中通过门电路搭建一个支持十六进制数字的七段数码管译码器. 和上述的十进制数字相比, 当输入对应10-15时, 七段数码管分别显示A, b, C, d, E, F. 搭建后, 通过仿真检查你的实现是否正确.
在上一个的基础之上添加对A,b,C,d,E,F的数码管支持就好了。就是有点麻烦。
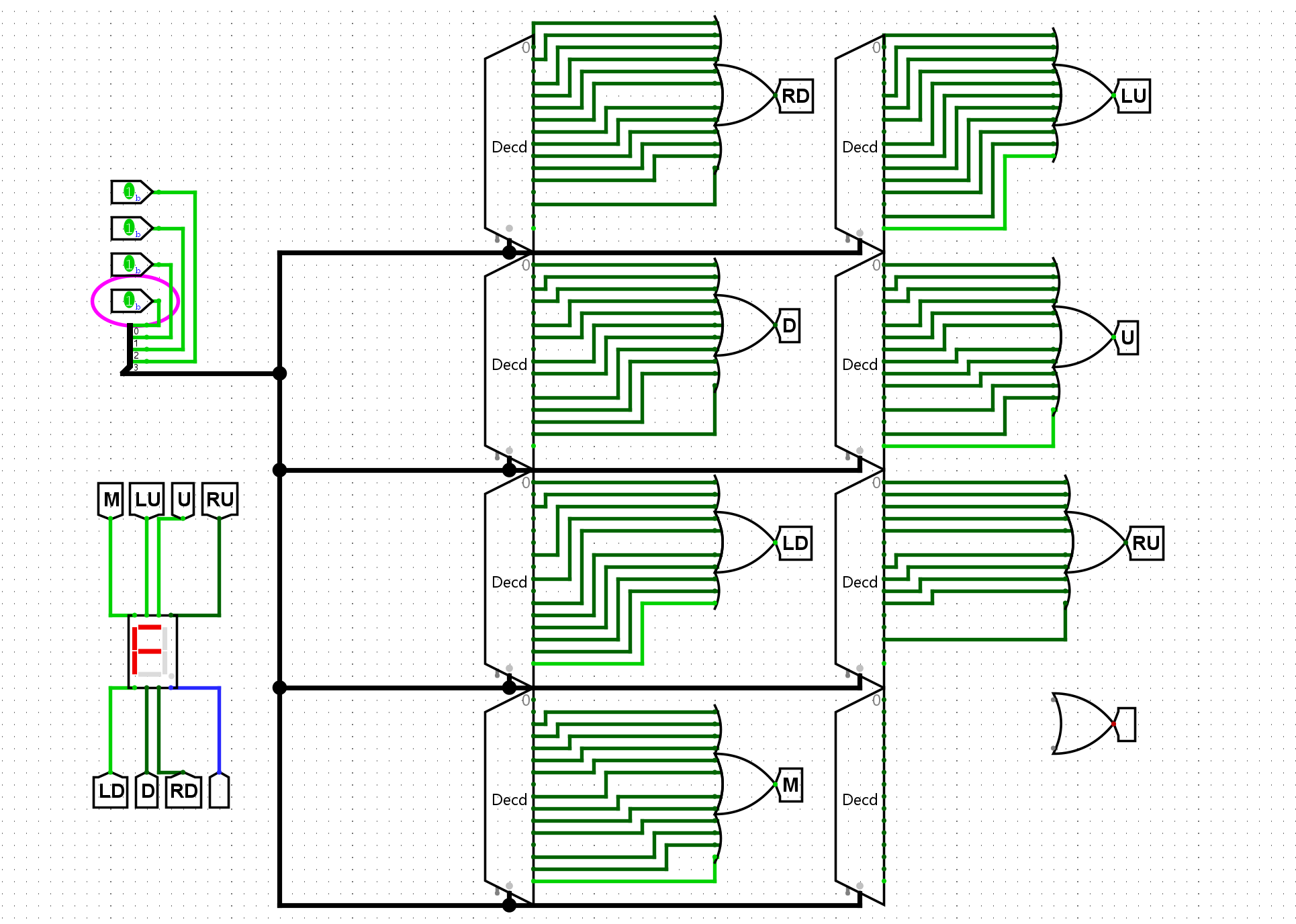
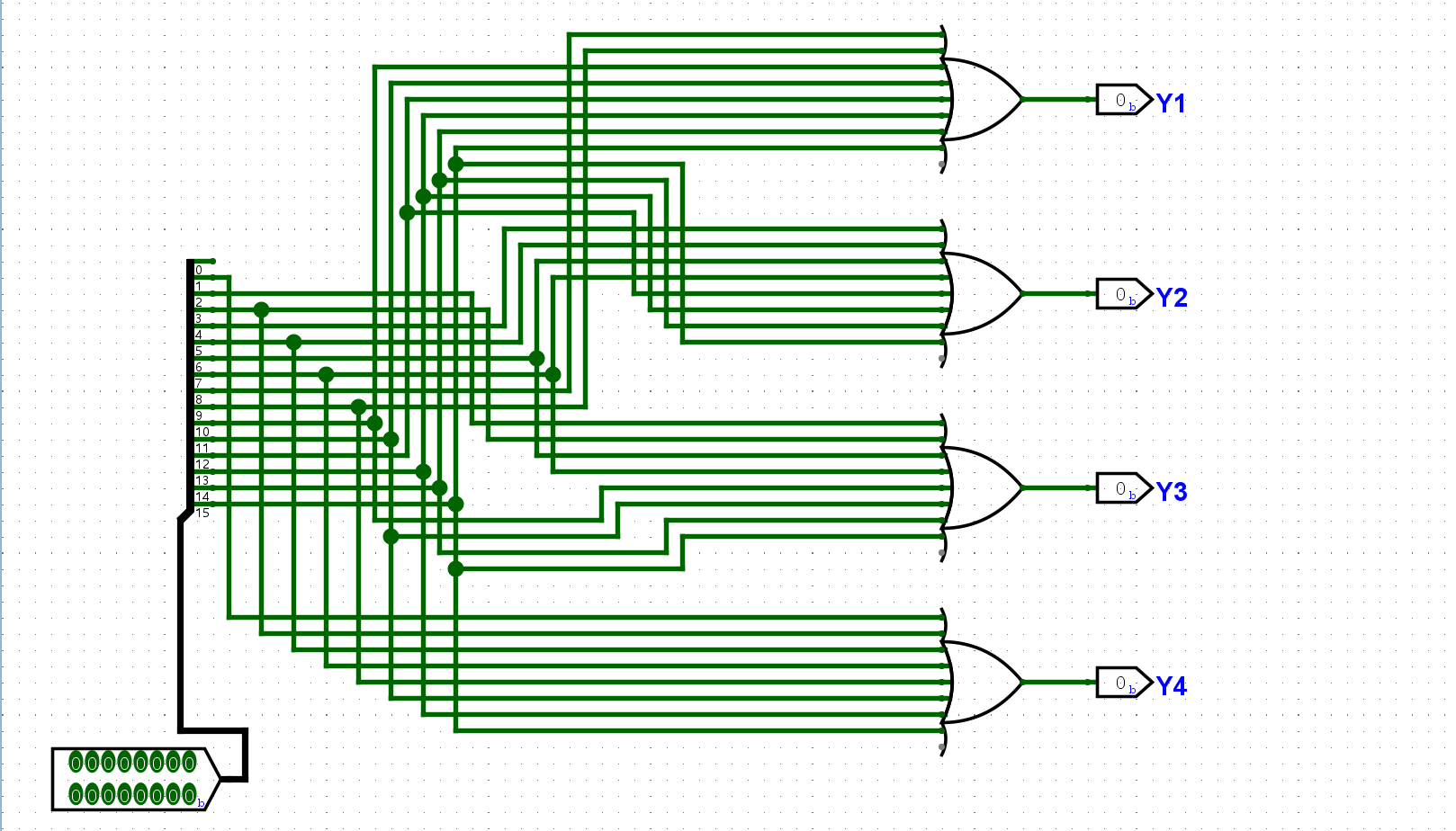
尝试在Logisim中通过门电路搭建一个16-4编码器, 它有16位输入和4位输出, 分别与拨码开关和七段数码管译码器相连, 使得编码器的输出结果通过十六进制数字显示在七段数码管中. 搭建后, 通过仿真检查你的实现是否正确.
每个Y的输出只关注当前的二进制对应的位数是否需要Y,然后使用或门进行合并:
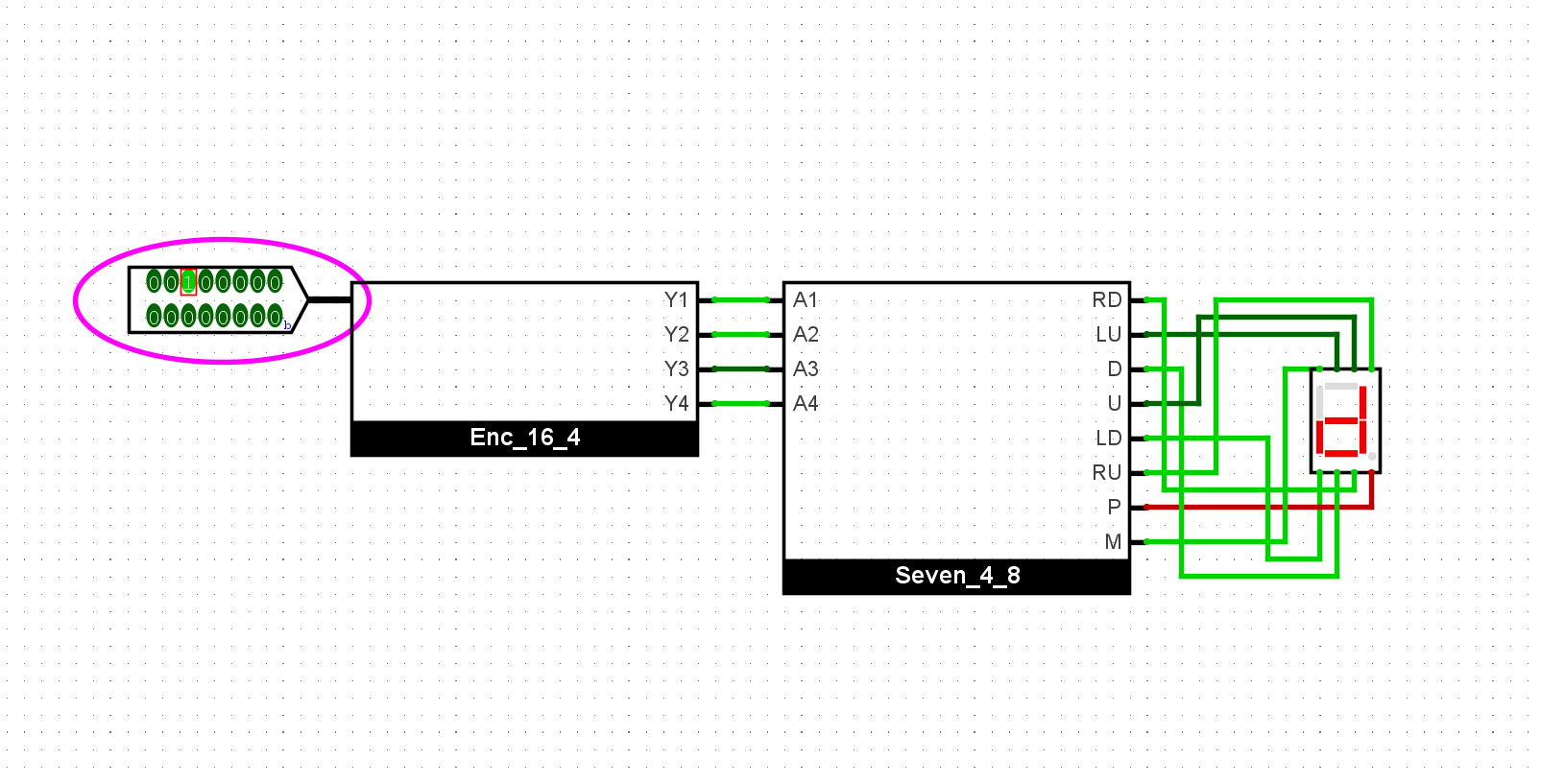
使用封装的译码器驱动我们的七段管:
根据上述真值表, 尝试列出每一位输出的逻辑表达式. 然后尝试在Logisim中通过门电路搭建一个4-2优先编码器. 搭建后, 通过仿真检查你的方案是否正确.
实现后, 对比4-2编码器和4-2优先编码器所需的门电路数量.
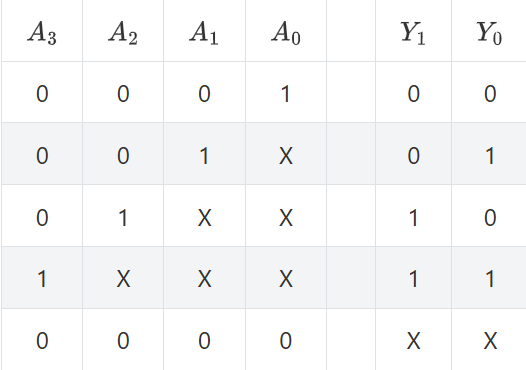
image.png
实现的过程中发现只有当A2为1时,后面的A1信号会对结果造成影响。设置一个与门作为开关就可以抑制这个现象了:
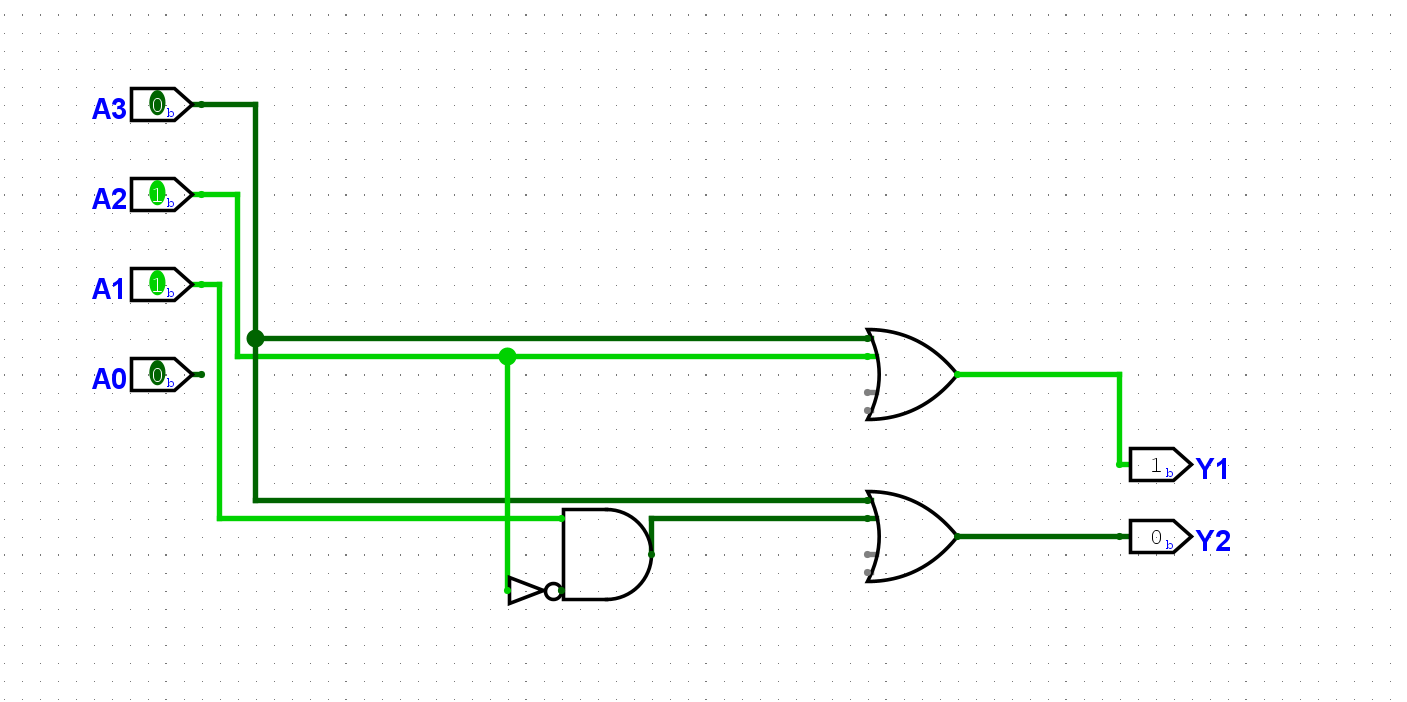
门电路数量比较:
1 | // 4-2 |
尝试在Logisim中通过门电路搭建一个1位2选1选择器. 搭建后, 通过仿真检查你的方案是否正确.
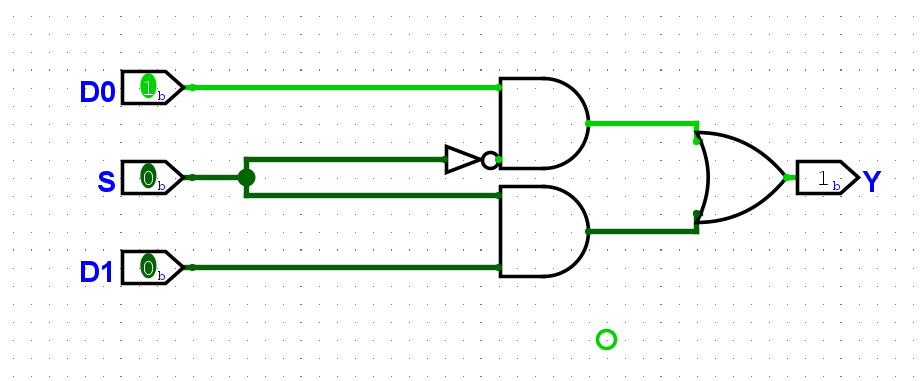
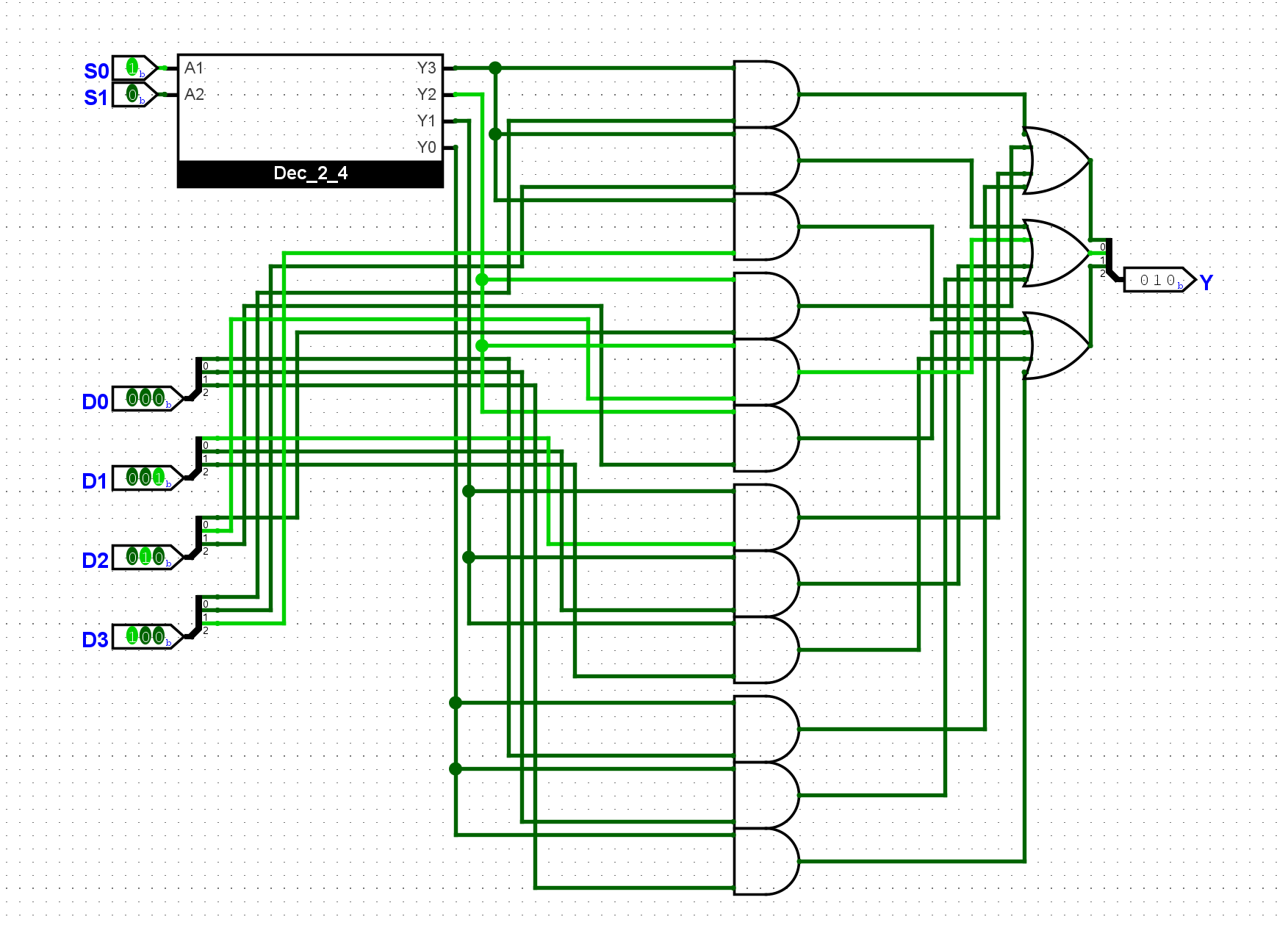
尝试画出3位4选1选择器的电路结构图, 然后在Logisim中通过门电路搭建一个3位4选1选择器. 搭建后, 通过仿真检查你的方案是否正确.
这个比较复杂,但是原理一样:
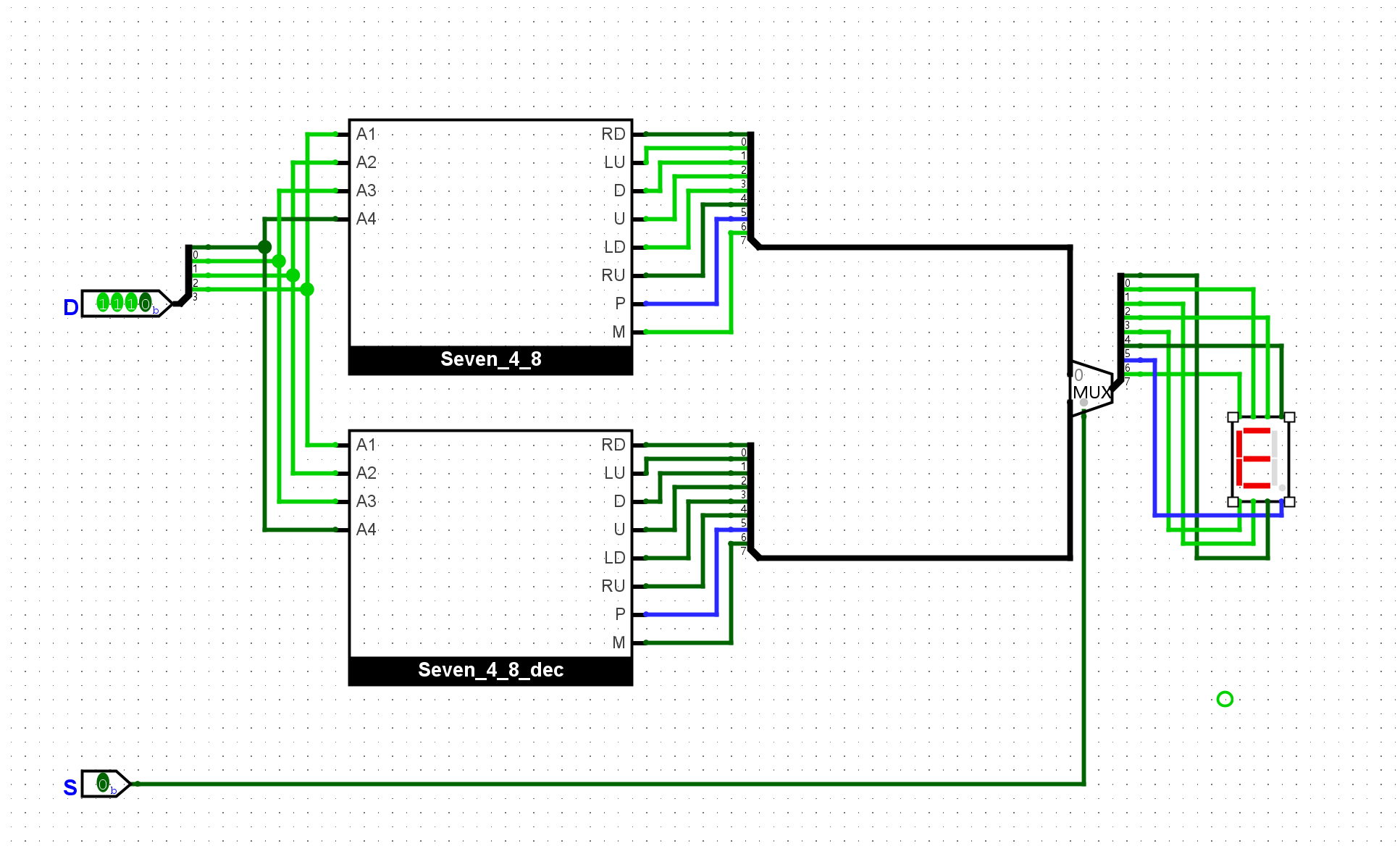
通过5个拨码开关和1个七段数码管, 实现如下功能: 其中4个拨码开关当作数据输入, 剩下1个拨码开关作为进位计数制的选择, 当选择信号为
0时, 七段数码管以十进制方式显示数据; 当选择信号为1时, 七段数码管以十六进制方式显示数据. 在输入数据为10-15时, 两种显示方式有所不同.
使用系统封装好的多路复用器就很容易实现
尝试在Logisim中通过门电路搭建一个4位比较器, 然后通过两组拨码开关对比两组数据是否相等, 若相等, 则点亮一个LED灯. 搭建后, 通过仿真检查你的方案是否正确.
四个同或门比较信号,然后使用与门收集信号,若全为真则各位相同:
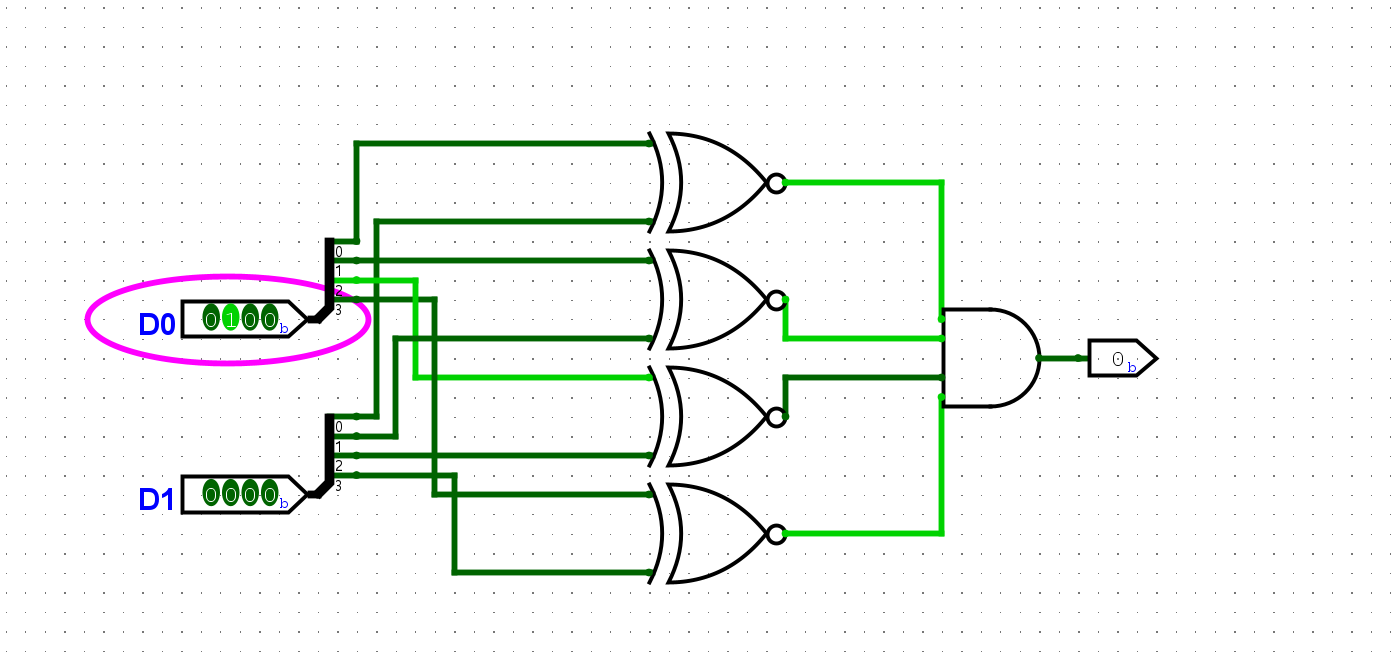
尝试列出1位全加器的真值表, 并在Logisim中通过门电路搭建一个1位全加器. 搭建后, 通过仿真检查你的方案是否正确.
本质上就是在半加器的基础上,对一个新的进位进行额外的判断:
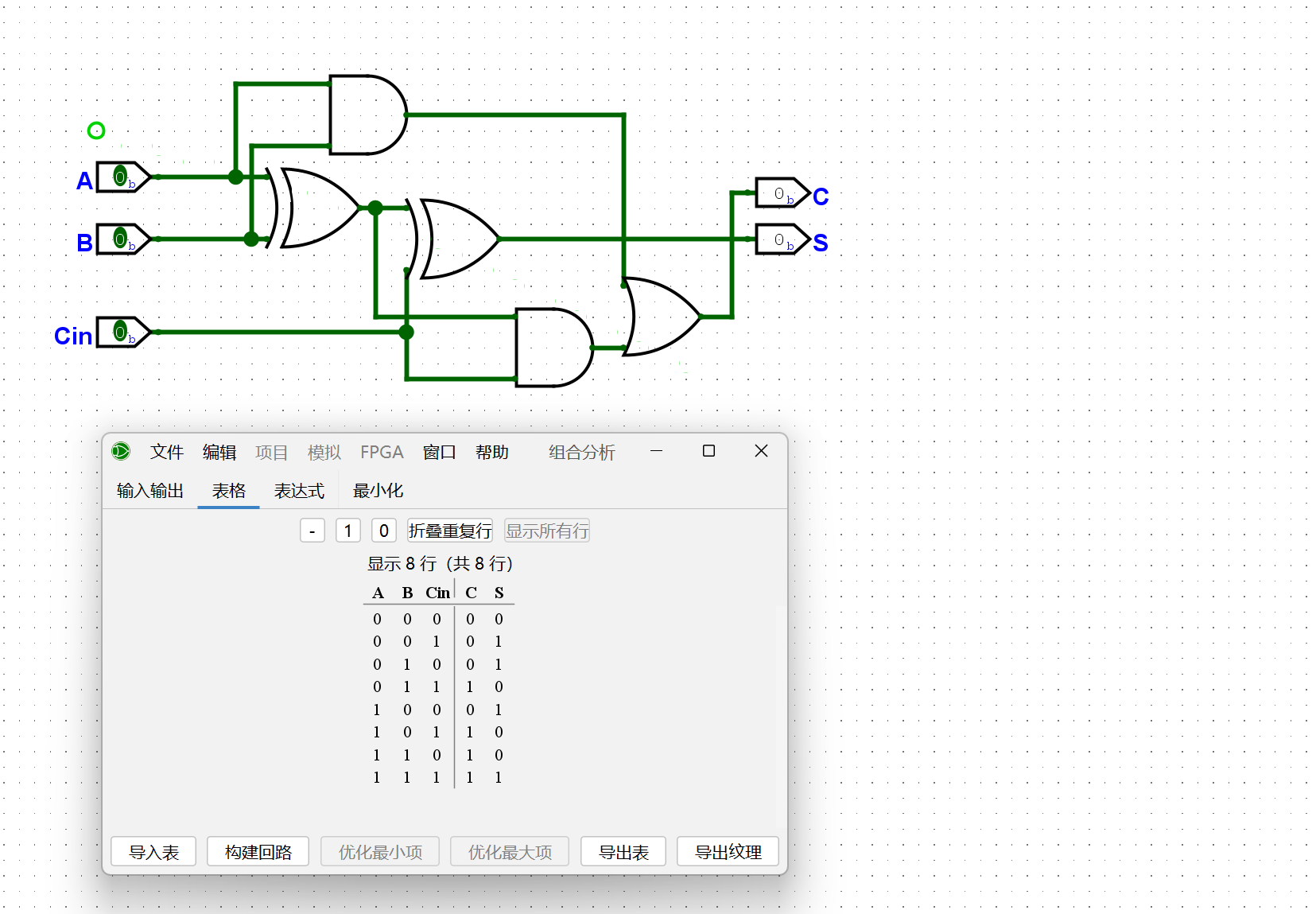
尝试实例化若干个半加器, 并添加少量门电路, 从而实现一个1位全加器. 搭建后, 通过仿真检查你的方案是否正确.
一样的原理,只不过封装了起来
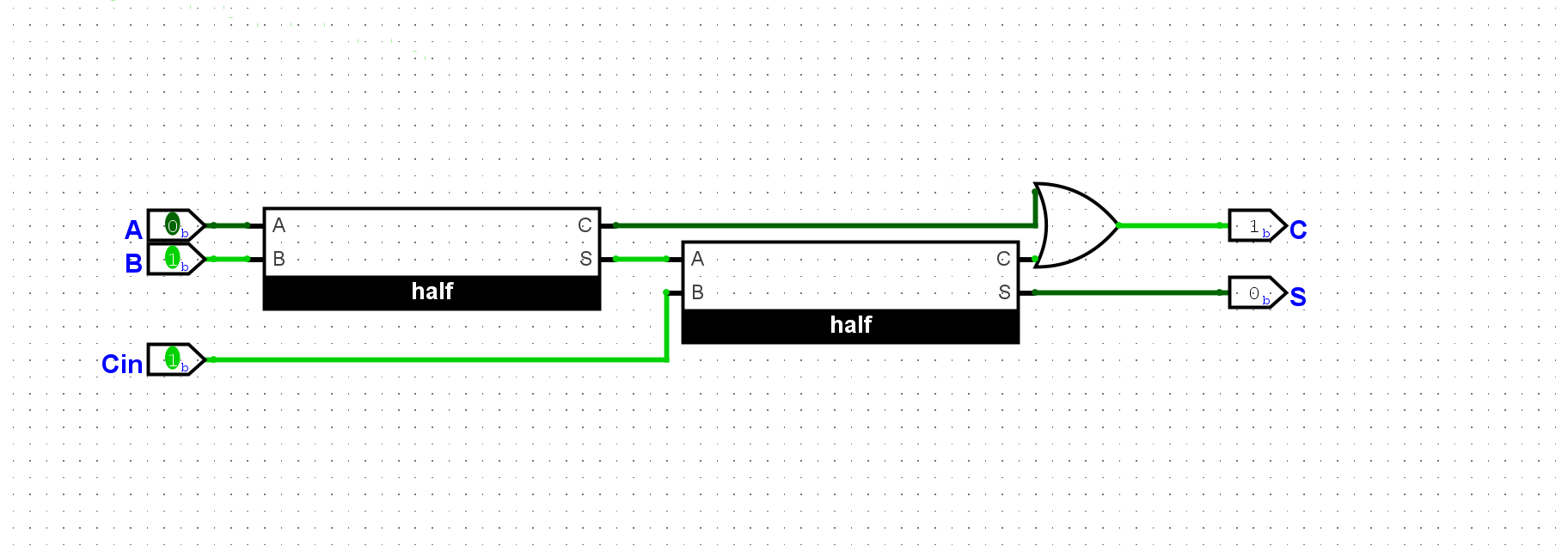
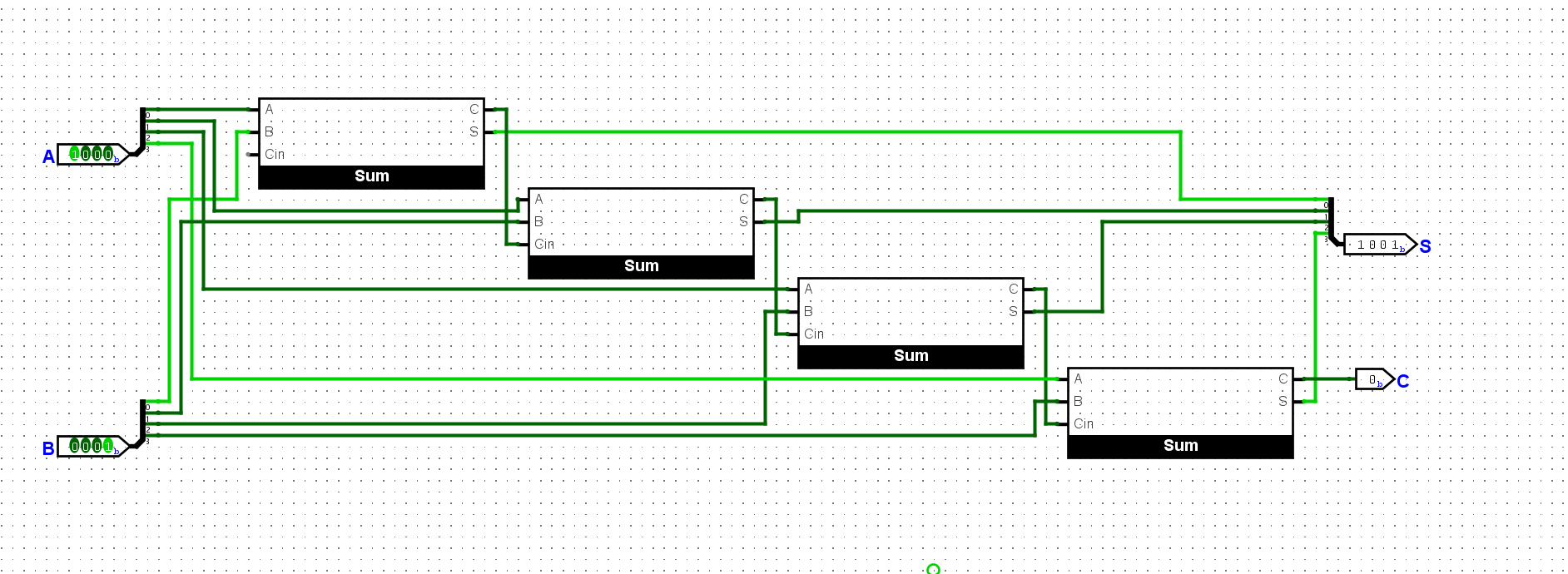
尝试在Logisim中通过门电路搭建一个4位加法器, 用七段数码管按十六进制显示加法器的两个输入和结果, 并用一个LED灯指示加法结果是否产生进位. 搭建后, 通过仿真检查你的方案是否正确.
使用全加器串联起来:
终于考完试了,也要做好打算琢磨一下接下来该做什么了。总体来说,这个寒假会好忙,但是也是一个很好的机遇。我打算用这段时间好好提升一下自己,无论是学习上还是生活上。
先对我的一月份做个小小的反思吧,这个月主要是期末周,导致我都没有更新博客,也没有学什么新的技术,寒假我会好好补起来的。至于期末开始,只能说考的一般吧,自己还是抱有侥幸心理,偷了很多懒。导致复习的过程很赶,很多知识都是一知半解。尤其是概率论,唉,基本都不会,我考前还一直在打游戏,也不知道怎么想的。
然后就是主要讲一讲寒假的安排吧,和往常一样,我想做的事情比较多,但是不一定能做到。但是目标还是要定下来的:
这些是要做的事情,我还想立几个比较具体的任务,我打算看完三本书:
所以综上所述,要做的事情还是很多的。所以每天要早睡早起,少刷视频。我发现这个学期我刷视频的时间明显变多了很多。
今年的寒假很长,希望能通过这个寒假给自己带来一点改变。不能止步不前,Keep on going。
2025年马上就过去了,这一年发生了很多事情,我也不怎么记得了。仔细一想感觉一年好长,但是时间却又过的好快。最近很多软件都公布了年度报告,不知道为什么我甚至不敢点开,我好害怕去回想这些事情。可能是因为最近过的不是很好吧,我不想去回忆以前很多很开心的瞬间。我怕自己看到了会难过。
但我还是点开看了,我最先意识到的就是,原来我有这么多时间。我仔细算了一下,人的一天有24个小时,去掉12个小时吃饭睡觉,我还剩下12个小时。一年下来就是 4380个小时,我的B站视频时长是930个小时,今年的游戏时长1500个小时。我将近一半的时间都在娱乐,我推测学习时长也就1000个小时。我的每一天无形之中浪费了很多时间。如果我能注意到这些时间就好了。
我总是觉得自己好忙好累,我为什么不拿这些多余的时间去陪陪自己的女朋友,或者锻炼培养下自己的爱好。
我觉得很自责,心里。我明明可以做得更好,但是我什么也没做,我感觉自己是个无聊的人,可能每天就是宅着,过完一天又一天。我总是觉得自己毫无长进,我现在知道这份感受的来源了。我希望新的一年自己能做的更好吧,心里非常难过,也不知道说什么好,我觉得还是挺后悔的,我十二月有一段时间什么也不想做。每天就是打游戏,看动漫,尽量让自己不去思考吧。我玩蔚蓝,把BC面全部通关了。我一直死一直重来,我心里是有幻想的,就好像我通关了之后我就能大声的宣告,自己从失恋的阴影中走了出来。但我还是没能做到,我不仅没有通关,也没有从失恋的阴影中走出来。
我看网上很多人说,走出失恋的痛苦就需要你把你的注意力转移到自己身上,去打破现有的僵局,去改正自己的不足。我觉得很有道理,但是太难了,失恋在我看来就是一种精神病,让失恋的人走出来,就好比让抑郁症开心一点。我也不知道该怎么做吧,只是尽量的让自己忙一点。最近开始着手准备期末和大作业的项目,所以心情好一点,暂时不会去想了。零散的时间我会看看国际象棋,看看视频。最近这几天稍微心情好一点。所以写下这篇反思。
但是这样的日子还要多久呢,我要一直让自己忙碌下去,什么时候才能停下来呢。-
尽管如此,我还是想像往常一样定下几个目标,尽力去做吧:
我觉得放弃确实狼狈,但是也不能因此丢失了再来的勇气,否则我也不再是我。通过这段时间我对自己的观察,我发现我有一个特点。无论是打游戏还是生活中,只要有一件我想做到的事情我就会没日没夜的去完成它,大部分时候我都能做到。少部分时候,我会遇到无论如何也无法解决的问题,我会情绪很失控,很自责,很消极。我不知道这样是好还是坏,但是我不愿意放弃,当下我应该整顿好自己,然后再来一次。不能止步不前。
也许这也是一次转机吧,这段时间我重新认识了自己,想了很多以前不会想的事情,希望我能做到越来越好。如果可以的话,我还是想去北京,去看北方的初雪。冬天如约而至,可是你成了我永远迟到的季节。我要完成我的遗憾。
找到一个比较好的项目Byterun,这里进行一下复现。
Byterun 是一个基于Python实现的Python字节码解释器,简化了Cpython的实现,展示了Python解释器在底层上的实现原理,以及相关的组织过程。
解释器本质上就是一个虚拟机,他会对你产生的字节码信息进行解释,然后基于栈运行,实现运算、分支条件、循环结构等功能。
Python解释器实际上就是一个字节码解释器,它接受字节码,然后输出运行结果。当你写下一段Python代码时,会被词法分析器解析为token流,然后通过语法分析和编译器,作为字节码(code object)进行输出。然后字节码再由Python解释器进行运行。这里字节码的作用有点像汇编语言在C语言编译过程。
我们最简单的解释器开始,它只能识别以下三个指令,我们基于一点一点拓展实现我们的整个项目:
我们对7+5生成以下指令集:
1 | byte2exec = { |
之所以通过这种单指令和零指令的方式进行计算,是因为我们的Python解释器实际上是一个基于栈的虚拟机。
我们将指令和数据分开存放,这样保证了指令是定长的。因此,我们也需要向指令指出数据存放的位置,所以一个完整的指令集有两部分,指令和参数位置。对于不需要参数的零指令,我们用None表示。
现在我们可以基于栈来实现一个简单的解释器结构:
1 | class Interpreter: |
现在我们已经实现了一个虚拟机的基本结构和支持的指令,我们需要一个方法来驱动我们的虚拟机进行对指令的解析与执行:
1 | def run(self, code): |
现在我们可以尝试使用它们进行简单的计算3+4+5:
1 | code = { |
可以看到虚拟机按照预期输出了我们想要的结果。
现在我们向虚拟机添加存储功能,我们可以将数值存入变量中,实现变量和值的映射关系,我们将实现以下两个指令:
为了实现这个功能,我们需要再初始化一个内存空间(这里使用字典比较直观),用于存放变量名和值的绑定关系,同时需要在我们的code中添加变量名。我们的实现如下:
1 | class Interpreter: |
这里我们可以试着运行一下x = 3; y = 7; print(x+y):
1 | code = { |
成功的运行了我们的函数。
随着我们支持的指令增多,我们需要不断的通过if-else结构来进行对指令的执行。在我们的实现中,类的方法名和字节码中的指令是相同的,所以我们通过getattr方法来对run()进行优化:
1 | def execute(self, code): |
现在我们可以尝试解析一下真实的Python字节码,我们可以以下面的这个函数为例:
1
2
3
4
5
6def cond():
x = 3
if(x < 5):
return 'yes'
else:
return 'no'
我们可以通过特殊方法__code__获取函数的字节码和元信息,具体的用法如下:
1 | 函数对象 (function) |
这里我们可以通过这个方式得到我们的字节码指令
1 | codebyte = cond.__code__.co_code |
我们得到了这个函数的字节码,但是我们无法阅读它。所以我们需要用到Python中的字节码反汇编器dis,将字节码进行翻译并以可读的形式输出:
1 | import dis |
其中第一列是该指令对应的字节码索引,第二列是该字节码的可读形式,第三列是指令的参数索引(第4列可能会指出使用的是什么参数)
同时我们也可以使用dis库中的opname方法,将对应的字节码翻译成可读的指令:
1 | codebyte = cond.__code__.co_code |
一个语言中条件分支和循环结构的能力也很重要,我们可以借这一段字节码深入的理解Python运行的实现。在我们的例子中if x>5被翻译成了:
1 | 6 LOAD_FAST 0 |
其中LOAD_FAST将局部变量加载到栈上,LOAD_CONST将常数5加载到栈上,然后通过COMPARE_OP指定的比较类型,对栈顶的两个数值进行比较,然后将比较结果放回栈上。最终POP_JUMP_IF_FALSE,根据比较的结果,跳转到指定的指令。跳转后要被加载的指令我们称之为跳转目标,作为POP_JUMP的参数,dis会用>>指出跳转目标。
有了条件判断和跳转之后,我们就可以实现最基本的循环结构,我们对下面这个循环结构进行分析:
1 | def cond(): |
要理解这个循环结构,我们需要从几个跳转指令入手。首先是第一个POP_JUMP,如果判断为真,就进入循环体结构,不为真就直接退出。第二个POP_JUMP则是判断是否退出循环结构。第三个比较特殊JUMP_BACKWARD,它将无条件跳转到循环体的起点。通过跳转和条件分支的功能,实现了循环结构。
其他的语法结构也是类似的,如if ... elif, for ,...,可以通过dis慢慢探索
实现了数值的计算和控制转移之后,现在我们需要进一步认识Python
函数调用的过程。正如上面的那个例子,我们看到RETURN_VALUES,那么结束这个函数之后会返回到哪里呢?
如果我们在函数中,我们会返回到调用者。如果是在模块顶层,我们可能会直接结束程序。我们将上一层的信息返回给下一层,例如在递归调用时,我们还需要保存每一层的局部状态。这就引出了Frame的概念,frame是函数调用的一次执行的上下文。它在python运行的过程中不断的被创建和销毁。
对于一个code object,我们可能会有多个frame。但是对于一个frame,我们有且仅对应一个code object。
frame存在于调用栈之中(和C一样)。Python中有三种类型的栈结构:
在调用栈的每个frame都有它自己的数据栈和块栈。以下面这个程序为例,它在调用栈中的状态大概就是这样的:
1 | >>> def bar(y): |
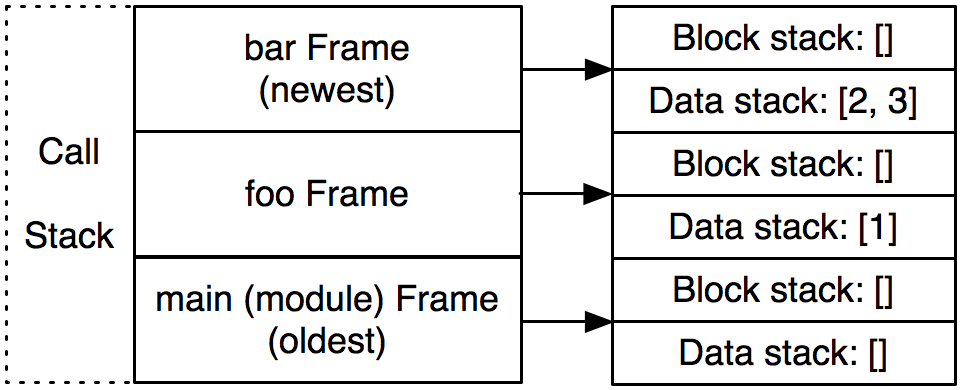
至此,我们对Python字节码的基本分析就结束了
上一章中完成了对图形渲染的饿BVH加速,现在我们要尝试将图片纹理映射到物体中。
图形学中的纹理映射是将材质效果应用于场景中的物理过程。其中”纹理”指的是效果(这个效果可以是材质属性,或是部分存在与否)本身,而映射则是将效果映射到物体的表面上。
最为常见的纹理映射就是将图像映射到物体表面上,就像是把世界地图依附到球体表面。和我们的直觉不同,纹理映射是一个逆向的过程,我们首先确定物体上的一个点,然后查找纹理贴图给定的颜色,以实现对图片的映射。
不过在此之前,我们先用程序化的方式生成纹理颜色,并创建一个纹理贴图。为了执行纹理查找,我们需要物体表面的纹理坐标(u,v)以定位纹理中的像素,同时也需要保存当前点的三维坐标(部分纹理需要这一部分的信息)
我们的纹理颜色类将从最简单的恒定色彩纹理开始实现,实际上我们可以将物体的颜色也视作一种纹理:
1 | #ifndef TEXTURE_H |
这里我们先实现对纹理类的接口的一个实现,然后创建一个恒定色彩纹理类,返回恒定的颜色类型。
注意到我们这里需要使用到(u,v)表面坐标,我们还需要更新hit_record结构,对这些射线碰撞信息进行存储:
1 | class hit_record { |
棋盘纹理作为实体纹理中的一种。实体纹理取决点在空间中的位置,我们可以理解为给空间中的指定点进行着色,而不是给空间中的某个物体上色。正因如此,当我们的物体在空间中移动时,纹理并不会随物体进行移动,反而像是物体在穿过纹理。
这里我们将实现一个棋盘纹理类,它是一种空间纹理(即实体纹理)。根据点在空间中给定的位置进行纹理颜色的渲染。
为了实现棋盘格图案,我们需要对当前点的每个坐标分量取floor,这样我们就将整个空间分割为1x1x1的单元格,每个坐标都可以映射到对应的单元格,我们对奇数的单元格赋予一种颜色,对偶数赋予另外的一种颜色,这样就实现了棋盘的样式。同时我们还可以设置一个缩放因子scale,控制单元格的大小,从而实现对棋盘格的大小控制:
1 | class checker_texture : public texture{ |
为了进一步的支持纹理,我们拓展lambertian类,使用纹理代替颜色:
1 | class lambertian : public material { |
这里通过多态的思想实现了对lambertian材质的纹理的实现。
现在我们可以向我们的场景中添加纹理了:
1 | // main.cpp中将地面设置成棋盘样式 |
渲染结果如下:
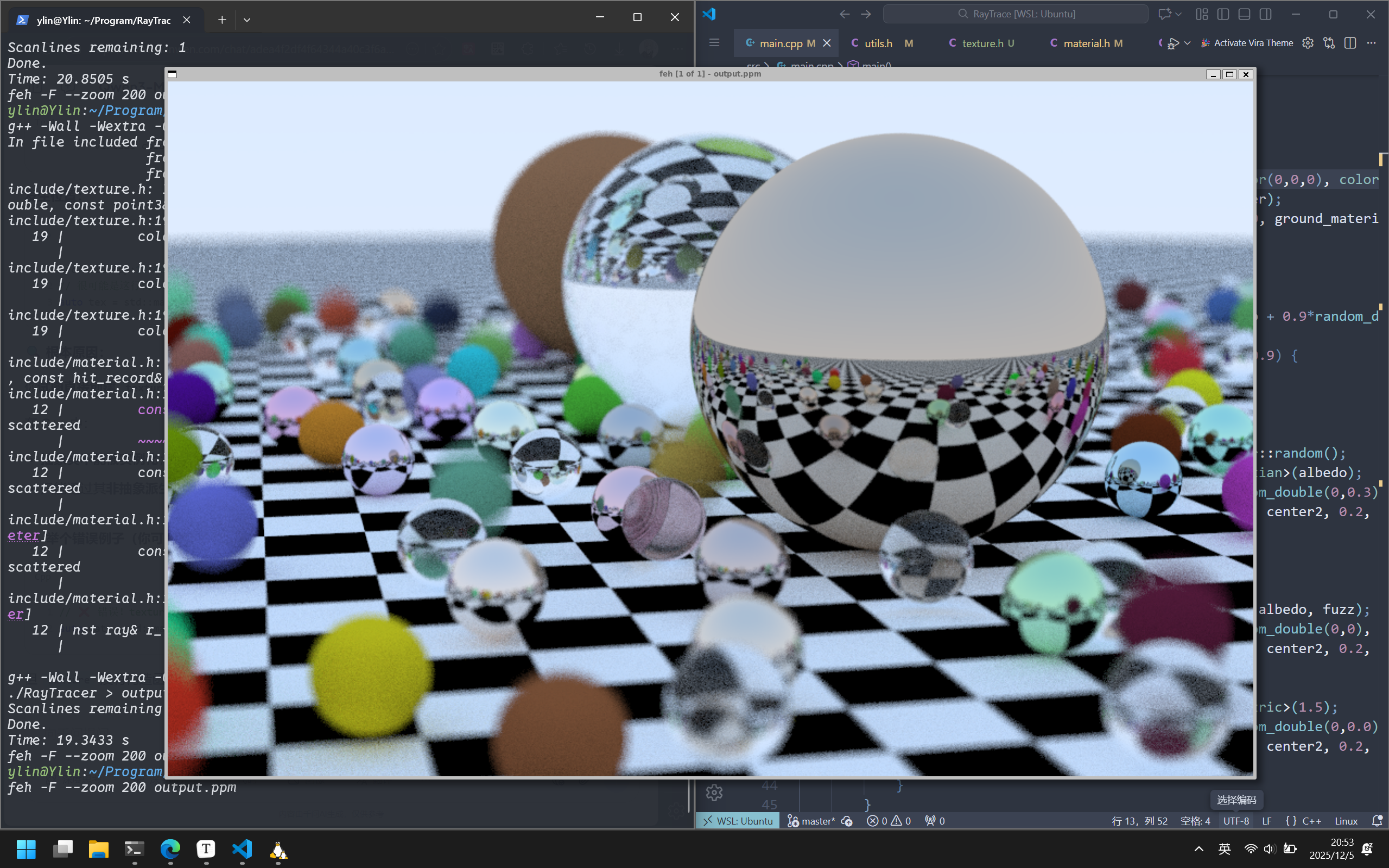
正如之前所提到的,这种实体纹理的上色方式,更像是物体在穿过纹理,从而完成上色。
我们现在创建一个新的场景来观察这种特殊的情况,我们将先前的main函数保存为一个bounding_ball场景,然后现在我们再来创建一个新的场景:
1 | void checkered_spheres() { |
我们通过main函数中的switch来切换我们想要渲染的场景:
1 | int main(){ |
我们渲染出来的结果如下:
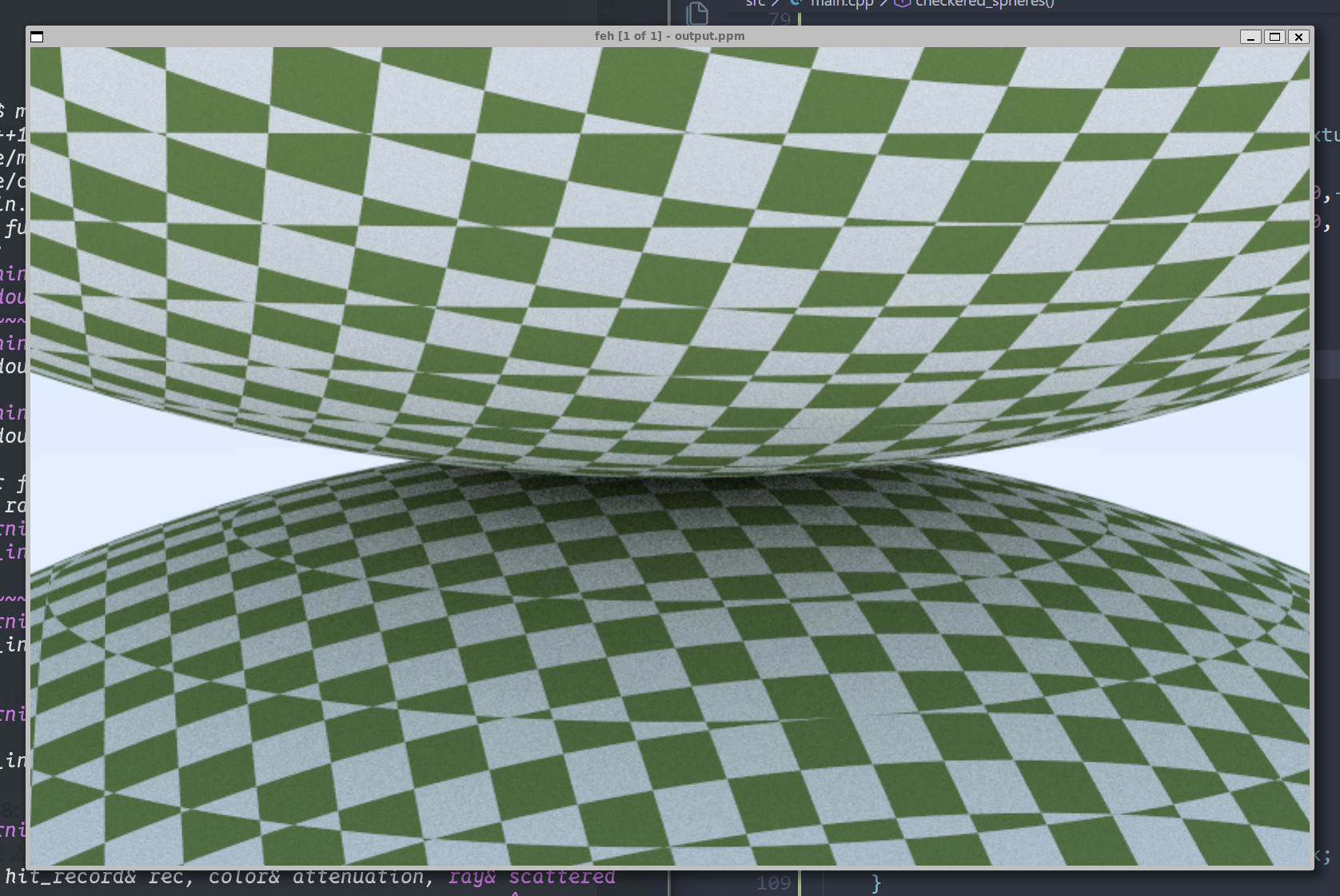
这就是空间纹理渲染的特殊情况,不过你应该能理解这是什么情况。所以为了解决这个问题,我们需要使用表面纹理,这就意味着我们需要根据(u,v)的球体表面位置信息来创建纹理。
空间纹理通过空间中一点的坐标,实现纹理的绘制。但是真如我们先前所提到的空间纹理的局限性,我们希望能够更具球体表面的坐标实现对图像点对点的映射。这就以为着我们需要一种方法来查找三维球体表面任意点的坐标(u,v)。
这里用到一个经纬度的思想,首先确定出这个点在球体上的经纬度(θ, ϕ)(横纬竖经,这里θ从-Y向上,ϕ从-X到+Z到+X到-Z),然后再将球面坐标表示出来,这里的话,如果学过球面坐标,自然能够得到以下式子:
$$ 我们可以简单的推导得到:
$$
所以我们可以写出sphere类中的get_uv方法:
1 | static void get_uv(const point3& p, double& u, double& v){ |
然后我们向hit方法中添加,每次碰撞记录的(u,v):
1 | bool hit(const ray& r, interval t_range, hit_record& rec) const override { |
现在我们就实现了对球体表面的位置的(u,v)二维定位
现在我们需要一种手段,将图片数据解析为一种二维关系,我们希望通过(u,v)访问图像数据上对应的像素值。所以我们需要将图片加载为一个浮点数数组,便于我们访问。这里我们使用第三方库stb_image.h来实现
首先我们创建一个辅助类来帮助我们管理图片信息内容,以提供一个pixel_data(int x,int y)方法,来访问任意像素的8位(unsigned
char)RGB。
我们的实现如下:
1 | #ifndef IMAGE_H |
现在我们封装好了一个加载并获取图像内容的image类,我们可以利用它实现图像纹理image_texture:
1 |
|
现在我们可以尝试将一个图片进行渲染:
1 | void earth() { |
我们使用一张地球的贴图(效果如下):
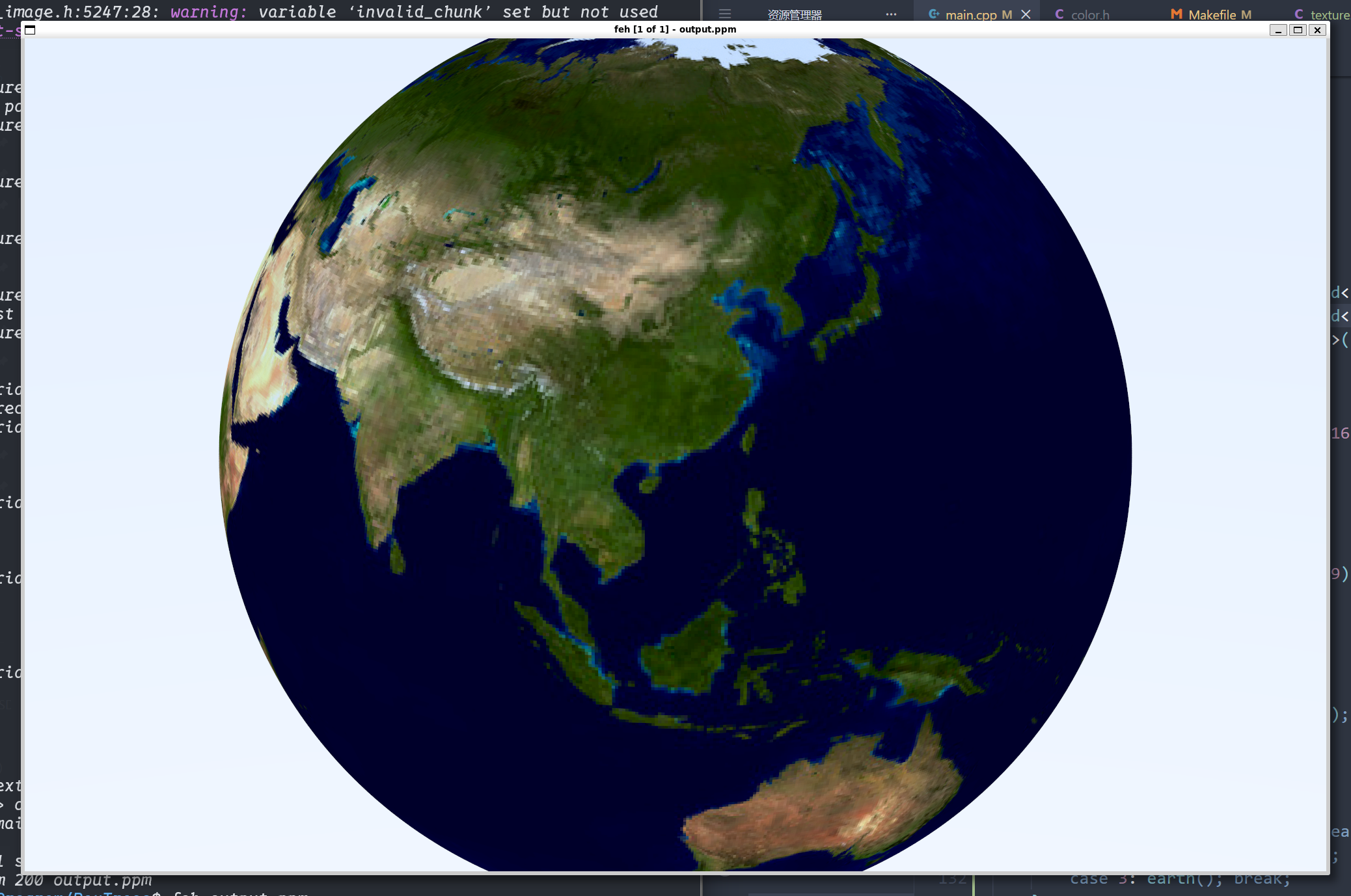
至此 我们的纹理样式就简单介绍完了
书接上回,上一次实现了物体运动下的图形学渲染。实现了动态模糊的构建。
现在随着我们场景的复杂化,和对图片质量的提升,有时候渲染一张照片都需要十几分钟。为了让代码运行的更快,我们需要引入一个新的结构 包围体积层级BVH,以优化程序渲染的性能。
射线 - 对象求交,是光线追踪过程中的主要性能瓶颈,运行的时间和物体的数量呈线性关系。每当我们发射一条射线,就需要对场景内的所有物体进行求交判断。但是实际上和很多物体的求交是没有必要的,我们向天空发射的一条光线并不会和地上的物体有所交集。
所以我们为了优化这个过程,我们需要避免不必要的射线 - 对象求交计算,接下来我们要学习的方法就是通过包围体积层次来实现对求交场景的优化。
为一组对象创建一个完全包围所有对象的包围盒,假如射线会错过这个包围盒,那么它一定会错过这个包围盒中的所有物体,反之,则有可能击中盒中的任意一个对象,所以我们的思想如下:
1 | if(ray hits bounding object) |
为了提高计算的效率,使得处理时间的增长速度慢于物体数量的增长。首先我们需要构建有一个层次化的包围体结构,这里我们通过自顶向下的方法,生成我们的包围体积的层级结构。
一开始我们需要构建一个层次化的包围体结构,用大的包围体包住一群物体,再逐层细化,就像下面这样:
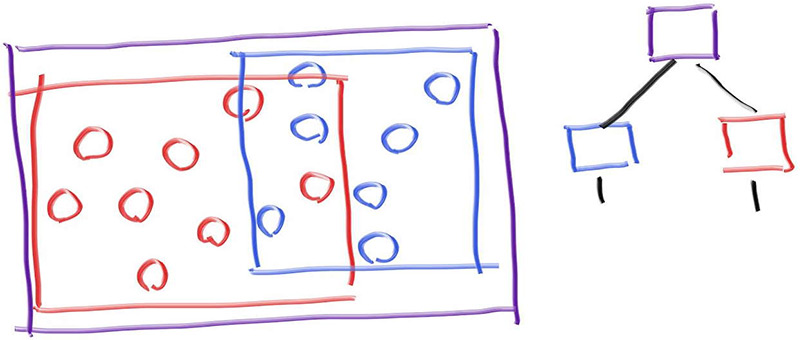
我们可以写出以下伪代码:
1 | if(hit purple) |
当我们确定击中紫色包围盒时,分别对里面的蓝色组和红色组进行分析,从而进一步缩小碰撞检测的范围
要让整个层次结构高效工作,我们需要要一个好的划分方式,而且我们需要一个较快的检测光线和包围体相交的算法,否则我们检测相交的速度会抵消掉包围结构层次带来的加速效果。这里我们选择轴对齐包围盒作为我们的包围体。我们通常将其称为AABB。
接下来我们需要了解光线和AABB相交检测的slab方法:
首先我们需要知道什么是片层(Slab),片层是在一个坐标轴方向上,由两个平行平面围成的空间区域,比如在
x 轴方向,若 AABB 的 x 范围是 [x_min, x_max],那么这个 slab 就是所有满足
x_min ≤ x ≤ x_max
的点。在我们要用到的3D场景中,AABB = x-slab && y-slab && z-slab。
理解片层之后,我们检测碰撞的关键就在于计算光线和不同片层之间的交点,其中射线的函数定于为P(t) = Q + td,我们可以求出其在x = x0t平面的交点为: $$ \begin{align*} x_0 &= Q_x + t_0d_x \\ t_0 &= \frac{x_0 - Q_x}{d_x} \\ t_1 &= \frac{x_1 - Q_x}{d_x} \end{align*} $$ 知道光线与各个片层之间的交点之后,我们可以进一步判断光线和AABB的相交情况了,以下图为例:
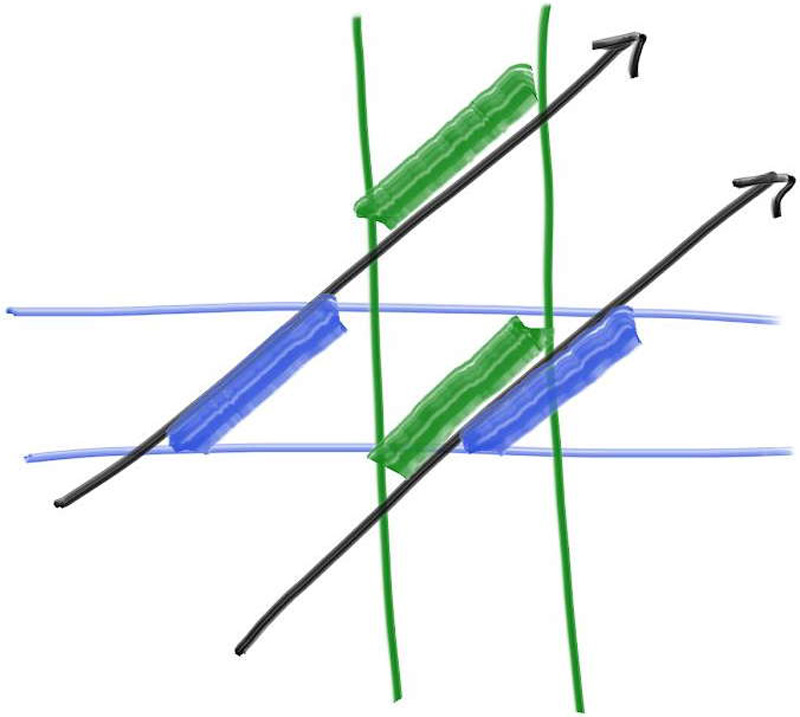
这是一个二维的AABB场景,上面的射线和x、y片层中的交集段并没有重叠,所以我们知道射线并没有和AABB发生交集,下面的射线和x、y片层的交集段发生了重叠,所以说射线和AABB之间是有交集的。
上图我们可以用于以下伪代码确定射线是否和AABB发生碰撞:
1 | interval_x <- compute_intersection_x(ray, x0, x1) |
相应的三维版本如下:
1 | interval_x <- compute_intersection_x(ray, x0, x1) |
我们已经知道了怎么求出射线和片层的相交区间,我们需要进一步的检测这些相交区间是否有交集,现在,我们的关键在于实现overlaps了,在此之前我们需要考虑以下几种特殊情况:
min和max来标识我们的区间-infinity/+infinity,我们通过min/max可以解决这个问题现在我们可以写出伪函数overlaps:
1 | bool overlaps(t_interval1, t_interval2) |
对于第三种特殊情况,此时我们无法给出准确的t_min和t_max,所以我们将这个情况称之为NaN,这里我们需要进行手动的处理,为区间添加一个padding,将NaN的情况视作fasle
为此我们需要为interval添加一个expend函数,它给区间填充给定的值:
1 | class interval { |
现在,我们可以开始实现AABB类了:
1 | #ifndef AABB_H |
这里的关键在于hit函数,我们通过区间收缩的方式实现对交集的判断。
现在我们需要为所有的可击中类构建一个包围盒,对于单个的物体,我们将其包围盒视作包围结构层次中的叶子节点,这个我们之后会提到。
由于我们的物体有部分是动画的,所以我们为其生成的包围盒边界应该等于其运动范围,首先,我们需要升级我们的hittable类:
1 | class hittable{ |
对于静态和动态的球体,我们很容易为其创建出包围盒:
1 | class sphere: public hittable { |
这里注意到我们直接将box1和box2合并成了一个新的包围盒区间,这是我们新定义的一种构造方法,也便于之后的包围盒合并:
1 | aabb(const aabb& box1, const aabb& box2){ |
现在我们需要更新对象列表hittable_list,现在列表中的物体被创建时,会生成相应的包围盒边界。而我们需要随着每个新子节点的加入逐步的更新边界框,于是我们有:
1 | class hittable_list : public hittable { |
BVH本质上也是一个hittable
,它代表一组几何体,光线可以击中它以进行相交判断。我们将它视作一个对象的容器,它封装了几何体,通过包围盒相交测试进行加速检测。
我们通过一个类来实现它,它既可以是节点,也可以是整棵树的根:
1 | #ifndef BVH_H |
接下来的重点在于怎么将hittable_list构建成我们想要的BVH。我们希望每个BVH下至多有两个左右节点,但是我们以什么为依据进行划分呢,以下是我们的做法:
当我们构建BVH的递归生成时,会有以下几种情况:
因此,我们的BVH生成的算法如下:
1 | bvh_node(std::vector<shared_ptr<hittable>>& objects, size_t start, size_t end) { |
这里sort使用的判断逻辑如下:
1 | static bool box_compare( |
不过实际上我们是可以对这一部分优化的。我们希望构造出来的BVH树是均衡的,所以每次对场景内的物体进行划分时,我们希望,左右子树的分布是均衡的,这就要求我们每次选择的检测轴应该是边长最长的轴。为此我们需要一个函数为我们计算出包围盒的范围,我们将以此为依据实现更加平衡的BVH树结构:
1 | bvh_node(std::vector<shared_ptr<hittable>>& objects, size_t start, size_t end) { |
为了实现对最长轴的判断 和
包围盒并集的实现,我们需要优化我们的aabb类:
1 | class aabb{ |
至此我们就实现了图形的加速渲染。太爽了。
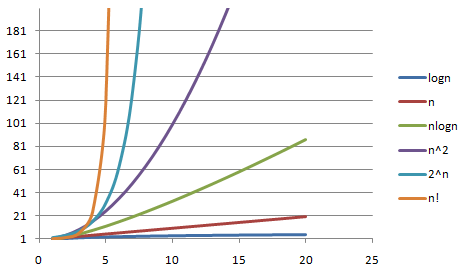
速度差不多提升3-4倍,随着场景规模的提升,这个提升的效果更加明显,可以借下面这个图来感受一下。我们差不多实现了从O(n)到O(logn)的优化: